Тема 10. ИНДЕКСЫ
В данной теме рассмотрены виды, особенности и назначение таких статистических показателей, как индексы. Представлен в общем виде алгоритм факторно-индексного анализа, а также особенности его применения для изучения динамики средней величины.
1. Понятие и назначение индексов. Виды индексов.
2. Факторно-индексный анализ.
3. Факторно-индексный анализ динамики средней величины.
Понятие и назначение индексов. Виды индексов
Индекс – показатель сравнения двух состояний одного и того же процесса или явления.
Примеры:
– цепной темп роста показателя «Выбросы в атмосферу загрязняющих веществ» в 2002 году по Челябинской области составил 0,918; этот показатель является индексом, сопоставляющим значения двух состояний (2002 и 2001 годы) одного и того же процесса или явления (показателя «Выбросы в атмосферу загрязняющих веществ» по Челябинской области):
– отношение объема выбросов в 2002 году по Челябинской области к аналогичному показателю по Свердловской области составляет 0,740; этот показатель является индексом, сопоставляющим значения двух состояний (в Челябинской области и в Свердловской области) одного и того же процесса или явления (показателя «Выбросы в атмосферу загрязняющих веществ» в 2002 году):
;
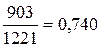– отношение объема выбросов в 2002 году по Челябинской области к средней по РФ величине составляет 4,086; этот показатель является индексом, сопоставляющим значения двух состояний (в Челябинской области и в среднем по РФ) одного и того же процесса или явления (показателя «Выбросы в атмосферу загрязняющих веществ» в 2002 году):
.
Основное назначение индексов – это сравнение явлений во времени, в пространстве и с нормативами (средними), а также анализ изменения явлений по факторам.
Различают следующие виды индексов: 1) базисные и цепные; 2) индивидуальные, сводные, агрегатные.
Рассмотрим подробнее первую группировку. Базисные и цепные индексы различаются базой сравнения: первые сопоставляют изучаемое состояние явления с предшествующим, а вторые – с некоторым, выбранным за базу для сравнения. И те и другие индексы могут оценивать изменения как во времени, так и в пространстве. Примерами базисных и цепных индексов сопоставления значений показателей во времени могут служить базисные и цепные темпы роста показателей (см. 9.2. «Ряды динамики»). Базисные и цепные индексы сопоставления значений показателей в пространстве – это соотношения характеристик объектов в ранжированном ряду (соответственно с первым в ряду значением и с предыдущим). Индексы показывают, во сколько раз данное значение превышает значение единицы, принятой за базу, или значение предыдущей в ряду единицы.
Пример 1. В ранжированном (по возрастанию признака) ряду 89 административно-территориальных единиц Российской Федерации по признаку «Выбросы в атмосферу загрязняющих веществ» в 2002 году на первом месте находится Кабардино-Балкарская республика со значением признака 1 тыс. т (минимальное значение в ряду). Челябинская область (со значением 903 тыс. т) в этом ряду непосредственно следует за Ямало-Ненецким автономным округом (со значением 725 тыс. т). Таким образом, базисный и цепной индексы для показателя Челябинской области равны соответственно 903 и 1,25:
; 
.
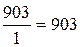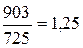Пример 2. Ежегодно студенты V курса факультета «Экономика и управление» сдают государственный экзамен по специальности. Экзамен представляет собой тест из заданий по разным дисциплинам финансово-экономического блока. По результатам экзамена определяются рейтинги студентов в соответствии с количеством набранных ими баллов (процентом правильно выполненных заданий). По формируемым спискам можно подсчитать отставание конкретного студента от предыдущего в списке (цепной индекс) и от лучшего в списке (базисный индекс). Например, по данным представленного списка результат Санниковой О. на 28,6 % слабее лучшего в группе и на 6,2 % отстает от предыдущего.
Результаты государственного экзамена по специальности
1. Кузьмина К. – 5 (84 %).
2. Антонова М. – 5 (76 %).
3. Реутова Ю. – 5 (76 %).
4. Чернышев Е. – 5(75 %).
5. Ясина О. – 5 (75 %).
6. Аверченко В. – 4 (70 %).
7. Коновалова В. – 4 (64 %).
8. Санникова О. – 4 (60 %);
базисный индекс: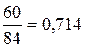 
; цепной индекс: 
.
9. Яровой Д. – 4 (60 %).
10. Ипатов А. – 4 (60 %).
11. Зайцев Е. – 4 (60 %).
Для более подробного изучения индексов введем следующие обозначения:
| i | – | индивидуальный индекс; |
| I | – | агрегатный (сводный) индекс; |
| p 0 | – | цена продукции в базисном периоде; |
| p 1 | – | цена продукции в отчетном периоде; |
| q 0 | – | объем отдельного вида продукции в базисном периоде; |
| q 1 | – | объем отдельного вида продукции в отчетном периоде; |
| Q 0 | – | суммарный (по видам, способам или каналам продаж и т. д.) объем продукции в базисном периоде; |
| Q 1 | – | суммарный (по видам, способам или каналам продаж и т. д.) объем продукции в отчетном периоде; |
| dq 0 | – | доля отдельного вида (или выделенной по какому-либо признаку части) продукции в общем объеме в базисном периоде; |
| dq 1 | – | доля отдельного вида (или выделенной по какому-либо признаку части) продукции в общем объеме в отчетном периоде; |
| z 0 | – | себестоимость единицы продукции в базисном периоде; |
| z 1 | – | себестоимость единицы продукции в отчетном периоде; |
| R 0 | – | рентабельность продукции в базисном периоде; |
| R 1 | – | рентабельность продукции в отчетном периоде; |
| P 0 | – | прибыль в базисном периоде; |
| P 1 | – | прибыль в отчетном периоде. |
Индивидуальный индекс – это результат сопоставления характеристик отдельных единиц статистической совокупности. Сводный индекс – это результат сопоставления обобщенных характеристик явления по группам единиц. Агрегатный индекс – это результат сопоставления обобщенных характеристик явления по группам единиц, приведенных к обобщенному виду путем взвешивания.
Примеры индивидуальных, сводных и агрегатных индексов:
– все рассмотренные выше индексы – индивидуальные (сопоставляются характеристики одного или отдельных регионов, одного или отдельных студентов);
– индивидуальные индексы цены отдельного товара в разные периоды времени:
;
где первая цифра индекса обозначает номер периода: 0, 1; вторая – номер товара: 1, 2, …, n;
– сводный индекс: соотношение суммарной по всем регионам величины выбросов в атмосферу в 2003 году к аналогичной характеристике 2002 года;
– агрегатные индексы цены:
· индекс Ласпейерса (1864 г.)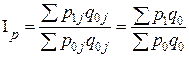 
;
(для удобства работы с данными вторую цифру индекса, указывающую номер единицы совокупности, как правило, опускают);
· индекс Пааше (1874 г.)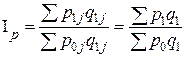 
;
– агрегатный индекс физического объема:
;
– сводный индекс стоимости:
Значения базисных и индивидуальных индексов связаны следующим соотношением:
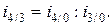
Данные соотношения можно использовать либо для выполнения, либо для проверки расчетов.
Факторно-индексный анализ
Факторно-индексный анализ – это метод измерения влияния изменения значений отдельных факторных признаков на изменение значений результативного признака.
Процедура факторно-индексного анализа включает в себя следующие 5 этапов:
1. Построение формулы, определяющей зависимость результативного признака и факторных признаков:
.
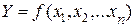Например: показатель суммы прибыли от производства и реализации продукции может быть представлен как функция 4 переменных: цены на продукцию (p), себестоимости продукции (z), структуры реализации продукции (dq), объема реализации (Q):
,
или 
.
2. Определение последовательности подстановок:
x 1 – x 2 – … – xn.
В отечественной практике принято начинать подстановки с количественных факторов, поэтому последовательность подстановок для показателя «сумма прибыли» начинается с показателя объема:
Q – dq – z – p.
3. Расчет общего относительного и общего абсолютного изменения.
Общий индекс и абсолютное изменение отражают изменение индексируемого показателя под влиянием всех факторов соответственно в относительном и абсолютном выражении:
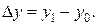
4. Расчет частных относительных и частных абсолютных изменений.
Частные индексы и частные абсолютные изменения показывают, как изменилось значение индексируемого показателя под влиянием одного отдельно взятого фактора. Расчет выделенного влияния одного из факторов достигается за счет того, что в формуле частного индекса значение фактора, влияние которого измеряется, представлено разными периодами в числителе и знаменателе. Таким образом, числитель отражает такое значение изучаемого признака, которое имело бы место при значении факторного признака отчетного периода, а знаменатель – значение изучаемого признака, которое имело бы место при условии, что значение факторного признака такое же по величине, как в базисном периоде, при прочих равных условиях:
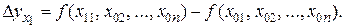
Например, частный индекс влияния фактора объема реализации на величину объема прибыли показывает, во сколько раз увеличилась бы сумма прибыли в отчетном году при условии, что объем реализации продукции в отчетном году был бы таким, как в отчетном году, а цена, себестоимость и структура выпуска остались бы такими же, как в базисном, и рассчитывается по формуле
или 
при этом частное абсолютное изменение рассчитывается по формуле
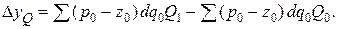
Аналогично рассчитывают частные изменения по всем другим факторам.
…
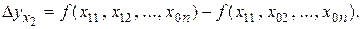
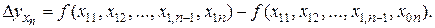
5. Проверка соотношений общего и частных изменений:
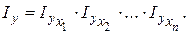
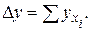
Примечание. По этому же алгоритму можно проводить факторный анализ на основе уравнения регрессии. Различие будет состоять лишь в том, что анализу подвергаются признаки, связанные корреляционно, поэтому и рассчитанное влияние будет носить вероятностный характер.
Пример. Определить, как повлияло на изменение объема производства за год изменение производительности труда и численности.
Таблица 10.1
Показатели деятельности предприятия
| Показатели | Обозначение | 2002 г. (0) | 2003 г. (1) |
| Объем производства, тыс. шт. | Q | ||
| Численность, чел. | T | ||
| Производительность труда, тыс. шт./чел. | W |
Решение.
1) Запишем формулу, определяющую зависимость результативного признака и факторных признаков:
Q = WT.
2) Определим последовательность подстановок: T – W.
3) Рассчитаем общее относительное и общее абсолютное изменения:
; 
Объем производства за год увеличился в целом (под влиянием всех факторов) в 1,5 раза, или на 100 тыс. шт.
4) Рассчитаем частные относительные и абсолютные изменения.
4.1. Частный индекс и частное абсолютное изменение в результате влияния динамики численности на объем производства:
; 
За счет сокращения численности работающих объем производства за год уменьшился в 2 раза, или на 100 тыс. шт.
4.2. Частный индекс и частное абсолютное изменение в результате влияния динамики производительности труда на объем производства:
; 
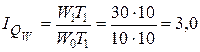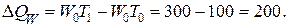
За счет роста производительности труда объем производства за год увеличился в 3 раза, или на 200 тыс. шт.
5) Проверим соотношение общего и частных изменений:
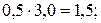– 100 + 200 = 100.
Выводы. Общее изменение объема производства продукции за год составило +100 тыс. шт. (увеличение на 50 %), при этом за счет показателя производительности труда изменение составило +200 тыс. шт. (увеличение на 200 %) и за счет показателя численности – –100 тыс. шт. (уменьшение на 50 %).
