Определение определённого интеграла

Экстремумы функции двух переменных.

Определение. - точка минимума (максимума функции z = f (x, y), если 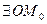такая, что для 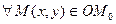при .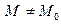

 

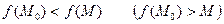Рисунок. Необходимое условие существования экстремума

функции z = f (x, y) в точке :

или в точке частные производные (возможно, одна из них) не существуют.

 

 

Доказательство. Пусть - точка экстремума. Рассмотрим функцию 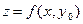от одной переменной х. При эта функция имеет экстремум, поэтому по Т.Ферма её производная при равна 0 или не существует.

Поэтому или не существует.

Теперь рассмотрим функцию от одной переменной y. При она имеет экстремум, поэтому её производная или не существует.

 

Пример. Найдём точки, в которых функция может иметь экстремумы.

Получим систему уравнений

Решение этой системы определяет точку , в которой может существовать экстремум исследуемой функции.

 

Неопределённый интеграл

Задача. Дана функция f (x). Найти функцию F (x): .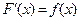

 

Определение. Функция F (x) называется первообразной от функции f (x) на (a, b),если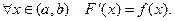

 

Пример. f (x) = 2 х.

 

Теорема. Пусть - первообразные от f (x) на (a, b). Тогда на (a, b)

 

Доказательство (нестрогое). Рассмотрим функцию . Hа (a, b). Поэтому φ (х) не возрастает и не убывает на (a, b) =>

.

 

Следствие. Если F (x) - одна из первообразных от f (x), то любая первообразная от f (x) имеет вид F (x) + С, где .

 

Определение. Множество всех первообразных от функции f (x) называется неопределённым интегралом от функции f (x): если то = F (x) + С,

 

Как находить неопределённый интеграл?

 

I. Таблица неопределённых интегралов.

II. Свойства неопределённого интеграла.

1.

2.

3.

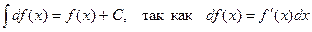
4.

5.

 

III. Общие методы интегрирования

 

1. Подведение под знак дифференциала

 

 

Примеры.

,

 

 

2. Замена переменной интегрирования (метод подстановки)

 

Примеры.

 

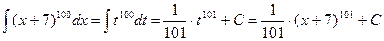
t=x+ 7 x=t- 7 dx = dt

 

3. Интегрирование по частям

 

Пусть u (x), v (x) - дифференцируемые функции. Тогда

 

Доказательство.

=>

 

(= uv)

 

Пример.

 

 

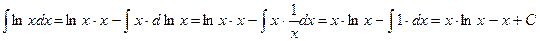
Определённый интеграл

Задача определения площади S криволинейной трапеции.

Пусть f (x) непрерывна на [ a, b ], f (x) > 0 для Как определить S? Исходное понятие – площадь прямоугольника.

 

Рисунок 1.

 

Приблизим криволинейную трапецию ступенчатой фигурой из прямоугольников.

Для этого разобьём [ a, b ] на n отрезков точками

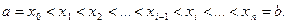
Для каждого обозначим его длину .

В каждом отрезке возьмём произвольную точку Тогда - площадь прямоугольника с основанием .

Площадь S (n) ступенчатой фигуры, которая приближает криволинейную трапецию, равна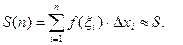

С возрастанием n при , ступенчатая фигура всë лучше (точнее) приближает криволинейную трапецию, поэтому

 

 

Аналогия из школьной математики: по определению площадь круга –это предел последовательности площадей вписанных в него правильных многоугольников при бесконечном удвоении числа его сторон.

 

Определение определённого интеграла

 

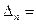
Пусть функция f (x) непрерывна на -разбиение отрезка [ a, b ] на n отрезков длины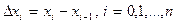

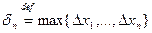- диаметр разбиения ,

 

- интегральная сумма разбиения .

 

Для непрерывной функции f (x) существует предел последовательности интегральных сумм при n → ∞ и

 

число, не функция!