Основы статистического анализа результатов измерений партии деталей

Все детали в партии отличаются друг от друга своими фак­тическими размерами (или другими показателями качества). Го­ворят: "Имеет место разброс или рассеяние параметров". Поэ­тому размер детали выступает как случайная величина. Хапактер рассеяния размеров деталей в партии устанавливают построением практической (эмпирической) кривой распределения. При этом используется выборочный метод для определения количества и последовательности отбора деталей из партии для измерения.

Все изготавливаемые детали принадлежат к некоторой сово­купности деталей, которые можно было бы получить, если про­должать ТП очень долго без изменения его режимов и условий. Будем называть их объектами. Эти объекты составляют гене­ральную совокупность. Из нее извлекают (некоторым образом) п объектов. Число п называют объемом выборки. Эту выборку подвергают анализу и по его результатам описывают всю гене­ральную совокупность или какие-то ее характеристики с той или иной достоверностью. По объему выборки могут быть очень малыми (п < 10), для которых можно определить только чис­ловые параметры распределения, малыми (10 < n < 30) и боль­шими (n > 30). Объем п > 250 уже не приводит к повышению достоверности оценки.

Практическую (эмпирическую) кривую распределения строят вначале с помощью так называемых гистограммы и полигона распределения (дифференциальных и/или интегральных). Для оценки степени совпадения теоретических и практических за­конов распределения используют те или иные критерии согласия. После установления закона распределения находят, оценки его параметров (выборочные параметры). Оценки числовых харак­теристик (выборочные математическое ожидание, дисперсия, мо­менты) можно определять и без установления закона распреде­ления. Найденные законы и числовые оценки затем используют для анализа параметров ТП и других целей.

26. Построение гистограмм и полигонов распределения

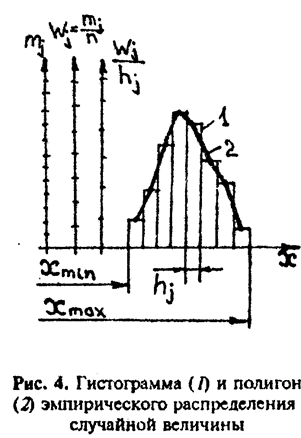
Исходными данными являются наблюдаемые, т.е. опытные значения х₁,х₂,..., x_n случайной величины X. Эти значения рас­полагают в возрастающем порядке (получают так называемый вариационный ряд). Затем весь интервал изменения данных вы­борки (размах выборки) разбивают на разряды или варианты (узкие интервалы длиной h_j, не обязательно равновеликие). Их

число колеблется от 10 до 20. Подсчитывают число ту (частоту) значений x_i, попавших в каждый разряд, а потом для каждого разряда вычисляют относительную частоту (или частость) Wj = m_j/n.

С их помощью строят гистограмму распределения. Для этого на оси абсцисс в выбранном масштабе откладывают разряды h_j (интервалы) и на каждом, как на основании, строят прямоугольник высотой с_j= W_j/h_j, которая харак­теризует плотность относительных частот. Площадь j-го прямоуголь­ника равна h_j • W_j/h_j = W_j. значит равна

площадь всей гистограммы

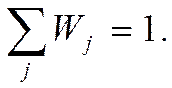
Если на серединах разрядов по­строить ординаты, пропорциональ­ные частотам m_j, соединить их концы отрезками, то можно полу­чить фигуру, называемую полиго­ном распределения, который дает приближенное представление о виде кривой распределения (рис. 4).

27. Оценки числовых характеристик случайных величии

Наиболее употребимыми оценками являются:

1) поле рассеяния w:

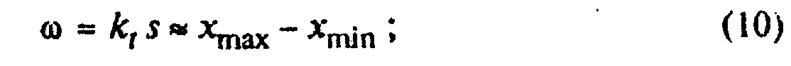
2) среднее арифметическое или центр группирования откло­нений х:

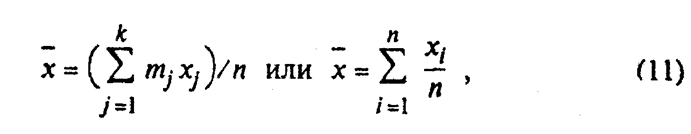
где k — число разрядов, x_j — значение х, на середине интервала.

х часто называют выборочным средним. Оно является оцен­кой математического ожидания генеральной совокупности. Ясно, что если извлекать другие выборки, т.е. брать другие партии деталей, то у них будут свои значения среднего. Значит, среднее арифметическое можно рассматривать как случайную величину со своим распределением и своей дисперсией.

3) выборочная дисперсия s²:

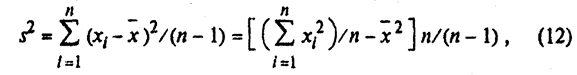
4) выборочное среднее квадратическое отклонение (от центра группирования) s.

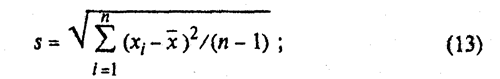
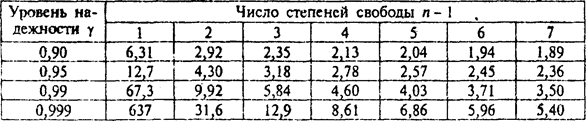
5) доверительный интервал для оценки неизвестного (теоре­тического) параметра 9. Это интервал (q^* - d, q^* + d), в который неизвестный параметр 9 попадает с заданной точностью S при заданной надежности g (доверительной вероятности), где q^* — выборочная оценка для 9. В частности, для нормального рас­пределения с математическим ожиданием т_x = a₀ при неизвест­ном s и малой выборке доверительный интервал определяется как х - t_g s < а₀ < х + t_g s, где t— коэффициент Стьюдента (табл. 1).

Таблица 1

Значения коэффициента Стьюдента t_g