Основы статистической обработки результатов измерений отдельных деталей

13. Исходные термины и определения

Измерение — нахождение значения физической величины опытным путем с помощью специальных технических средств. Количественное содержание какого-либо свойства в объекте яв­ляется размером физической величины, а числовую оценку ее размера называют значением физической величины.

Средство измерения — техническое средство, используемое при измерениях и имеющее нормированные метрологические свойства (например, меры, измерительные приборы, преобразо­ватели).

Мера — средство измерений, предназначенное для воспро­изводства физической величины заданного размера (например, гиря — мера массы N-го размера).

14. Способы измерений

Измерением узнают, во сколько раз значение данной вели­чины отличается от значения величины, принятой за единицу. По способу получения числового значения измеряемой величины все измерения делят на прямые, косвенные (а также совокупные и совместные).

Прямые измерения — такие, при которых искомое значение величины находят непосредственно из опытных данных.

Косвенные измерения - такие, при которых результат опре­деляют на основании прямых измерений величин, связанных с измеряемой величиной (Z) известной зависимостью

Z = f(X,X₁,…,X_n).

15. Методы измерений

Под методом измерений понимают совокупность приемов ис­пользования принципов и средств измерения. Для прямых из­мерений различают следующие методы: непосредственной оцен­ки, сравнения с мерой, дифференциальный, нулевой, совпадений (нониусный), замещения.

Контроль — это измерение, в процессе которого определяют, находится ли значение измеряемой величины в заданных пре­делах, но без отыскания ее численного значения.

Погрешность измерения — отклонение результата измерения от истинного (действительного) значения измеряемой величины. Она порождается множеством причин, например погрешностью настройки средств измерения, погрешностью получения, преоб­разования и выдачи информации в измерительной цепи, изме­нением внешних условий (температура, влажность и др.), ква­лификацией оператора и др.

Абсолютная погрешность измерений выражается в единицах измеряемой величины как разность истинного и наблюдаемого значений измеряемой величины

Относительная погрешность — это отношение абсолютной по­грешности к истинному значению.

В зависимости от характера проявления и причин возник­новения при измерениях различают систематическую и случай­ную составляющие погрешности измерения и грубые погреш­ности или промахи. Промах сразу исключают из результатов из­мерений (наблюдении).

 

16. Основные правила обработки результатов прямых измерений

Обработка результатов прямых измерений. В основе методик оценки результатов измерения лежит понятие о законах распре­деления вероятности случайных величин. Пусть мы провели п прямых измерений некоторой физической величины, истинное значение которой (нам неизвестное) обозначим через а. Появ­ление некоторого значения а_i в процессе измерения является случайным событием. Вероятность появления этого значения в интервале da определяется законом Гаусса.

В условиях производства, как правило, выполняют какое-то ограниченное число измерений (п < 10). Поэтому при анализе результатов измерений используют выборочное среднее а и вы­борочную дисперсию s², которые вычисляют как

Корень квадратный из выборочной дисперсии s² определяет среднюю квадратическую погрешность отдельного измерения s.

По результатам выборок и по их объему можно лишь уста­новить границы (доверительный интервал), внутри которых с определенной (заданной) вероятностью будет находиться истин­ное значение а измеряемой величины. При нормальном распре­делении для математического ожидания доверительный интервал, в который должно попадать истинное значение а, будет равен M(a)± k_gs_a^_, где s_a^_ — среднее квадратическое отклонение рас­пределения средних значений с; разных выборок; k_g — некоторый коэффициент, зависящий от надежности g.

При малом объеме выборки (при измерениях число повтор­ных измерений обычно равно 5...7) оценкой для о будет средняя квадратическая погрешность результата серии измерений s_a^_. (го­ворят "ошибка среднего"), которая вычисляется по формуле

При этом коэффициент k_g заменяют на коэффициент Стьюдента t_g, значения которого подчиняются распределению Отьюдента и зависят от значения п - 1 и доверительной вероятности у. Некоторые значения, коэффициента t_g приведены в табл. 1.

На основе вышеизложенного обработку результатов прямых измерений рекомендуется проводить следующим образом:

1. Записать результаты каждого измерения а,- в таблицу.

2. Вычислить среднее значение из п измерений по формуле

3. Вычислить погрешности отдельных измерений D a_i:

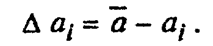
4. Вычислить квадраты погрешностей отдельных измерений D a_i².

5. Если один-два результата сильно отличаются от остальных, то следует проверить, не являются ли они промахом, который следует исключить.

6. Определить среднюю квадратическую погрешность резуль­тата серии измерений S_a^_ (ошибку среднего):

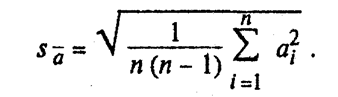
7. Задать уровень надежности g (обычно g = 0,9 или 0,95).

8. Определить по справочным таблицам коэффициент Стью­дента t_g для принятой надежности и числа проведенных изме­рений п.

9. Определить ширину доверительного интервала (погреш­ность результата измерения) D а:

10. Окончательный результат измерений записать в виде

 

17. Обработка результатов косвенных измерений.

Если искомая величина Z является известной функцией некоторых величин a,

B, с и т.д., т.е. Z= f (a, Ь, с,...), которые сами определяются пря­мыми измерениями, то величину Z находят двумя способами а зависимости от числа наблюдений для величин а, b, с,....

1-й способ. Если число этих наблюдений (серия измерений) не превышает 20 для каждой из этих величин (необязательно одинаковое число), то порядок определения величины Z будет следующим.

1. Для каждой серии измерений величин a, b, с,.., входящих в определение искомой величины Z, находят средние значения `a,`b,`c,… и доверительные интервалы D a, Db, Dc,... по правилам, изложенным выше для прямых измерений. При этом значения погрешностей D a, Db, Dc,... определяют с помощью коэффи­циентов Стьюдента при одинаковом значении надежности у.

2. Находят ширину доверительного интервала D Z для результата косвенных измерений:

где (дf/да)₀, (дf/дb)₀ и т.д. означают, что частные производные по соответствующему аргументу a, b, с,... вычисляют при средних зна­чениях аргументов: а = ` а, b == `b, с = `с,....

3. Находят среднее значение Z как значение функции/при средних значениях аргументов: `Z=f(`a,`b,`c,...).

4. Окончательный результат записывают в виде Z=`Z < Z. 2-й способ. Если косвенные измерения проводятся в невос­производимых условиях, то для каждого отдельною (i-го) цикла из n измерений аргументов a_i, b_i, с_i,.., вычисляют значения

Z_i согласно виду функции f, и по значениям Z_i вычисляют его

среднее значение `Z. Затем определяют границы доверительного интервала D Z, обрабатывая значения результатов Z_i так же, как

это делается для прямых измерений (при числе свободы m = n-l),

18. Объяснение случайного характера оценки показателей качества деталей

При изготовлении партии деталей все они не могут быть получены однородными (одинаковыми) по качественным при­знакам. Даже при неизменных условиях обработки происходит разброс (или, как говорят, "рассеяние") размеров деталей, причем это рассеяние может происходить либо в пределах поля (вели­чины и расположения) допуска, и тогда все детали будут год­ными, либо в более широких пределах, и тогда часть деталей будет браком. То же самое относится и к другим качественным параметрам деталей: шероховатости поверхности, биению, соосности или параллельности поверхностей и т.д. Размер детали является результатом совместного и непрерывного действия ряда случайных и систематически действующих факторов, каждый из которых стремится изменить размер в ту или иную сторону. По этим причинам результат измерения конкретной детали является случайной величиной.

При измерении партии деталей или при повторных измере­ниях одной и той же детали появление того или иного кон­кретного числового значения случайной величины рассматрива­ется как случайное событие, т.е. событие, результат которого заранее может быть предсказан только с какой-то долей досто­верности (как говорят, "с некоторой вероятностью"). Поэтому обработку результатов измерений проводят на основе теории ве­роятности и математической статистики.

19. Основные (первичные) понятия теории вероятности, используемые для анализа точности обработки и контроля

Случайное событие — событие, которое при наличии сово­купности условий F может либо произойти, либо не произойти. Достоверное событие — событие, которое обязательно произой­дет при наличии условий F. Вероятностью события А называют отношение числа благоприятствующих ему случаев (исходов) т к общему числу исключающих друг друга случаев п: Р(А) == т/п. Вероятность достоверного события равна единице, невозможного

события — нулю, а случайного события — числу, заключенному между нулем и единицей (0 < Р(А) < 1). Таким образом, для про­извольного случайного события справедливо неравенство 0£Р(А)£1. Случайная величина Х — величина, наблюдаемое значение которой зависит от случайных причин и поэтому на­перед неизвестно. Случайные величины могут быть дискретными (например, число бракованных деталей в партии и др.) или не­прерывными (например, отклонение размера детали от номинала, высота микропрофиля в данной точке и др.). Полный набор всех возможных значений случайной величины Х называется ге неральной совокупностью.

Закон распределения случайной величины Х — всякое соот­ношение, устанавливающее связь между возможными значения­ми x_i случайиой величины Х и соответствующими им вероят­ностями p_i. Его можно задать таблично, аналитически (форму­лами) или графически. В наиболее обобщенной форме закон распределения описывается с помощью интегральной функции распределения или дифференциальной функцией распределения.

 

20. Интегральная функция распределения

Функция распределе­ния F(x) — это функция, определяющая вероятность того, что случайная величина Х примет значение меньше данного значе­ния x: F(x)=P(X<x). Из определения следует, что 0£ F(x) £ 1, причем F(-оo)=0 и F(+oo)=l. Вероятность того, что значение случайной функции попадет в интервал (a, b), равна разности значений интегральной функции на концах интервала:

21. Дифференциальная функция распределения

Плотность веро­ятности f(x) — это первая производная от функции распреде­ления. График функции f(x) называют кривой распределения. Вероятность попадания Х в заданный интервал (a, b) равна

Геометрически эта вероятность равна площади криволиней­ной трапеции, ограниченной осью абсцисс, прямыми х = а и х == b и кривой распределения (рис. 1, а). Площадь под всей кривой равна единице.

 

22. Характеристики случайных величин.

Числовые ха­рактеристики случайных величин делят на 3 группы: а) харак­теристики положения случайной величины на числовой оси (ма­тематическое ожидание, мода, медиана); б) характеристики рас-

сеяния вокруг некоторого центра группирования (дисперсия, среднее квадратическое отклонение); в) моменты (начальные и центральные).

Математическое ожидание М(Х) (или т_x) — это среднее значение случайной величины Х из генеральной совокупности:

Рис. 1. Показатели несимметричности кривых распределения:

а — положительная ассиметрия; б — отрицательная ассиметрия

Мода Мо (X) — это значение Х_i с наибольшей вероятностью (или плотностью вероятности). Медиана Me (X) — значение Хёнёi, при котором площадь под кривой распределения делится пополам. В общем случае значения М(Х), Мо(Х), Me (X) могут не совпадать (рис. 1, б).

Дисперсия D (X) случайной величины X— это математическое ожидание квадрата отклонения случайной величины от ее ма­тематического ожидания:

Среднее квадратическое отклонение s_x — это корень квадратный из дисперсии (является моментом второго порядка).

Моменты больших порядков используют для описания формы кривой распределения. Так, третий центральный момент (^3)

применяют для оценки ассиметрии (скошенности) кривой распределения относительно математического ожидания, вычисляя с его помощью коэффициент ассиметрии А:

Если мода Мо(Х) находится слева от среднего значения т_x, то ассиметрия положительна. Если мода расположена справа от среднего значения,, то ассиметрия отрицательна (см. рис. 1). Четвертый центральный момент (m₄) характеризует "остроту" вершины кривой распределения. Для этого вычисляют коэффициент эксцесса Е:

Эксцесс положителен для островершинных кривых распре­деления и отрицателен для плосковершинных. Для закона Гаусса Е=0.

23. Использование законов распределения случайных величин

Законы распределения широко используются для управления параметрами ТП с тем, чтобы обеспечить показатели качества деталей в заданных пределах. С их помощью определяют запас надежности TII для обеспечения обработки деталей без брака. Они помогают рассчитать процент вероятного брака, определить количество деталей, требующих дополнительной обработки, позволяют сопоставить точность обработки на различном оборудовании, оснастке, инструменте, проводить настройку станков, комплектовать детали для сборки. По виду кривых распределения можно судить о наличии сильнодействующих факторов в процессе и наметить пути управления ТП. С их помощью организуют процесс технических измерений, определяют количество деталей из партии, подлежащих измерениям (как говорят, "объем выборки") и периодичность измерений, оценивают "риск производителя" (когда ошибочно бракуют годные изделия) и "риск потребителя" (когда ошибочно принимают бракованные детали как годные), определяют погрешности измерений.

Вид кривой распределения (закон распределения) случайной величины зависит от природы и условий образования этой ве­личины. На практике часто встречаются следующие законы (рис. 2): а) закон Гаусса (нормального распределения) — описывает, в частности, рассеяние размеров в партии деталей средней точности (12...9 квалитетов), а также погрешность результатов измерений; б) закон равнобедренного треугольника (закон Симпсона) — при обработке с точностью 6...8 квалитетов; в) закон равной вероятности — при обработке высокоточных деталей (4...5 квалитет); г) закон эксцентриситета (закон Релея) — при обеспечении допусков расположения (биения, параллельности, перпендикулярности и др.); д) показательный закон — при оценке надежности работы изделий; е) различные комбинации этих законов и др.