Определение и исключение грубых погрешностей измерений.

Установлены критерии для выявления промахов. Если априорно известна точность измерений через величину СКО (σ), то при нормальном распределении экспериментальных данных предельно допустимые отклонения от среднего значения, составляют не более чем:

2/3 σ с вероятностью не менее Р=0,5;

σ с вероятностью не менее Р=0,68;

2 σ с вероятностью не менее Р=0,95;

2,6 σ с вероятностью не менее Р=0,99;

3 σ с вероятностью не менее Р=0,997.

Последнее правило является «правилом трёх сигм»: если при многократных измерениях одного и того же постоянного размера сомнительное значение результата измерений отличается от среднего значения больше, чем на 3σ, то его следует отбросить.

В большинстве случаев СКО не известно. Тогда промахи определяются по критериям:

· Романовского, при числе измерений n≤20. 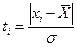, где x_i –проверяемое экспериментальное данное. Значение t_i сравнивается с табличным t_T. Если t_i_≥ t_T_, то проверяемое значение считается промахом.

· Шарлье, при большом числе измерений 20< n <100. Промахом считаются результаты, для которых выполняется неравенство: 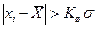, где К_ш значения критерия Шарлье (табличные).

· Диксона, при небольшом числе экспериментальных данных: 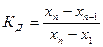, где x_n – проверяемое значение, х₁ первое в ряду. Значение является промахом, если К_Д>z_q, z_q – табличное значение, для числа измерение n и заданного уровня значимости q.

· Шовине, при n<10. Промахом считаются результаты, для которых выполняется неравенство: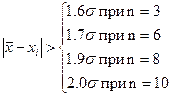

Задача. Проведены прямые многократные измерения кислотности раствора, представленные в таблице.

Результаты измерений кислотности раствора

Результаты измерений, рН	0,6	0,75	0,82	0,91	0,95	1,2
Число измерений, m_i

Проверьте ряд на отсутствие промахов.

Решение.

Воспользуемся критерием Шарлье. Рассчитаем среднее арифметическое значение и СКО:

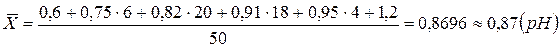
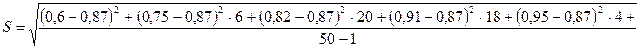
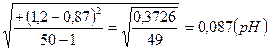
К_ш определяем по приложению для n=50 К_ш=2,32.

Проверяем значение 0,6 рН:

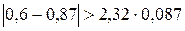
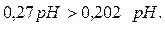
Значение 0,6 рН является промахом.

Для значения 1,2 рН: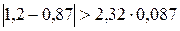

Значение 1,2 рНявляется промахом.

После исключения значений 0,6 и 1,2 рН пересчитываем среднее арифметическое значение и СКО:

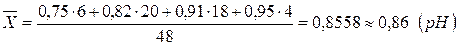
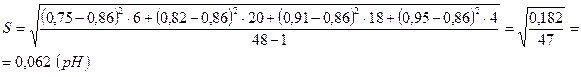
Проверяем значение 0,75 рН:

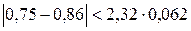
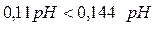
Значение 0,75 рНне является промахом.

Косвенные измерения.

косвенные измерения предполагают наличие функциональной связи Y=f(x₁, x₂, …x_n), где х₁, х₂, …х_n – подлежащие прямым измерениям аргументы функции Y.

Этапы:

1. Среднее арифметическое значение каждой измеряемой величины (аргумента):

2. ,

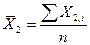
3. СКО среднего арифметического каждого аргумента:

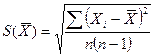
Определяем среднеарифметическое функции (измеряемой величины):

5. СКО среднего арифметического измеряемой величины:

находят границы доверительного интервала
окончательный результат записывают в виде 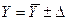при вероятности Р.

Относительная погрешность представляется в виде .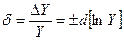

В таблице представлены выражения для упрощенного расчета относительной погрешности δ физической величины х, измеряемой косвенно и зависящей от величин a и b, имеющих абсолютные погрешности Δ a и Δ b.

	Х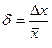
	C(a+ b)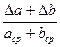
	С(a- b)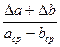
	С a b С a/ b
	C a^k bⁿ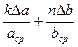

Задача: Произведены многократные измерения мощности и силы тока, на основании которых рассчитывается результат измерений сопротивления по формуле R=P/I². Экспериментальные данные:

Р, Вт – 10,2; 10,8; 9,1; 10,0; 10,4; 10,9; 11,0; 10,7; 10,3;10,5.

I, А – 32,8; 33,0 32,2; 31,6; 31,9; 32,5; 33,4; 32,6; 32,3; 32,0.

Доверительная вероятность Р=0,95.

Вычислить результат косвенных измерений в форме доверительного интервала;

Решение.

1. Среднее арифметическое значение измеряемой величины:

=10,39 Вт

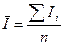=32,43 А

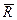=P/I²=10,39/32,43²=0,01 Ом

2. СКО среднего арифметического каждого аргумента:

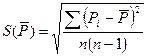
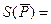0,526213≈0,53 Вт

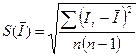
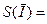0,512 А

3. СКО среднего арифметического измеряемой величины:

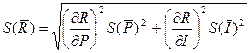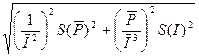
0,0016 Ом

4. Границы доверительного интервала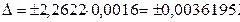

t_P= 2.2622, при Р=0,95 и n=10

5. Округляем значение погрешности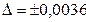

6. окончательный результат записывают в виде 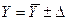при вероятности Р.

Ответ:

Результата косвенных измерений сопротивления электоцепи

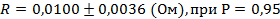
ПРИЛОЖЕНИЯ

Значения критерия Шарлье

п
К_ш	1,3	1,65	1,96	2,13	2,24	2,32	2,58

Критические значения коэффициента Стьюдента для доверительной вероятности P и числа степеней свободы n-1:

n-1	P
0.80	0.90	0.95	0.98	0.99	0.995	0.998	0.999
	3.0770	6.3130	12.706	31.820	63.656	127.656	318.306	636.62
	1.8850	2.9200	4.3020	6.964	9.924	14.089	22.327	31.599
	1.6377	2.3534	3.182	4.540	5.840	7.458	10.214	12.924
	1.5332	2.1318	2.776	3.746	4.604	5.597	7.173	8.610
	1.4759	2.015	2.570	3.649	4.0321	4.773	5.893	6.863
	1.4390	1.943	2.4460	3.1420	3.7070	4.316	5.2070	5.958
	1.4149	1.8946	2.3646	2.998	3.4995	4.2293	4.785	5.4079
	1.3968	1.8596	2.3060	2.8965	3.3554	3.832	4.5008	5.0413
	1.3830	1.8331	2.2622	2.8214	3.2498	3.6897	4.2968	4.780
	1.3720	1.8125	2.2281	2.7638	3.1693	3.5814	4.1437	4.5869
	1.363	1.795	2.201	2.718	3.105	3.496	4.024	4.437
	1.3562	1.7823	2.1788	2.6810	3.0845	3.4284	3.929	4.178
	1.3502	1.7709	2.1604	2.6503	3.1123	3.3725	3.852	4.220
	1.3450	1.7613	2.1448	2.6245	2.976	3.3257	3.787	4.140
	1.3406	1.7530	2.1314	2.6025	2.9467	3.2860	3.732	4.072
	1.3360	1.7450	2.1190	2.5830	2.9200	3.2520	3.6860	4.0150
	1.3334	1.7396	2.1098	2.5668	2.8982	3.2224	3.6458	3.965
	1.3304	1.7341	2.1009	2.5514	2.8784	3.1966	3.6105	3.9216
	1.3277	1.7291	2.0930	2.5395	2.8609	3.1737	3.5794	3.8834
	1.3253	1.7247	2.086	2.5280	2.8453	3.1534	3.5518	3.8495
	1.3230	1.7200	2.079	2.5170	2.8310	3.1350	3.5270	3.8190
	1.3212	1.7117	2.0739	2.5083	2.8188	3.1188	3.5050	3.7921
	1.3195	1.7139	2.0687	2.4999	2.8073	3.1040	3.4850	3.7676
	1.3178	1.7109	2.0639	2.4922	2.7969	3.0905	3.4668	3.7454
	1.3163	1.7081	2.0595	2.4851	2.7874	3.0782	3.4502	3.7251
	1.315	1.705	2.059	2.478	2.778	3.0660	3.4360	3.7060
	1.3137	1.7033	2.0518	2.4727	2.7707	3.0565	3.4210	3.6896
	1.3125	1.7011	2.0484	2.4671	2.7633	3.0469	3.4082	3.6739
	1.3114	1.6991	2.0452	2.4620	2.7564	3.0360	3.3962	3.8494
	1.3104	1.6973	2.0423	2.4573	2.7500	3.0298	3.3852	3.6460
	1.3080	1.6930	2.0360	2.4480	2.7380	3.0140	3.3650	3.6210
	1.3070	1.6909	2.0322	2.4411	2.7284	3.9520	3.3479	3.6007
	1.3050	1.6883	2.0281	2.4345	2.7195	9.490	3.3326	3.5821
	1.3042	1.6860	2.0244	2.4286	2.7116	3.9808	3.3190	3.5657
	1.303	1.6839	2.0211	2.4233	2.7045	3.9712	3.3069	3.5510
	1.320	1.682	2.018	2.418	2.6980	2.6930	3.2960	3.5370
	1.301	1.6802	2.0154	2.4141	2.6923	3.9555	3.2861	3.5258
	1.300	1.6767	2.0129	2.4102	2.6870	3.9488	3.2771	3.5150
	1.299	1.6772	2.0106	2.4056	2.6822	3.9426	3.2689	3.5051
	1.298	1.6759	2.0086	2.4033	2.6778	3.9370	3.2614	3.4060
	1.2997	1.673	2.0040	2.3960	2.6680	2.9240	3.2560	3.4760
	1.2958	1.6706	2.0003	2.3901	2.6603	3.9146	3.2317	3.4602
	1.2947	1.6686	1.997	2.3851	2.6536	3.9060	3.2204	3.4466
	1.2938	1.6689	1.9944	2.3808	2.6479	3.8987	3.2108	3.4350
	1.2820	1.6640	1.9900	2.3730	2.6380	2.8870	3.1950	3.4160
	1.2910	1.6620	1.9867	2.3885	2.6316	2.8779	3.1833	3.4019
	1.2901	1.6602	1.9840	2.3642	2.6259	2.8707	3.1737	3.3905
	1.2888	1.6577	1.9719	2.3578	2.6174	2.8598	3.1595	3.3735
	1.2872	1.6551	1.9759	2.3515	2.6090	2.8482	3.1455	3.3566
	1.2858	1.6525	1.9719	2.3451	2.6006	2.8385	3.1315	3.3398
	1.2849	1.6510	1.9695	2.3414	2.5966	2.8222	3.1232	3.3299
	1.2844	1.6499	1.9679	2.3388	2.5923	2.8279	3.1176	3.3233
	1.2837	1.6487	1.9659	2.3357	2.5882	2.8227	3.1107	3.3150
	1.2830	1.6470	1.9640	2.3330	2.7850	2.8190	3.1060	3.3100