Размерность. Многократные измерения. Алгоритмы обработки результатов многократных измерений. Промахи.
Цель: приобретение практических навыков обработки результатов многократных прямых и косвенных измерений.
Размерность.
Формализованным отражением качественного различия физических величин является их размерность. Размерность обозначается символом dim, происходящим от слова dimension, которое в зависимости от контекста может переводиться и как размер, и как размерность.
Размерность основных физических величин обозначается соответствующими заглавными буквами:
dim l = L – размерность длины
dim m = M – размерность массы
dim t = Т – размерность времени
dim I = I – размерность силы электрического тока
dim T = Q – размерность термодинамической температуры
dim j = J – размерность силы света
dim ν = N – размерность количества вещества
При определении размерности производных величин руководствуются следующими правилами:
1. Размерности правой и левой частей уравнения не могут не совпадать, т.к. сравниваться между собой могут только одинаковые свойства. Таким образом, алгебраически могут суммироваться только величины, имеющие одинаковые размерности.
2. Алгебра размерностей мультипликативна, т.е. состоит из одного единственного действия - умножения.
2.1. Размерность произведения нескольких величин равна произведению их размерностей. Так, если зависимость между значениями величин Q, А, В, С имеет вид Q=АВС, то
dim Q = dim A×dim В×dim С.
2.2. Размерность частного при делении одной величины на другую равна отношению их размерностей, т.е. если Q=A/B, то
dim Q = dim A / dim В.
2.3. Размерность любой величины, возведенной в некоторую степень, равна ее размерности в той же степени. Так, если Q=An, то
dim Q = 
dim A = dimnA.
Например, если скорость определять по формуле V = S/t, то
dim V = dim S/dim t = L/T=LT-1.
Если сила по второму закону Ньютона F = ma, где a = V/t - ускорение тела, то
dim F = dim m dim a = ML/T2 = MLT-2.
Таким образом, всегда можно выразить размерность производной физической величины через размерности основных физических величин с помощью степенного одночлена:
dim Q = LaMbTg,
где L, М, Т, - размерности соответствующих основных физических величин; a, b, g, - показатели размерности. Каждый из показателей размерности может быть положительным или отрицательным, целым или дробным числом, нулем.
Если все показатели размерности равны нулю, то такая величина называется безразмерной. Она может быть относительной, определяемой как отношение одноименных величин (например, относительная диэлектрическая проницаемость), и логарифмической, определяемой как логарифм относительной величины (например, логарифм отношения мощностей или напряжений).
Задача. Выразите размерность электрической емкости через размерности основных физических величин SI. Определите единицу измерения электрической емкости через единицы основных физических величин.
Решение. Формула электрической емкости: 
. В системе SI за единицу заряда принимается Кулон. Кулоном называется электрический заряд, протекающий через поперечное сечение проводника за 1 с при силе тока в 1 А, т.е. 
. Напряжение U представляет собой работу, совершаемую суммарным полем кулоновских и сторонних сил при перемещении на участке цепи единичного положительного заряда: 
. Работу можно выразить через силу и путь: 
, где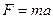 
- m – масса, 
- ускорение.
Тогда можно записать:
Размерность электрической емкости:
В системе SI единица электрической емкости может быть выражена: 
Методика обработка результатов измерений.
Многократное измерение – измерение физической величины одного и того же размера, результат которого получен из нескольких следующих друг за другом измерений, т. е. состоящее из ряда однократных измерений (выполненных не менее 4 раз).
За результат многократного измерения обычно принимают среднее арифметическое значение из результатов однократных измерений, входящих в ряд.
Эти измерения повторяются оператором в одинаковых условиях, использующим одни и те же средства измерений. Такие измерения характерны при выполнении метрологических работ, а также находят широкое применение в научных исследованиях. По результатам многократных измерений проводится анализ, главной особенностью которого является получение и использование большого объема измерительной информации.
Прежде чем приступить к обобщению результатов измерений, определяют, нет ли в полученных результатах грубых погрешностей.
Применение многократных измерений позволяет повысить точность измерения до определенного предела, но недостаток полученной информации не позволяет получить точное значение поправок, значений составляющих погрешностей и т.п. В связи с этим устанавливают необходимое число измерений, которое позволяет получить результат измерений, в котором случайная погрешность пренебрежимо мала по сравнению с неисключенной систематической погрешностью. Число измерений находят по формуле n = 64(s/q) где s – среднее квадратическое отклонение ряда измерений, q – неисключенная систематическая погрешность.
