Апроксимацiя функцiй однiєї змiнної узагальненим полiномом
У попередньому пунктi розглянуто найпростiший випадок, коли апроксимуюча функцiя є полiномом степеня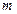 
. Узагальнимо його, припустивши, що апроксимуюча функцiя має вигляд
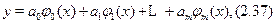
тобто є лiнiйною комбiнацiєю функцiй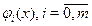 
, якi належать деякiй системi лiнiйно незалежних функцiй. Вираз (2.37) називається узагальненим полiномом по системi функцiй .
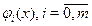Метод найменших квадратiв в цьому випадку полягає у знаходженнi серед узагальнених полiномiв такого, для якого функцiя
приймає мiнiмальне значення. Аналогiчно попередньому приходимо до нормальної системи рiвнянь, яка має вигляд:
Якщо ввести позначення
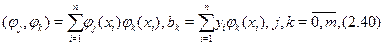
то систему (2.39) можна записати у виглядi матричного рiвняння
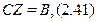
де
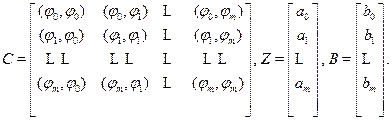
Визначник системи (2.39) є визначником Грама функцiй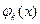 
. Оскiльки цi функцiї, за припущенням, лiнiйно незалежнi, то вiн вiдмiнний вiд нуля. Отже, розв'язок системи iснує i єдиний.
Якщо при побудовi апроксимуючої функцiї використовується система лiнiйно незалежних функцiй, яка є ортогональною, тобто
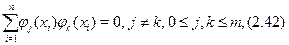
то система (2.39) спрощується i матриця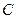 
стає дiагональною. Параметри наближення обчислюються за формулою
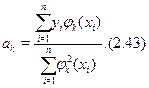
З погляду на це зручно застосовувати ортогональну систему лiнiйно незалежних функцiй.
Для перевiрки вiдповiдностi побудованої емпiричної формули експериментальним даним, по-перше, обчислюють значення апроксимуючої функцiї при табличних значеннях аргумента та порiвнюють цi значення з експериментальними (табличними) значеннями функцiї; по-друге, обчислюють середньоквадратичну похибку акпроксимацiї за формулою
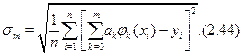
Якщо 
, де 
--- абсолютна похибка експериментальних даних, тобто, якщо математична похибка апроксимацiї значно бiльша фiзичної похибки вихiдних даних, то кiлькiсть коефiцiєнтiв 
недостатня для опису 
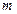i треба збiльшити . Якщо 
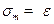, то старшi коефiцiєнти апроксимацiї фiзично не є вiрогiдними i треба зменшити 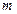. Якщо 
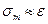, то кiлькiсть коефiцiєнтiв оптимальна.
Апроксимацiя функцiй однiєї змiнної елементарними функцiями, вiдмiнними вiд полiнома
Якщо емпiрична формула нелiнiйна вiдносно параметрiв, то її лінеаризують, тобто шляхом деяких перетворень вихідних змінних подають у вигляді лінійної функції.
Нехай, наприклад, апроксимуюча функцiя має вигляд
Припускаючи, що у вихiднiй таблицi даних значення аргумента i значення функцiї додатнi, застосуємо попереднє логарифмування (при умовi 
):
Позначимо
тодi рiвнiсть (2.46) набуває вигляду
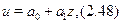
тобто в системi координат 
отримали лiнiйну залежнiсть.
На практиці, для знаходження апроксимуючої функцiї у виглядi (2.45) (в умовах зроблених припущень) необхiдно: 1) по заданiй таблицi скласти нову таблицю, прологарифмувавши значення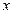 
та 
у вихiднiй таблицi; 2) за даними нової таблицi методом найменших квадратiв знайти параметри 
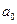i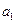 
апроксимуючої функцiї (2.48); 3) використовуючи формули (2.47), знайти значення параметрiв 
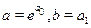i пiдставити їх у вираз (2.45). Це i буде шукана емпiрична формула.
Описаний алгоритм можна застосувати також i в деяких iнших випадках, коли емпiрична формула не є полiномом, але шляхом вiдповiдної замiни змiнних зводиться до нього. Замiни змiнних, якi зводять степеневу, показникову, гiперболiчну, логарифмiчну залежностi до лiнiйної, наведенi у таблицi 2.6.
Таблиця 2.6
Приклад 2.6. Методом найменших квадратів побудувати функцію, апроксимуючу залежність, яка задана таблицею,
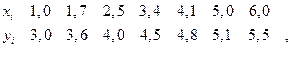
у виглядi елементарної функцiї 
.
Розв'язування. Згiдно з таблицею 2.6 зробимо замiну змiнних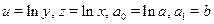 
. Тодi шукана залежнiсть набуває вигляду
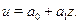
Параметри 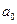i 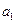знаходяться так само, як i в прикладi 2.5, але за основу береться нова таблиця значень змiнних 
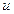i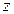 
.
Система лiнiйних алгебраїчних рiвнянь вiдносно невiдомих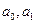 
(нормальна система) у цьому випадку має вигляд
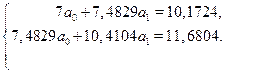
Розв'язавши її, отримуємо 
.
Звiдси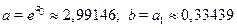 
.
Шукана емпiрична формула має вигляд
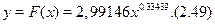
Обчислимо середньоквадратичну похибку апроксимацiї даної залежностi функцiєю (2.49)
Для цього складемо нову таблицю
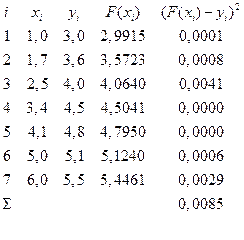
Таким чином, із останьої колонки таблиці отримуємо
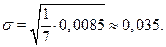
Порівнюючи середньоквадратичні похибки 
i 
(з прикладу 2.6) можна зробити висновок, що ця функцiя краще наближує дану експериментальну залежнiсть, нiж лiнiйна функцiя (2.36).
