Решение:
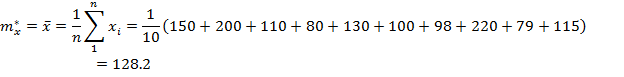
= 48.325
При n=10 и α=0.95 t=2.228
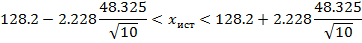
Ответ:
Задача 20.
Дано: Оценить увеличение энтропии при производстве бинарной системной информации емкостью в одну терабиту.
Решение:
второй закон термодинамики, информационная энтропия по определению
, здесь 
- плотность функции распределения величины x, x – измеряемая величина, а интегрирование проводится по всему пространству, в дискретном случае вводят 
, где 
- вероятность того, что система пребывает в i-ом состоянии. Тогда так как возникновение какого-либо количества бит информации связано с тепловым фоном (т.е. с температурой, и с изменением тепловой энергии 
), то получаем, что производство информации N вызывает изменение, как энтропии, так и информационной энтропии: 
. Поэтому для решения задачи остается установить между ними функциональную и количественную связь.
В случае дискретной величины X, последняя будет иметь n-равновесных значений. Из равной вероятности реализации каждого из них (она равна 
), получаем следуя определению для информационной энтропии выражение 
, где
-число возможных состояний системы. Между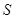 
и 
установлена связь 
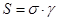, где
Таким образом, получаем, что для бинарной системы производство информации в один бит увеличивает энтропию в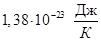 
(т.е.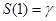 
).
Тогда, создание информации в 1 бит вызывает 
. Действительно, энтропия обращается в ноль, если состояние системы достоверно (p=1), т.е. 
:
т.е. до измерений энтропия была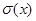 
, после стала 0, значит 
; итак, количество получаемой информации при выяснении состояния системы равно изменению её информационной энтропии; тогда, для ситуации с равновероятными значениями событий, получаем: 
.
Значит, создание информации в 1 бит в бинарной системе (n=2) вызывает изменение энтропии 
. Значит, для записи N бит информации необходимо изменить энтропию на следующую величину: 
(Двойка появилась из-за того, что при создании информации в 1 бит приходится выбирать в бинарном случае из двух состояний). А если изменилась энтропия, значит необходимо рассеять тепло (по второму закону термодинамики).
Так как 
и , то 
. Итак, создание информации в N бит изменяет энтропию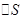 
(это фундаментальное свойство любой системы), а последнее по второму закону Ньютона требует рассеяния тепла. Далее вступают в силу характеристики материалов и условий эксперимента – в частности насколько эффективно мы это тепло отводим.
Так как мы имеем дело с дискретным случаем, у нас есть два состояний – 0 и 1, то мы имеем, что энтропия системы , а 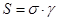. Тогда, создание информации в 1 бит вызывает . и в итоге имеем 
Ответ:
Задача 21.
