1. Функция  , определенная на множестве
, определенная на множестве  , называется четной, если
, называется четной, если 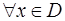 выполняются условия:
выполняются условия: 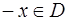 и
и  ; нечетной, если
; нечетной, если 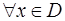 выполняются условия:
выполняются условия: 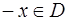 и
и  .
.
График четной функции симметричен относительно оси 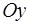 , а нечетной — относительно начала координат.
, а нечетной — относительно начала координат.
Например, 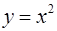 ,
,  ,
,  — четные функции; а
— четные функции; а  ,
, 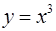 — нечетные функции;
— нечетные функции;  ,
,  — функции общего вида, т. е. не четные и не нечетные.
— функции общего вида, т. е. не четные и не нечетные.
 2. Пусть функция
2. Пусть функция  определена на множестве
определена на множестве  и пусть
и пусть 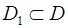 . Если для любых значений
. Если для любых значений  аргументов из неравенства
аргументов из неравенства 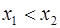 вытекает неравенство
вытекает неравенство  , то функция называется возрастающей
, то функция называется возрастающей
на множестве 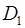 ;
;  то функция называется неубывающей на множестве
то функция называется неубывающей на множестве 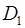 ;
; 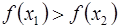 , то функция называется убывающей на множестве
, то функция называется убывающей на множестве 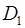 ,
,  , то функция называется невозрастающей на множестве
, то функция называется невозрастающей на множестве 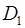 .
.
Например, функция, заданная графиком (рис. 2), убывает на интервале  , не убывает на интервале
, не убывает на интервале  , возрастает на интервале
, возрастает на интервале  .
.
Возрастающие, невозрастающие, убывающие и неубывающие функции на множестве 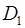 называются монотонными на этом множестве, а возрастающие и убывающие — строго монотонными. Интервалы, в которых функция монотонна, называются интервалами монотонности. На рисунке (выше) функция строго монотонна на
называются монотонными на этом множестве, а возрастающие и убывающие — строго монотонными. Интервалы, в которых функция монотонна, называются интервалами монотонности. На рисунке (выше) функция строго монотонна на  и
и  ; монотонна на
; монотонна на  .
.
3. Функцию  , определенную на множестве
, определенную на множестве  , называют ограниченной на этом множестве, если существует такое число
, называют ограниченной на этом множестве, если существует такое число  , что для всех
, что для всех  выполняется неравенство
выполняется неравенство  . Отсюда следует, что график ограниченной функции лежит между прямыми
. Отсюда следует, что график ограниченной функции лежит между прямыми  и
и  (рис. 3).
(рис. 3).


4. Функция  , определенная на множестве
, определенная на множестве  , называется периодической на этом множестве, если существует такое число
, называется периодической на этом множестве, если существует такое число  , что при каждом
, что при каждом  значение
значение  и
и  . При этом число
. При этом число  называется периодом функции. Если
называется периодом функции. Если  — период функции, то ее периодами будут также числа
— период функции, то ее периодами будут также числа  , где
, где  . Так, для
. Так, для  периодами будут числа
периодами будут числа  ;
; 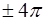 ;
;  ,.... Основной период (наименьший положительный) — это период
,.... Основной период (наименьший положительный) — это период  . Вообще обычно за основной период берут наименьшее положительное число
. Вообще обычно за основной период берут наименьшее положительное число  , удовлетворяющее равенству
, удовлетворяющее равенству  .
.
Обратная функция.
Пусть задана функция  с областью определения
с областью определения  и множеством значений
и множеством значений  . Если каждому значению
. Если каждому значению 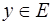 соответствует единственное значение
соответствует единственное значение  , то определена функция
, то определена функция  с областью определения
с областью определения  и множеством значений
и множеством значений  . Такая функция
. Такая функция  называется обратной к функции
называется обратной к функции  и записывается в следующем виде:
и записывается в следующем виде: 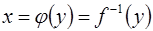 . Про функции
. Про функции  и
и  говорят, что они являются взаимно обратными. Чтобы найти функцию
говорят, что они являются взаимно обратными. Чтобы найти функцию  , обратную к функции
, обратную к функции  , достаточно решить уравнение
, достаточно решить уравнение  относительно
относительно  (если это возможно).
(если это возможно).
Примеры.
- Для функции
 обратной функцией является функция
обратной функцией является функция  .
.
2. Для функции 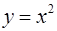 ,
,  , обратной функцией является
, обратной функцией является  ; заметим, что для функции
; заметим, что для функции 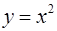 , заданной на отрезке
, заданной на отрезке  , обратной не существует, т. к. одному значению
, обратной не существует, т. к. одному значению  соответствует два значения
соответствует два значения  (так, если
(так, если  , то
, то 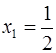 ,
,  ).
).
Из определения обратной функции вытекает, что функция  имеет обратную тогда и только тогда, когда функция
имеет обратную тогда и только тогда, когда функция  задает взаимно однозначное соответствие между множествами
задает взаимно однозначное соответствие между множествами  и
и  . Отсюда следует, что любая строго монотонная функция имеет обратную. При этом если функция возрастает (убывает), то обратная функция также возрастает (убывает).
. Отсюда следует, что любая строго монотонная функция имеет обратную. При этом если функция возрастает (убывает), то обратная функция также возрастает (убывает).
Сложная функция
Пусть функция  определена на множестве
определена на множестве  , а функция
, а функция  на множестве
на множестве 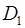 , причем для
, причем для  соответствующее значение
соответствующее значение  . Тогда на множестве
. Тогда на множестве 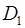 определена функция
определена функция 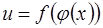 , которая называется сложной функцией от
, которая называется сложной функцией от  (или суперпозицией заданных функций, или функцией от функции).
(или суперпозицией заданных функций, или функцией от функции).
Переменную  называют промежуточным аргументом сложной функции.
называют промежуточным аргументом сложной функции.
Например, функция  есть суперпозиция двух функций
есть суперпозиция двух функций  и
и  . Сложная функция может иметь несколько промежуточных аргументов.
. Сложная функция может иметь несколько промежуточных аргументов.




