Основные элементарные функции и их графики.

ВВЕДЕНИЕ В АНАЛИЗ

Л е к ц и я 7

ФУНКЦИИ И ИХ ХАРАКТЕРИСТИКИ.

ПЛАН

Числовые функции. График функции. Способы задания функций.

Основные характеристики функции.

Обратная функция.

Сложная функция.

Основные элементарные функции и их графики.

1. Пусть даны 2 непустых множества и .

Определение. Если ставится в соответствие по правилу единственный элемент , то говорят, что на множестве задана функция и пишут: .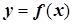

называется областью определения функции; - областью (множеством) значений.

Функции обозначаются латинскими буквами: , , , , ,

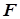Пусть задана функция .

Если элементами множеств 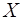и являются действительные числа (т. е. и 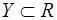), то функцию называют числовой функцией. В дальнейшем будем изучать (как правило) числовые функции, для крат­кости будем именовать их просто функциями и записывать .

Переменная называется при этом аргументом или независимой переменной, а — функцией или зависимой переменной (от ). Относительно самих величин и говорят, что они находятся в функциональной зависимости. Иногда функциональную зависимость от пишут в виде , не вводя новой буквы () для обозначения зависимости.

Частное значение функции при 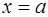записывают так: . На­пример, если , то , .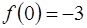

Графиком функции называется множество всех точек плоскости 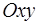, для каждой из которых является значением аргумента, а — соответствующим значением функции.

Например, графиком функции является верхняя полуокружность радиуса с центром в (рис. 1).

Чтобы задать функцию , необходимо указать правило, позволяющее, зная , находить со­ответствующее значение .

Наиболее часто встречаются три способа задания функции: аналитический, табличный, графический.

 

 

Аналитический способ: функция задается в виде одной или несколь­ких формул или уравнений.

Например:

1) ;

2)

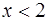при , при ,

3) .

 

Если область определения функции не указана, то предполагается, что она совпадает с множеством всех значений аргумента, при которых соответствующая формула имеет смысл. Так, областью определения функции является отрезок .

Аналитический способ задания функции является наиболее совершенным, так как к нему приложены методы математического анализа, позво­ляющие полностью исследовать функцию .

Графический способ: задается график функции.

Табличный способ: функция задается таблицей ряда значений аргумента и соответствующих значений функции. Например, известные табли­цы значений тригонометрических функций, логарифмические таблицы.

На практике часто приходится пользоваться таблицами значений функций, полученных опытным путем или в результате наблюдений.