ИКТИБ ИТА ЮФУ
КУРС ЛЕКЦИЙ ПО МАТЕМАТИКЕ
Лекция 16 Вычисление производных и дифференциалов функции
План лекции
Доказательство правил вычисления производных и формул таблицы производных. Вычисление производных и дифференциалов различным образом заданных функций. Вычисление производных и дифференциалов функций высших порядков.
Вычисление производной функции
Производная функции играет важную роль в различных приложениях математики, поэтому необходимо знать – в каких случаях можно вычислить производную и как это сделать.
Мы познакомились с основными элементарными и знаем, что все элементарные функции получаются из основных элементарных функций с помощью операций сложения, вычитания, умножения, деления и взятия функции от функции (суперпозиции функций). Мы научимся вычислять производную любой элементарной функции. Для этого будет обоснована таблица производных основных элементарных функций и выведены правила вычисления производной суммы, разности, произведения, частного и суперпозиции функций.
С понятием производной мы познакомились на прошлой лекции и следовали при этом истории появления понятий дифференциала и производной. Историческое развитие не всегда является прямолинейным. Поэтому в современном изложении этого материала вначале, как правило, появляется понятие производной, а только затем понятие дифференциала. И происходит это примерно следующим образом.
Производной функции  называется предел отношения приращения функции к приращению аргумента, если этот предел существует. Это можно записать в виде
называется предел отношения приращения функции к приращению аргумента, если этот предел существует. Это можно записать в виде 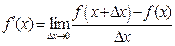 , имея в виду, что величина
, имея в виду, что величина  является приращением аргумента,
является приращением аргумента,  - приращением функции. Если этот предел не существует, то мы говорим, что функция не имеет производную в этой точке.
- приращением функции. Если этот предел не существует, то мы говорим, что функция не имеет производную в этой точке.
Затем вводится понятие дифференциала функции, как главной части  приращения функции, если это приращение представляется в виде
приращения функции, если это приращение представляется в виде  , где
, где 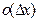 - функция, обладающая свойством
- функция, обладающая свойством  . При этом также, как мы и делали, доказывается теорема о том, что функция дифференцируема тогда и только тогда, когда существует производная этой функции. При этом
. При этом также, как мы и делали, доказывается теорема о том, что функция дифференцируема тогда и только тогда, когда существует производная этой функции. При этом  и для дифференциала функции справедлива формула
и для дифференциала функции справедлива формула  . Заметим, что из дифференцируемости функции следует ее непрерывность. В частности, отсюда следует, что функция, имеющая производную в точке, непрерывна в этой точке.
. Заметим, что из дифференцируемости функции следует ее непрерывность. В частности, отсюда следует, что функция, имеющая производную в точке, непрерывна в этой точке.
Правила вычисления производной функции
Теорема 1. Пусть существуют производные функций  и
и  Тогда справедливы формулы:
Тогда справедливы формулы:  ,
,  ,
,  ,
,  .
.
Доказательство. Так как существуют производные функций  и
и  , то
, то 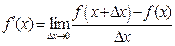 и
и  . Докажем первую из формул. Рассмотрим
. Докажем первую из формул. Рассмотрим  и после простой группировки слагаемых получим
и после простой группировки слагаемых получим  . Вторая формула доказывается совершенно аналогично. Далее рассмотрим с учетом определения производной
. Вторая формула доказывается совершенно аналогично. Далее рассмотрим с учетом определения производной 

 оказывается справедливой третья формула (с учетом непрерывности этих функций). Аналогично доказывается формула № 4, после чего теорема будет доказана.
оказывается справедливой третья формула (с учетом непрерывности этих функций). Аналогично доказывается формула № 4, после чего теорема будет доказана.
Теорема 2. Пусть существуют производные функций  и
и  . Тогда существует производная функции
. Тогда существует производная функции  и справедлива формула
и справедлива формула  .
.
Доказательство. Сформулируем идею доказательства. Для функции  рассмотрим отношение приращения функции к приращению аргумента функции
рассмотрим отношение приращения функции к приращению аргумента функции 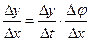 . С учетом существования (по условию теоремы) производных соответствующих функций при переходе к пределу в этом равенстве (все приращения в силу непрерывности одновременно стремятся к 0) мы приходим к формуле
. С учетом существования (по условию теоремы) производных соответствующих функций при переходе к пределу в этом равенстве (все приращения в силу непрерывности одновременно стремятся к 0) мы приходим к формуле  . Теорема доказана.
. Теорема доказана.
Следствие. (Производная обратной функции) Пусть задана монотонная функция  . Тогда существует обратная ей функция
. Тогда существует обратная ей функция  , т. е. функция, обладающая свойством
, т. е. функция, обладающая свойством  ,
,  , и при этом справедлива формула
, и при этом справедлива формула  .
.
Доказательство. Для сложной функции  производная, с одной стороны, равна 1, а, с другой стороны, равна произведению производных
производная, с одной стороны, равна 1, а, с другой стороны, равна произведению производных 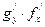 , откуда
, откуда  .
.
Таблица производных основных элементарных функций
Теорема 3. Справедливы следующие формулы для производных основных элементарных функций.
1) 
| 2) 
| 3) 
| 4) 
|
5) 
| 6) 
| 7) 
| 8) 
|
9) 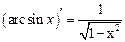
| 10) 
| 11) 
| 12) 
|
Доказательство. Формула 1) очевидна, т. к. у константы приращение функции всегда равно 0. Рассмотрим теперь формулу 4) при  , т. е. производную от натурального логарифма. Вычислим ее непосредственно:
, т. е. производную от натурального логарифма. Вычислим ее непосредственно:
 .
.
Теперь заметим, что 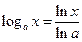 и справедлива формула
и справедлива формула  . Формула 4) доказана.
. Формула 4) доказана.
Рассмотрим функцию  , обратную к функции
, обратную к функции 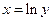 . Поэтому (производные берутся по соответствующим аргументам)
. Поэтому (производные берутся по соответствующим аргументам) 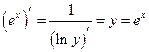 . Теперь заметим, что
. Теперь заметим, что  , поэтому, с учетом правила вычисления производной сложной функции,
, поэтому, с учетом правила вычисления производной сложной функции,  . Формула 3) доказана.
. Формула 3) доказана.
Для вычисления табличной производной 2) применим так называемое правило логарифмического дифференцирования. Суть его заключается в том, что  , и эта формула применяется, если производную от логарифма функции посчитать легче, чем от самой функции. В этом случае искомая производная вычисляется по формуле
, и эта формула применяется, если производную от логарифма функции посчитать легче, чем от самой функции. В этом случае искомая производная вычисляется по формуле 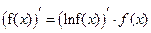 .
.
Итак, для функции  рассмотрим соотношение-следствие
рассмотрим соотношение-следствие  или
или  . Продифференцировав обе части полученного соотношения, получим
. Продифференцировав обе части полученного соотношения, получим  , откуда
, откуда  и, наконец,
и, наконец, 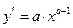 . Формула 2) доказана.
. Формула 2) доказана.
Перейдем к доказательству формул второй строки таблицы. Вычислим производную функции  после следующих преобразований:
после следующих преобразований:  . Формула 5) доказана.
. Формула 5) доказана.
Формулы 6), 7), 8) являются прямым следствием формулы 5):
 ,
,

 .
.
И, наконец, рассмотрим формулы третьей строки. Заметим, что функция  является обратной к функции
является обратной к функции 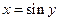 и поэтому
и поэтому  . Учитывая, что в области определения арксинуса
. Учитывая, что в области определения арксинуса 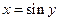 значения косинуса не могут принимать отрицательные значения, мы приходим к формуле
значения косинуса не могут принимать отрицательные значения, мы приходим к формуле  . Далее, получим
. Далее, получим  .
.
Теперь отметим, что функция  является обратной к функции
является обратной к функции  и поэтому
и поэтому  . Вспомним формулу
. Вспомним формулу  и поэтому
и поэтому  . Далее, получим
. Далее, получим  . Теорема 7 доказана.
. Теорема 7 доказана.




