Индивидуальная работа №3
Прямая и плоскость в пространстве.
Кривые второго порядка»
1. Даны четыре точки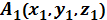 
, 
, 
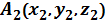и 
. Составить уравнения:
Плоскости.
Прямой.
Прямой, перпендикулярной к плоскости.
Прямой, параллельной прямой.
Плоскости, проходящей через точку перпендикулярно к прямой.
Вычислить:
Синус угла между прямой и плоскостью.
Косинус угла между координатной плоскостью и плоскостью.
Варианты:
1.1. 
, 
, 
, 
.
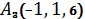1.2. 
, 
, 
, 
.
1.3. 
, 
, 
, 
.
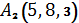1.4.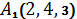 
, 
, 
, 
.
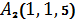1.5. 
, 
, 
, 
.
1.6. 
, 
, 
, 
.
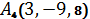1.7. 
, 
, 
, 
.
1.8. 
, 
, 
, 
.
1.9. 
, 
, 
, 
.
1.10. 
, 
, 
, 
.
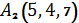1.11.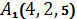 
, 
, 
, 
.
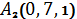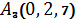1.12. 
, 
, 
, 
.
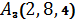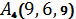1.13. 
, 
, 
, 
.
1.14. , 
, 
, 
.
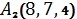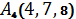1.15. 
, 
, 
, 
.
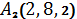1.16. 
, 
, 
, 
.
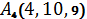1.17. 
, 
, 
, 
.
1.18. 
, 
, 
, 
.
1.19. 
, 
, 
, 
.
1.20. 
, 
, 
, 
.
1.21. 
, 
, 
, 
.
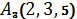1.22.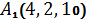 
, 
, 
, 
.
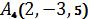1.23. 
, 
, 
, 
.
1.24. 
, 
, 
, 
.
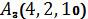1.25. 
, 
, 
, 
.
1.26.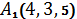 
, 
, 
, .
1.27. 
, 
, 
, 
.
1.28. 
, 
, 
, 
.
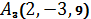1.29. 
, 
, 
, 
.
1.30. 
, 
, 
, 
.
Решить следующие задачи.
2.1. Найти величины отрезков, отсекаемых на осях координат плоскостью, проходящей через точку 
параллельно плоскости 
.
2.2. Составить уравнение плоскости, проходящей через середину отрезка 
перпендикулярно этому отрезку, если 
, 
.
2.3. Найти расстояние от точки 
до плоскости
2.4. Составить уравнение плоскости, проходящей через точку 
параллельно плоскости 
.
2.5. Составить уравнение плоскости, проходящей через ось 
и точку 
.
2.6. Составить уравнение плоскости, проходящей через точки , 
параллельно оси 
.
2.7. Составить уравнение плоскости, проходящей через точку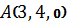 
и прямую 
.
2.8. Составить уравнение плоскости, проходящей через две параллельные прямые 
и 
.
2.9. Составить общие уравнения прямой, образованной пересечением плоскости 
с плоскостью, проходящей через ось и точку 
.
2.10. Составить уравнение плоскости в отрезках, если она проходит через точку 
и отсекает на оси отрезок 
, а на оси 
- 
.
2.11. Составить уравнение плоскости, проходящей через точку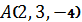 
параллельно двум векторам 
и 
.
2.12. Составить уравнение плоскости, проходящей через точки 
, 
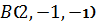перпендикулярно плоскости 
.
2.13. Составить уравнение плоскости, проходящей через начало координат перпендикулярно к двум плоскостям 
и 
.
2.14. Составить уравнение плоскости, проходящей через точки 
, 
параллельно вектору 
.
2.15. Составить уравнение плоскости, проходящей через начало координат перпендикулярно вектору 
, если 
, 
.
2.16. Найти величины отрезков, отсекаемых на осях координат плоскостью, проходящей через точку 
параллельно плоскости 
.
2.17. Составить уравнение плоскости, проходящей через точку 
перпендикулярно к отрезку , если 
, 
.
2.18. Показать, что прямая 
параллельна плоскости
, а прямая 
лежит в этой плоскости.
2.19. Составить общее уравнение плоскости, проходящей через точку 
параллельно координатной плоскости 
.
2.20. Составить уравнение плоскости, проходящей через ось и точку 
.
2.21. Составить уравнение плоскости, проходящей через точки 
, 
параллельно оси .
2.22. Составить уравнение плоскости, проходящей через точку 
и прямую 
2.23. Найти проекцию точки 
на плоскость 
.
2.24 Определить, при каком значении 
плоскости 
и 
будут перпендикулярны.
2.25. Составить уравнение плоскости, которая проходит через точку 
и отсекает на осях координат отличные от нуля отрезки одинаковой величины.
2.26. При каких значениях 
и 
прямая 
перпендикулярна к плоскости 
.
2.27. Составить уравнение плоскости, проходящей через точки 
, 
перпендикулярно к плоскости 
.
2.28. Составить уравнение плоскости, проходящей через начало координат перпендикулярно к плоскостям 
и .
2.29. Составить уравнение плоскости, проходящей через точки 
и 
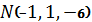параллельно вектору 
.
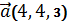2.30. Определить, при каком значении 
плоскости 
и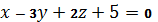 
будут перпендикулярны.
Решить следующие задачи.
3.1. Доказать параллельность прямых 
и 
3.2. Доказать, что прямая 
параллельна плоскости 
, а прямая 
лежит в этой плоскости.
3.3. Составить уравнение прямой, проходящей через точку 
и образующей с осями координат углы, соответственно равные 
, 
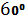и 
.
3.4. Доказать, что прямая 
перпендикулярна к прямой 
3.5. Составить параметрические уравнения медианы треугольника с вершинами 
, 
, 
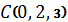, проведенной из вершины .
3.6. При каком значении прямая 
паралельна прямой 
3.7. Найти точку пересечения прямой 
и плоскости
.
3.8. Найти проекцию точки 
на плоскость 
.
3.9. При каком значении плоскости и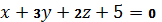 
перпендикулярны?
3.10. При каком значении плоскость 
параллельна прямой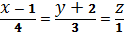 
?
3.11. При каких значениях 
и прямая 
перпендикулярна к плоскости 
?
3.12. Составить уравнение прямой, проходящей через начало координат параллельно прямой 
3.13. Проверить, лежат ли на одной прямой точк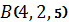и 
, 
и 
.
3.14. Составить уравнение прямой, проходящей через точку 
параллельно прямой 
3.15. Составить уравнение прямой, проходящей через точку 
перпендикулярно к прямым 
и 
.
3.16. При каких значениях и плоскость 
перпендикулярна к прямой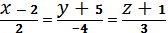 
?
3.17.Показать, что прямая 
параллельна плоскости
, а прямая лежит в этой плоскости.
3.18. Составить уравнение плоскости, проходящей через ось и точку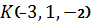 
.
3.19. Показать, что прямые 
и 
перпендикулярны.
3.20. При каком значении 
прямая 
пересекает ось ?
3.21 При каком значении прямые 
и 
параллельны?
3.22. Найти точку пересечения прямой 
и плоскости
.
3.23. Составить уравнение плоскости, проходящей через точку 
параллельно плоскости .
3.24. Составить общее уравнение прямой, образованной пересечением плоскости 
с плоскостью, проходящей через ось и точку 
.
3.25. При каких значениях и прямая 
лежит в плоскости ?
3.26. Составить уравнение плоскости, проходящей через точку 
параллельно двум векторам 
и 
.
3.27. Составить уравнение прямой, проходящей через точку 
параллельно оси .
3.28. Составить уравнение прямой, проходящей через точку 
перпендикулярно к прямой 
.
3.29. Составить каноническое уравнение прямой, проходящей через точку 
перпендикулярно к прямым 
и 
.
3.30. Найти точку, симметричную точке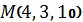 
относительно прямой
.
4. Составить канонические уравнения:
а) эллипса;
б) гиперболы;
В) параболы.
, 
- точки, лежащие на кривой, 
- фокус, 
- большая (действительная) полуось, 
- малая (мнимая) полуось, ɛ - эксцентриситет,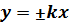 
- уравнения асимптот гиперболы, 
- директриса кривой, 
- фокусное расстояние.
Варианты:
4.1. а) 
, 
;
б) 
, 
;
в) 
.
4.2. а) 
, 
;
б) 
, 
;
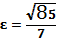в) 
.
4.3. а) 
, 
;
б) 
, 
;
в) 
.
4.4. а) 
, 
;
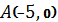б) 
, 
;
в) .
4.5. а) 
, 
;
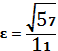б) 
, 
;
в) 
.
4.6 а) 
, 
;
б) , ;
в) 
.
4.7. а) 
, 
;
б)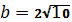 
, 
;
в) 
.
4.8. а) 
, 
;
б) 
, 
;
в)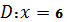 
.
4.9. а) 
, 
;
б) 
, 
;
в) 
.
4.10. а) 
, 
;
б) 
, 
;
в) 
.
4.11. а) , 
;
б) 
;
в) 
4.12. а) , 
;
б)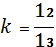 
, ;
в) 
.
4.13. а)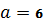 
, 
;
б) 
, 
;
в)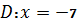 
.
4.14. а) 
, 
;
б) 
, 
;
в) 
.
4.15. а) 
, 
;
б) 
, 
;
в) 
.
4.16. а)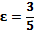 
, 
;
б) 
, 
;
в) 
.
4.17. а) , 
;
б) 
, 
;
в) 
.
4.18. а) 
, 
;
б) 
, 
;
в) 
.
4.19. а) 
, ;
б) 
, 
;
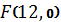в) 
.
4.20. а) , ;
б) , 
;
в) 
.
4.21. а) 
, 
;
б) 
, 
;
в) 
.
4.22. а)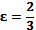 
, 
;
б) 
, 
;
в) .
4.23. а) , ;
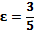б) 
, 
;
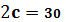в) 
.
4.24. а) , 
;
б) 
, ;
в)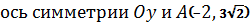 
.
4.25. а) , 
;
б) 
, 
;
в) 
.
4.26. а) , 
;
б) , ;
в) 
.
4.27. а) 
, 
;
б) , 
;
в) .
4.28. а) 
, 
;
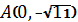б) 
, 
;
в) 
.
4.29. а) , 
;
б) 
, 
;
в) 
.
4.30. а) 
, 
;
б) 
, ;
в) 
.
Записать уравнение окружности, проходящей через указанные точки и имеющей центр в точке.
Варианты:
5.1. Вершины гиперболы 
, .
5.2. Вершины гиперболы 
, 
.
5.3. Фокусы гиперболы 
, 
.
5.4. 
, - вершина параболы 
.
5.5. Фокусы эллипса , 
.
5.6. Левый фокус гиперболы , 
.
5.7. Фокусы эллипса , - его верхняя вершина.
5.8. Вершину гиперболы 
, .
5.9. Фокусы гиперболы , 
.
5.10. , - вершина параболы 
.
5.11. Правый фокус эллипса 
, 
.
5.12. Левый фокус гиперболы 
, .
5.13. Фокусы эллипса 
, - его нижняя вершина.
5.14. Вершину гиперболы , .
5.15. Фокусы гиперболы 
, 
.
5.16.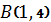 
, - вершина параболы 
.
5.17. Левый фокус эллипса , 
.
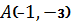5.18. Левую вершину гиперболы , 
.
5.19. Фокусы эллипса 
, - его верхняя вершина.
5.20. Правую вершину гиперболы 
, 
.
5.21. Левый фокус гиперболы 
, 
.
5.22. 
, - вершина параболы 
.
5.23. Правый фокус эллипса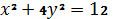 
, 
.
5.24. Правую вершину гиперболы 
, 
.
5.25. Фокусы эллипса 
, - его нижняя вершина.
5.26. Правую вершину гиперболы 
, 
.
5.27. Фокусы гиперболы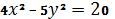 
, .
5.28. 
, - вершина параболы 
.
5.29. Левый фокус эллипса 
, 
.
5.30. Правый фокус гиперболы 
, 
.
