Классификация измерительных сигналов

ДЕ 1. Теоретические основы метрологии

Измерительные сигналы

1. Классификация измерительных сигналов (аналоговые, дискретные, цифровые и.т.д.) и помех (по месту возникновения, по основным свойствам и др).

2. Математические модели элементарных измерительных сигналов.

 

Классификация измерительных сигналов

Сигналом называется материальный носитель ин­формации, представляющий собой некоторый физи­ческий процесс, один из параметров которого функ­ционально связан с измеряемой физической величи­ной. Такой параметр называют информативным.

Измерительный сигнал — это сигнал, содержащий количественную информацию об измеряемой физи­ческой величине. Их классифика­ция по различным признакам приведена на рис. 1.

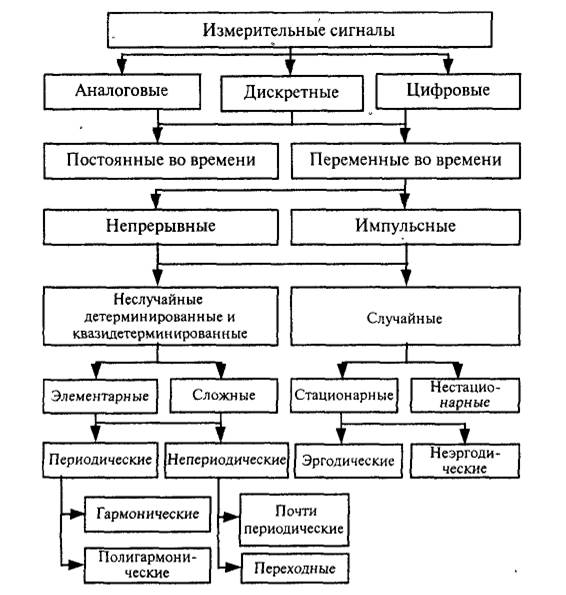
Рис. 1. Классификация измерительных сигналов

 

По характеру измерения информативного и времен­ного параметров измерительные сигналы делятся на аналоговые, дискретные и цифровые.

Аналоговый сигнал — это сигнал, изменяющейся непрерывно во времени и могут принимать любые значения на некотором интервале. Аналоговые сигналы описываются некоторой математической функцией времени. Пример АС — гармонический сигнал — s(t) = A·cos(ω·t + φ).

Дискретный сигнал — это сигнал, который представляется в виде последовательности значений, взятых в дискретные моменты времени. Эти значения называются отсчётами. Δt называется интервалом дискретизации.

Цифровые сигналы — квантованные по уровню и дискретные по времени сигналы Y_ц(nT), которые описываются квантованными решетчатыми функциями (квантованными последовательностями), принимающими в дискретные моменты времени nТ лишь конечный ряд дискретных значений — уровней кван­тования h₁, h₂,..., h_n (рис. 2, в).

Квантованный сигнал. При квантовании вся область значений сигнала разбивается на уровни, количество которых должно быть представлено в числах заданной разрядности. Расстояния между этими уровнями называется шагом квантования Δ.

Цифровые сигналы — квантованные по уровню и дискретные по времени сигналы. На каждом заданном промежутке времени известно приближённое (квантованное) значение сигнала, которое можно записать целым числом. Если записать эти целые числа в двоичной системе, получится последовательность нулей и единиц, которая и будет являться цифровым сигналом.

 

 

По характеру изменения во времени сигналы де­лятся на постоянные, значения которых с течением времени не изменяются, и переменные, значения ко­торых меняются во времени. Постоянные сигналы являются наиболее простым видом измерительных сигналов.

Переменные сигналы могут быть непрерывными во времени и импульсными. Непрерывным называется сигнал, параметры которого изменяются непрерывно. Импульсный сигнал — это сигнал конечной энергии, существенно отличный от нуля в течение ограничен­ного интервала времени, соизмеримого с временем завершения переходного процесса в системе, для воз­действия на которую этот сигнал предназначен.

По степени наличия априорной информации пере­менные измерительные сигналы делятся на детерми­нированные, квазидетерминированные и случайные.

Детерминированный сигнал — это сигнал, закон изменения которого известен, а модель не содержит неизвестных параметров. Мгновенные значения де­терминированного сигнала известны в любой момент времени. Детерминированными (с известной степе­нью точности) являются сигналы на выходе мер. На­пример, выходной сигнал генератора низкочастотно­го синусоидального сигнала характеризуется значе­ниями амплитуды и частоты, которые установлены на его органах управления. Погрешности установки этих параметров определяются метрологическими харак­теристиками генератора.

Квазидетерминированные сигналы — это сигналы с частично известным характером изменения во време­ни, т.е. с одним или несколькими неизвестными па­раметрами. Они наиболее интересны с точки зрения метрологии. Подавляющее большинство измеритель­ных сигналов являются квазидетерминированными.

Детерминированные и квазидетерминированные сигналыделятся на элементарные, описываемые про­стейшими математическими формулами, и сложные. К элементарным относятся постоянный и гармониче­ский сигналы, а также сигналы, описываемые единичной и дельта-функцией. К сложным сигналам относятся импульсные и моду­лированные сигналы.

Сигналы могут быть периодическими и непериоди­ческими. Непериодические сигналы делятся на почти периодические и переходные. Почти периодическим называется сигнал, значения которого приближенно повторяются при добавлении к временному аргументу надлежащим образом выбранного числа — почти пе­риода. Периодический сигнал является частным слу­чаем таких сигналов. Почти периодические функции получаются в результате сложения периодических функций с несоизмеримыми периодами. Переходные сигналы описывают переходные процессы в физиче­ских системах.

Периодическим называется сигнал, мгновенные значения которого повторяются через постоянный интервал времени. Период T сигнала — параметр, рав­ный наименьшему такому интервалу времени. Час­тота f периодического сигнала — величина, обратная периоду. Периодический сигнал характеризуется спектром. Различают три вида спектра:

• комплексный — комплексная функция дискрет­ного аргумента, кратного целому числу значений час­тоты ω периодического сигнала Y (t), представляющая собой значения коэффициентов комплексного ряда Фурье:

где k — любое целое число;

• амплитудный — функция дискретного аргумен­та, представляющая собой модуль комплексного спек­тра периодического сигнала:

где Re(z), Im(z) — действительная и мнимая части комплексного числа z;

• фазовый — функция дискретного аргумента, представляющая собой аргумент комплексного спек­тра периодического сигнала:

Периодической сигнал содержит ряд гармоник. Гармоника — гармонический сигнал с амплитудой и начальной фазой, равными соответствующим значе­ниям амплитудного и фазового спектра периодиче­ского сигнала при некотором значении аргумента. Наличие высших гармоник в спектре периодического сигнала количественно описывается коэффициентом гармоник, характеризующим отличие формы данного периодического сигнала от гармонической (синусои­дальной). Он равен отношению среднеквадратического значения сигнала суммы всех его гармоник, кроме первой, к среднеквадратическому значению первой гармоники:

где Y,, У, — i-я и первая гармоники сигнала Y (t).

Периодические сигналы бывают гармоническими, т. е. содержащими только одну гармонику, и полигар­моническими, спектр которых состоит из множества гармонических составляющих. К гармоническим сиг­налам относятся сигналы, описываемые функцией синуса или косинуса. Все остальные сигналы являют­ся полигармоническими.

Случайный сигнал — это изменяющаяся во време­ни физическая величина, мгновенное значение кото­рой является случайной величиной.

Эргодическим называется сигнал, вероятностные характеристики которого не зависят от номера реализации.

Классификация помех

Измерительные сигналы редко присутствуют в средствах измерений в чистом виде. Практически все­гда на них накладываются помехи.

Под помехой по­нимается сигнал, однородный с измерительным и действующий одновременно с ним. Его присутствие приводит к появлению погрешности измерения. Классификация помех возможна по ряду признаков.

По месту возникновения помехи делятся на внеш­ние и внутренние. Причиной возникновения внешних помех являются природные процессы и работа раз­личных технических устройств. Последние создают так называемые индустриальные помехи. Внутренние помехи обусловлены процессами, происходящими при работе самого средства измерений.

В зависимости от вида включения источников по­мехи и измерительного сигнала в эквивалентных схе­мах средств измерений различают помехи общего вида (синфазные) и помехи нормального (последователь­ные) вида.

Источник помехи общего вида включен между общими точками (корпусами) схем объекта измерений и СИ. Источник помехи нормального вида включен последовательно во входную цепь СИ.

По виду частотного спектра помехи делятся на бе­лый и розовый шумы. Спектральные составляющие бе­лого шума равномерно распределены по всему частот­ному диапазону. У розового шума спектральная мощность, приходящаяся на декаду частоты, постоянна.

По основным свойствам помехи можно разделить на три вида: флуктуационные, сосредоточенные и импульсные.

Флуктуационные помехи представляют собой хаоти­ческое, беспорядочное изменение во времени сигнала, однородного с измеряемым, в каком-либо месте средст­ва измерений. Такие помехи часто называют шумом.

Пример — внутренние шумы измерительных электрон­ных усилителей. Различают следующие виды шумов:

• тепловой (шум Джонсона), по своим свойствам близкий кбелому шуму. Тепловой шум генерируется любым резистором, находящимся в измерительной цепи. Значение его состоит в том, что он устанавлива­ет нижнюю границу напряжения шумов любого изме­рительного преобразователя, имеющего выходное со­противление;

• дробовый, обусловленный движением электро­нов — дискретных носителей электрического тока. Он имеет равномерный спектр, т. е. является белым;

• фликкер-шум. К данному виду относят шумы, у которых спектральная мощность на декаду частоты примерно постоянна, т. е. розовые шумы, например шум постоянного резистора, пропорциональный про­текающему через него току, шум тока базы транзи­стора и др.

Влияние флуктуационной помехи уменьшается при усреднении суммы измерительного сигнала и по­мехи. Максимальное уменьшение влияния флуктуационной помехи на результат измерения возможно в том случае, когда спектральная плотность помехи по­стоянна в пределах полосы пропускания средства измерений, т.е. помеха имеет характер белого шума.

Сосредоточенными называют помехи, основная часть мощности которых сосредоточена на отдельных участках диапазона частот, меньших полосы пропус­кания СИ. Помехи, наводимые в измерительных це­пях СИ от промышленной силовой сети частотой 50 Гц, являются сосредоточенными. Эффективность их подавления в значительной мере определяется дос­товерностью априорных данных о частотном спектре.

Импульсными помехами называется регулярная или хаотическая последовательность импульсных сигна­лов, однородных с измерительным сигналом. Источниками таких помех являются цифровые и коммутируюшие элементы СИ или работающего рядом с ними устройства. Характерный пример импульсных помех — помехи от устройств зажигания двигателей внутрен­него сгорания. Импульсные и сосредоточенные поме­хи часто называют наводками.

Поскольку основным следствием действия поме­хи является появление погрешности измерения, то стараются устранить или, по крайней мере, ослабить их действие на средства измерений. Для устранения влияния помех целесообразно, если это возможно, ис­ключить причины их возникновения. Способы борьбы с помехами в значительной мере зависят от их спек­трального состава, вида измерительного сигнала и помехи.