Теоретические положения
Твердые тела под действием внешних сил деформируются, то есть изменяют свои размеры и форму. Деформация, исчезающая при прекращении действия внешних сил, называется упругой.
К концам стержня, изображенного на рисунке 8.1, приложены направленные вдоль его оси в противоположные стороны силы 
, действие которых равномерно распределено по всему сечению стержня. В результате упругой деформации длина стержня изменится на величину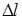 
. Относительное изменение длины стержня будет равно
,
где 
– длина недеформированного стержня.
Опытные данные показывают, что
 ,
| (8.1) |
где S – площадь поперечного сечения стержня;
E – модуль Юнга;
– нормальное напряжение.
Модуль Юнга E является важной физической величиной, характеризующей упругие свойства материала, и не зависит от геометрических размеров и формы тела. В СИ модуль Юнга выражается в паскалях (1 Па = 1 Н/м2).
Выражая из формулы (8.1) силу F, получаем:
,
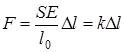где 
– коэффициент упругости стержня.
Это выражение называют законом Гука для деформаций растяжения и сжатия стержней.
 |
Балка, изображенная на рисунке 8.2, одним концом жестко закреплена в вертикальной опоре. К другому концу балки приложена направленная вертикально вниз сила F. В результате действия этой силы произойдет изгиб балки, при этом ее свободный конец, к которому приложена сила F, сместится вниз на расстояние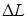 
.
Теоретический анализ [1] показывает, что значение 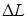для балки длиной l, имеющей круговое поперечное сечение диаметром d, можно найти по формуле
.
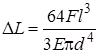Тогда для модуля Юнга получаем
 ,
| (8.2) |
Таким образом, можно экспериментально определить модуль Юнга материала, из которого выполнена балка, если измерить смещение 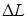конца балки под действием силы F.
Экспериментальная установка
В лабораторной работе экспериментально определяется модуль Юнга материала балок, имеющих круговое поперечное сечение. Схема экспериментальной установки изображена на рисунке 8.3.
С помощью зажима балка закрепляется в горизонтальном положении на стойке установки. К концу балки с помощью нити подвешивается груз массой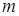 
. На балку со стороны нити будет действовать сила
 ,
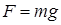| (8.3) |
где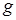 
– ускорение свободного падения.
Действие силы 
приведет к изгибу, в результате которого конец балки сместится на расстояние 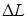. Подставляя значение силы из выражения (8.3) в зависимость (8.2), получаем расчетную формулу:
 ,
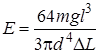| (8.4) |
Порядок выполнения работы и обработки результатов измерений
1. ознакомиться с устройством экспериментальной установки, записать перечень приборов и принадлежностей и их характеристики в отчет о лабораторной работе.
2. Выполнить опыты поочередно с двумя балками, выполненными из различных материалов. Для этого закрепить одну из балок в горизонтальном положении на стойке установки. С помощью линейки измерить длину l балки и расстояние 
от конца балки до основания стойки. На конце балки закрепить нить с подвесом массой m, после чего вновь измерить расстояние (
) от конца балки до основания стойки. Определить смещение конца балки
и рассчитать модуль Юнга материала балки по формуле (8.4).
Повторить измерения не менее четырех раз, устанавливая на подвес дополнительные грузы. Полученные данные записать в таблицу 8.1, а затем выполнить аналогичные опыты со второй балкой.
Можно выполнять опыты, не меняя массу груза, подвешенного к концу балки, но изменяя ее длину l.
Таблица 8.1 – Результаты измерений
| Материал балки | Номер опыта | l | m | L 0 | L | D L | E |
3. Рассчитать среднее арифметическое полученных значений модуля Юнга для каждой из балок.
4. Оценить случайную абсолютную и относительную погрешность измерения модуля Юнга одной из балок.
5. Сравнить полученные опытные данные со справочными данными, приведенными в таблице Б.1 приложений.
6. Проанализировать полученные результаты.
Контрольные вопросы
1. Какую физическую величину называют модулем Юнга?
2. Функцией каких величин является коэффициент упругости стержня при растяжении и сжатии?
*Аникин А.И. Механика: методические указания к выполнению лабораторных работ по физике / А.И. Аникин – Архангельск: Изд-во АГТУ, 2008. – 49 с.
