Сформулировать и доказать теорему о полноте исчисления высказываний.

Теорема: Если , то в исчислении высказываний . Доказательство: Поскольку , то по лемме при любых значениях σ₁,σ_2,…,σ_n.Если σ₁=1, то , а при σ₁=0 мы имеем что 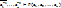. Гипотеза оказывается не существенной, и, удаляя её по теореме мы получаем, что . Удаляя тем же образом по очереди все остальные гипотезы, видим что .

1.11. Правило резолюций. Метод резолюций в ИВ. В двузначной логике имеет место формула: (xvy)( vz)=(xvy)( vz) (yvz)-резольвента. Th о методе резолюций в ИВ: Из F₁,F₂,…,F_n├F↔ F₁,F₂,…,F_n, ≡0, F₁,F₂,…,F_n├F ↔├F₁→(F₂→…(F_n→F)…) ↔F₁→(F₂→…→(F_n→F)…)≡1 ↔ v v…v vF≡1 ↔ ≡0 ↔F₁,F₂,…,F_n ≡0.

1.12. Некаузальное правило резолюции. Th:Если дана A(x) B(x)=A(x) B(x) (A(0) B(1)). Разбор случаев по x: x=0 LP=A(0) B(0). RP=A(0) B(0) (A(0) B(1))=A(0) B(0) A(0) B(0) B(1)=A(0) B(0)

1.13. Исчисление предикатов: Опр: Для исчисления предикатов необходимо задать: 1) Алфавит: x₁,x₂…x_n-предметные переменные, –функциональная переменная, a₁,a₂…a_n-предметные постоянные, →,┐,(,), -дополнительные символы. 2) Термы: x_i,a_i-термы. Если -функц.переменная, то (t₁,t₂…t_n)-терм,где t_i-термы. 3) Формулы: Если t₁,…,t_n термы, то (t₁,t₂…t_n)-формула. Если F₁ и F₂ формулы, то ₁, ₂,F₁→F₂-ф-лы. Если F(x)-формула, то x F(x), x F(x) – формулы.. предметная переменная x может входить в формулу свободно или связанно. В термах все входящие переменные являются свободными. В ф-ле (t₁,…,t_n) все переменные являются свободными. Пишем F(x) если x входит в F свободно. Кванторы связности переменных, т.е. xF(x) x-связ. xF(x)x-связ. 4) Аксиомы: A1,A2,A3 – аксиомы в ИВ, P1= xF(x)→F(t) где t-переменная, P2=F(t)→ xF(x). 5) Правило вывода MP: где А и В – ф-лы. - I , где G - формула не зависящая от x. - I

1.14. Теорема о подстановке терма и теорема о переименовании связанной переменной. Th1: В ИП F(x)=> F(t), где t-терм. 1) F(x) дано; 2) Let G не зависит от x; 3) F(x)→(G→F(x)) акс A1; 4) G→F(x) (MP к 1 и 3); 5) G→ xF(x) правило введения квантора всеобщности; 6) xF(x) (MP к 2 и 5); 7) xF(x)→F(t) акс P1; 8) F(t) (MP к 6 и 7); Th2: О переименовании связ.переменных xF(x)=> AyF(y); 1) xF(x) – дано; 2) xF(x)→F(y) акс P1; 3) xF(x)→ yF(y) I (2); 4) yF(y) (MP к 1 и 3).

1.15. Интерпретация и непротиворечивость ИП. При интерпретации ИП задается некоторое множество M. При этом предметная постоянная a_i M, предметная переменная x_i M; Ф-ии y=f(x₁,…x_n) рассмотрим на M x_i,y M; Предикатным символам P отвечают предикаты на M: y=P(x_i,…x_n) x_i M, y {0;1} => терм принимает значения в M. ф-ла ИП становится формулой 2-значной логики. Th: Если F в ИП, то ф-ла F≡1 при любой интерпретации, т.е. для м-ва M.; Доказать А1-А3; P1= xF(x)→F(t); 1) xF(x)=1=>F(x)≡1 x M => F(t)=1 в частности xF(x)→F(t)=1→1=1; 2) xF(x)=0; P1=0→F(t)=1 (из-за лжи следует всё, что угодно, за это она верна всегда); P2=F(t)→ xF(x); 1) xF(x)=0=> F(x)≡_M 0 => F(t)=0 т.к. t M; P2=0→0=1; 2) xF(x)=1 тогда акс P2=F(t)→1=F(t) 1≡1; Правила вывода: I :Let G→F(x)≡1. Требуется доказать, что G→ xF(x)=1; 1)Пусть G=0, тогда G→ xF(x)=0→ xF(x)=1; 2)G=1, по условию G→F(x)≡1; 1→F(x)≡1; 0 F(x)≡1=>F(x)≡1 => xF(x)=1 => G→ xF(x)=1→1=1; I : ; I :Let F(x)→G≡1. Требуется доказать, что xF(x)→G=1; 1) G=0 F(x)→0≡1 => F(x)≡0 => xF(x)=0 тогда xF(x)→G=0→0=1; 2) G=1. Тогда xF(x)→C= ; Доказать MP.;

1.15. Интерпретация и непротиворечивость. Th о непротиворечивости ИП: Нет такой формулы F, чтобы . От противного: Если бы F => Th об интерпретации => ; Th о полноте ИП. Если при интерпретации M F≡1 в интервале M, то F в ИП.

1.16. Метод резолюции в ИП. Эрбранова область. Th дедукции для ИП: Г А→В => Г,А В аналогично в ИВ. Th о методе резолюций: F₁ F₂ … F_n ≡0 Это для M => F₁,F₂,…F_n в ИП аналогично в ИВ. Оказывается, достаточно доказать, что G=F₁ F₂ … F_n ≡0 для множества H – эрбранова обл. H строится так: 1) Правило G к сколемовской форме: G= x₁ x₂… x_k P(x_1,x₂…x_k); 2) Если в ф-ле G имеется const C_i то C_i H; Если в ф-ле G нет const, то заводим константу С H; Если в ф-ле G учавствует ф-ия f, то для h₁,…h_n H => y=f(h₁,…h_n) H.

1.17. Дать определение исчисления с равенством. Сформулировать и доказать три свойства равенства. Конкретные аксиоматич теор получ из исчисления предикатов добавл-ем собственных аксиом, предметных констант, предикатных и функциональных символов. Пример: рассмотрим аксиоматическую теорию с равенством (EQ). К исчислению предикатов добавим конкретный предикат Р(х,у), который обозначим через х=у и две новые аксиомы: Еq1 х (х=х), Еq2 (х=у) (F(х) F(x//у)), где частичная подстановка F(х//у)) означ правильн замену в формуле некоторых вхождений переменой х на переменную у. Свойство 1. В теории с равенством t= t, где t – терм. Доказательство состоит из следующих утверждений: ⊢ х(х = х) – аксиома Eq1; ⊢ х(х = х) (t = t) – аксиома Р1 исчисления предикатов; ⊢ (t = t) – из 1) и 2) по правилу modus ponens. Свойство 2. В теории EQ имеет место симметричность равенства, т.е. х = у ⊢ у = х. Доказательство состоит из следующих утверждений: 1) ⊢(х = у) ((х = х) (у = х)) – аксиома Eq2, в которой в качестве F(x) взяли формулу х = х; 2) х = у ⊢ (х = х) (у = х) – из 1) по теореме деукции; 3) х = у, х = х⊢ у = х – из 2) по тоеореме дедукции; 4) ⊢ х = х – по свойству 1; 5) х = у⊢ у = х – из 3) удалением выводим гипотезы х = х. Свойство 3. В теории EQ имеет место транзитивность равенства, т.е. х = у, у = z ⊢x = z. Доказательство состоит из следующих утверждений: 1) ⊢ (у = х) ((у = z) (х = z)) – аксиома Еq2, в которой в качестве F(у) взяли формулу у = z; 2) у = х⊢ (у = z) – из 1) по теореме дедукции; 3) х = у ⊢ у = х – по свойству 2; 4) х = у ⊢ (у = z) (х = z) – из 3) и 2) по транзитивности вывода; 5) х = у, у = z ⊢ х = z – из 4) по теореме дедукции.

1.18. Дать определение формальной арифметики. Сформулировать теорему Геделя о неполноте. Формальная арифметика получается из теории с равенством добавлением константы 0, введением функциональных символов. f(x,y) = x + y, g(x,y) = xy, next(x) = x’ и добавлением следующих собственных аксиом: (Ar1) F(0) ( х (F(x) F(x’)) x F(x)), (Ar2) (t’₁ = t’₂) (t₁= t₂), (Ar3) (t₁ = t₂ ) (t’₁= t’₂), (Ar4) t’ 0, (Ar5) t + 0 = t’, (Ar6) t₁ + t’₂ = (t₁ + t₂)’, (Ar7) t·0 = 0, (Ar8) t₁· t’₂ = t₁ · t₂ + t₁. Аксиому Ar1 называют принципом математической индукции. Приведем другую формулировку этого принципа. Свойство 1. Если ⊢ F(0) и ⊢ F(x) F(x)’, то ⊢ х F(x). Доказательство состоит из следующих утверждений: 1) ⊢ F(x) F(x)’ – дано по условию; 2) ⊢ х(F(x) F(x’)) – из 1) по правилу обобщения; 3) ⊢F(0) – дано по условию; 4) ⊢F(0) ( F(x) F(x’)) x F(x)) – аксиома Ar1, 5) ⊢ x (F(x) F(x’)) x F(x) – из 3) и 4) по правилу MP, 6) ⊢ x F(x) – из 2) и 5) по правилу MP. Свойство 1 доказано. Моделью для формальной арифметики является множество N^u обычными операциями сложения и умножения, а next(x) = х + 1. В отличие от исчисления высказываний и исчисления предикатов формальная арифметика не является полной. Мы приведем без доказательства формулировки теоремы о ее неполноте. Теорема Геделя о неполноте. Существует замкнутая формула F такая, что в формальной арифметике не выводиться как формула F, так и ее отрицание .

1.19. дать определение дизьюнкции, коньюнкции и отрицания в нечеткой логике. доказать в нечеткой логике, что a v (b с) = (а V b) ∧ (a V c) и = V . В нечеткой логике рассматриваются функции у=f(x₁,…, x_n),где X_i [0;1] при i= 1,2, …., n и у [0;1]. Определение 1. Значения нечеткой дизьюнкции и коньюкции определяется по формуле у= х₁Vх₂=max(x₁,x₂) и у = x₁∧x₂= min(x₁,x₂). Следующие свойства нечеткой дизьюнкции и коньюнкции такие же, как и для двузначной логики: 1)a V 0 = a; 1’) a ∧ 0 = 0; 2) a V 1 = 1; 2’) a ∧ 1 = a; 3) a V a = a; 3’) a ∧ a = a; 4) a V b = b V a; 4’) a ∧ b = b ∧ a; 5) a V (b V c) = (a V b) V c; 5’) a∧ (b ∧ c) = (a ∧ b) ∧ c; 6) если a b, то a V c b V c; 6’) если a b, то a ∧ c b ∧ c; 7)a ∧ (b V c) = (a ∧ b) V (a ∧ c); 7’) a V (b ∧ c) = (a V b) ∧ (a ∧ c). Свойства 1 – 6 и 1’ – 6’ непосредственно вытекают из определения: приведем доказательство свойства 7. Пусть b c, тогда a ∧ (b V c) = a ∧ c и (a ∧ b) V (a ∧ c) = a ∧ c, т.к. a ∧ b a ∧ c по свойству 6’. Свойство 7’ доказывается аналогично. Определение 2. Значение нечеткого отрицания определяется по формуле у= =1- х. Следующие св-ва нечеткого отрицания совпадают со свойствами отрицания в двузначной логике: 1) = 1, 2) = 0, 3) = a, 4) a b, то , 5) = ∨ , 6) = ∧ Доказательство свойств 8 – 11 очевидно; докажем свойство 12. Пусть a b, тогда = , так как a ∧ b = a; a ∨ = потому, что b. Св-во 13 доказывается аналогично. Определение 3. Функция у = х ∧ называется противоречием, обозначается у = . Из этого определения вытекают следующие св-ва: = 15) Определение 4. Функция у = х ∨ называется тавтологией, обозначается у = . Из этого определения вытекает следующие св-ва: = 17) Заметим, что в двузначной логике х ∧ 0, а х V 1, что не имеет места в нечеткой логике. Определение 5. Функция у = f(х) называется противоречивой, если f(х) для всех х Примером противоречивой функции является у = . Определение 6. Функция у = f (х) называется общезначимой, если f (х) для всех х . В качестве примера общезначимой функции можно привести тавтологию у = .

1.20. Дать определение нечеткой импликации и эквивалентности. Доказать в нечеткой логике, что a b = (a ∧ b) V ( ∧ ). Определение 1. Нечеткая импликация определяется по формуле а b = V b. Из этого определения вытекают следующие свойства: 1) 0 a = 1, 2) a 1 = 1, 3) a a = ∨ a = Определение 2. Нечеткую эквиваленцию можно определить по формуле а b = (a b) ∧ ( a). Отметим следующие св-ва нечеткой эквиваленции: a b = ( ∨ b) ∧ ( ∨ a), a a = V a = , a b = (a ∧ b) ∨ ( ∧ ). Докажем свойство 6. Для этого разберем два случая. 1) Пусть a , тогда b, из них выводится, что ∧ b) ∧ (a ∨ ) = ∧ ⟹ a b = ∧ . С другой стороны, ∧ ⟹ (a ∧ b) ∨ ( ∧ ) = ∧ , следовательно, a = (a ∧ b) V ( ∧ ). 2) Случай a разбирается аналогично. Замечание. Можно ввести в нечеткой логике и остальные логические операции по формулам х ⊕ у = – “ исключающие или “, х ⎡у = ∨ - штрих Шеффера, х ↓у = ∧ - стрелка Пирса.

1.21. Дать определение нечеткого множества и операций дополнения, пересечения, объединения, возведения в степень, умножения и сложения нечетких множеств. Доказать, что A B ⊂ A + B.

Нечеткое значение высказывания Р будем обозначать µ(Р). Определение 1. Множество А называется нечетким, если задана функция принадлежности, которая по любому его элементу х определяет число µ_А(х) = µ(х [0;1], равное нечеткому значению предиката х U\ А, где U – универсум, считается по умолчанию, что µ_А(х) = 0. Пример 1. Зададим нечеткие множества А и В таким образом: А = /х₁, 1/х₂, 0.8/х₃, 0/х_{4 ,} В = ; из этой записи следует, что µ_А(х₁) = 0.3, µ_А(х₂) =1, µ_В(х₁) = 0 и т.д.. Определение 2. Для нечетких множеств можно определить отношения равенства и подмножества: А = В, если х(µ_А(х) = µ_В(х)); А ⊂ В, если х(µ_А(х) µ_В(х)). Заметим, что, если х(µ_А(х) = 0), то множество А считается пустым, А = ∅. Определение 3. Функции принадлежности для дополнения, пересечения и объединения нечетких множеств определяется так: (х)= 1- (х), = ∧ = min (, (x) = V (x) = max ( (x), (x)). Из определений 2, 3 и свойств отрицания, коньюнкции и дизьюнкции следует, что на нечеткие множества переносятся обычные свойства операций дополнения, пересечения и объединения. Отметим некоторые из этих свойств. 1) А А = А. 1’) A A = A. 2) А (В С) = (А В) (А С). 2’) A (B C) = (A ) (A C). 3) = . 3’) = . Определение 4. Введем операции возведения в степень, умножения и сложения нечетких множеств, задавая их функции принадлежности таким образом: (x) = (x) при n 0, (x) = (x) · (x), (x) = (x) + (x) - (x) · (x). Отметим некоторые свойства введенных операций. 1) ⊂ A при n 1. 1’) A ⊂ при n 1. 2) ·B ⊂ A B. 2’) A B ⊂ A + B. 3) = + . 3’) = · . Пример 2. Если А и В – множества, данные в примере 1, то А В = А В = , = А· В = ,А+В = Пример 3. Пусть нечеткие значения предикатов р = (х А), q= (x B) и r = (x C) следующие: р = 0,2, q = 0,4 и r = 0,7. Найти нечеткое значение предиката s = (x Решение. Поскольку s = ∧ (q V r), то подставляя значения p,q,r, получаем, что s = 0,8 ∧ (0,4V0,7) = 0,8 ∧ 0,7 = 0,7. Ответ. Нечеткое значение предиката s равно 0,7.