Тасқын жағдайына анализ жасаумен Ньютон, Эри, Лаплас, Джордж Дарвин(Чарльз Дарвиннің ұлы), Кельвинды қоса санағанда бұрынғының көптеген математиктері мен физиктері айналысқан. Бұл жерде құбылысты түсіндіру үшін Ньютонның физикалық теориясы қолданылады. Дегенмен де, гармониялық талдаулардың математикалық тәсілдері негіз болатын заманауи талдау мен тасқындарға алдын-ала болжам жасау Лорд Кельвиннің Глазгода жасаған іргелі жұмыстарына негізделетінін ескере кеткен жөн. Мұхиттардағы сұйықтық айналмалы жер қабатында гравитация күшімен ұсталып отырады. Жердің Күн және Аймен өзара гравитациялық қозғалысы тасқындарды тудыра отырып, бұл күштерге қарсы тұрады. ТЭЦ турбинасынан алынатын тасқын энергиясы тасқынды процесс кезінде су ағып өтетін айналмалы жердің кинетикалық энергиясының бір бөлігін тартып алады. Егер бүкіл әлемдегеі қаншама болмасын жеткілікті жоғары дәрежедегі тасқындарды іске асыратын болсақ, онда есептеулер бойынша ол Жердің өз осінен айналу периодын 2000 жылда 1 тәулікке қысқартады. Бұл қоршаған ортаға айтарлықтай зиян келтірмейді.
13.1 сурет Жер мен айдың салыстырмалы қозғалысы. Айналым ω жиілікпен О нүктесінің айналасында жүреді, L'=4670 км.
13.2 сурет тіуліктік және жарты тәуліктік тасқындардың болуынының физикалық негіздемесі. Айдың Жер экваторының жазықтығындаорналасу кезіндегі тепе-теңдік қалпындағы тасқындардың қысқаша анықтамасы. Р нүктесінде бірдей тасқындар тәулігіне 2 рет кездесуі – ол жарты тәуліктік тасқындар(а). Әдетте Ай Жердің экваторлық жазықтығында жатпайды. Сондықтан Р нүктесіндегі тасқындар тәулігіне 1 рет пайда болады – олар тәуліктік тасқындар (б).
Айдың әсерінен туындайтын тасқындар. Жер мен Ай ғарыш кеңістігінде бірін-бірі айнала қозғалады. (13.1 сурет), бірақ Жердің массасы Ай массасынан шамамен 100 есе үлкен болғандықтан, Айдың қозғалысы Жердікіне қарағанда айқын болады. Бұл айналымның центрі О нүктесінде орналасқан, ол үшін ML = M'L' теңдігі дұрыс болып саналады.
Осылайша,
L' = MD / (M' + M) (13.1)
Cонымен L' = 4670 км, ал Жердің орташа радиусы 6371 км-ге тең, онда O центрі Жер шарының ішкі қабатында жатады. Айдың Жерден артта қалуы өзара гравитациялық қозғалыс пен ортадан тепкіш күштердің есебінен қолдау тауып отырады. Егер гравитациялық тұрақтыны G деп белгілесек, онда
GMM' / 
= 
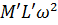= ML 
(13.2)
Егер де Жердегі барлық массаны оның Е центріне орналастырсақ, онда әрбір масса элементі Айға қатысты бірқалыпты күйде болған болар еді. Бірақ Жер массасы Е нүктесінің айналасында орналасқан, және оның барша элементіне әр түрлі күш әсер етеді. Осылайша, Y нүктесінде орналасқан элемент, айналу радиусының r + L' ұзындығына дейін ұлғаюынының әсерінен Айдың тарапанын болатын тартылыс күшінің азаюын және ортадан тепкіш күшінің ұлғаюын бастан кешеді(13.1 - сурет). Айға ең жақын элемент өзіне қарай бағытталған тартылыс күшінің ұлғайғанын байқайды, оған әсер ететін ортадан тепкіш күш айналу радиусының r - L' шамасына дейін кішіреуінің әсерінен азаяды. Жердің қатты жыныстары Айдың айналуы кезінде осы күштердің өзгеруін байқай отырып, тек салыстырмалы түрде аздаған деформацияға ұшырайды (созғыш және сыққыш күштер ішкі кернеу арқылы өтіледі). Сұйықтықта мұндай кернеулер туындамайды және де ол Жердің кеңістігіне қатысты қозғалысқа түседі. Бұл су тасуының себебі болып табылады.
Егер де Ай Жердің экваторлық жазықтығында орналасса, онда мұхит сулары Айда максималды алшақ және жақын жатқан x және y нүктелерінде шектік мәнге жетуге тырысады. Жердің қатты жыныстары бұл шектік нүктелерде 24 сағат периодпен айналады. (13.2 а сурет). Осылайша кез-келген тоған басқа эффектілерді есепке алмағанда, Жер бетіндегі қолайлы жағдайларда орналасқан жазықтықтан өткен кезінде су деңгейінің көтерілуі мен төмендеуін 2 есе өткеретін болады. Бұл – жарты тәуліктік тасқындар. Жердің өз осінен тәуліктік айналуы тасқын биіктігіне әсерін тигізбейді. Айдың тарту күші мен Айдың ω жиілікпен айналу кезіндегі О нүктесіне қатысты ортадан тепкіш күшін біле отырып (13.1 сурет), тасқынды тудыратын қорытынды күшті бағалауға болады. Айдан Y нүктесінде алшақтаған m су массасы үшін
=m(L' + r) – GMm / 
(13.3)
Айға жақын х нүктесі үшін:
= m(r - L') + GMm /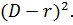 
(13.4)
Анықтама бойынша (13.1 - сурет)
GMm / = mL' 
(13.5)
Бірақ r << D болғандықтан
1 /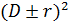 
= (1 ± 2r / D) / . (13.6)
(13.5) және (13.6) формулаларын (13.3) және (13.4) формулаларына қою арқылы аламыз:
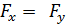= mr (1 + 2L' / D). (13.7)
Осылайша бірдей амплитудағы екі тасқын шыңын күнделікті байқап отыру керек. Сөзсіз бұл Айдың Жер экваторы жазықтығында орналасу жағдайы үшін тек үлкен мұхиттарда ғана орын алады. Осы тепе-теңдік моделіне сәйкес судың төмен деңгейі кезінде (отлив) сұйықтықтың бөлшектеріне әсер етуші күш mr тең. Осылайша,(13.7) тасқан тудыру күші mr 
болады. Осы күш есебінен алынатын судың бірсарынды максимал көтерілуі (тасқынның тепе-теңдік биіктігі) 0.36 метрге тең. Тепе-теңдік қалпындағы тасқынның қарапайым моделі мен тасқынның нақты жағдайларының ерекшеліктерінің 3 негізгі себептері бар.
1. Бұл модельде тасқын тудырушы күштердің қимылына берілетін түсініктемелер физикалық тұрғыдан дұрыс. Алайда, тасқын шыңының Жер айналымын қадағалай отырып, үлкен мұхиттарда 1600 км/сағ жылдамдықпен ауысатындағы қате. Шыңдығында тасқынды толқын Айдың меридианында бола тұра мұндай жоғары жылдамдықпен қозғала алмайды (13.3 есептеуінен қараймыз). Айдың мұхит үстінен өту кезінде тасқынды қозғалыс бар болғаны 500 км/сағ жылдамдықпен таралады және Айдың қалпына байланысты кешігеді. Бұл кешігудің алатын уақыты тасқын жасын береді. Әрбір мұхитта фазалар бір мұхиттан екіншісіне қарай өзгеріп отыратын, Айдың әсерінен туындайтын тасқынның өзіндік жүйесі пайда болады.
2. Әдетте Ай Жердің экваторлық жазықтығында орналаспайды. (13.2 б сурет). Соның әсерінен аз жиілікті тасқында тәуліктік компонент пайда болады. Тасқынды қозғалыстың басқа да төмен жиілікті компоненттері де бар. Мысалы, Жер мен Айдың арасындағы максималды 4,06· 
метр қаышықтық апогейде 3,63· дейін, перигейде 27,55 күндік тәулік периодымен аутқиды. Сонымен қоса, Айдың қозғалу жазықтығы Жер – Күн жүйесінің тұтылу жазықтығына байланысты шамамен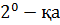 
аутқиды.
3. Көптеген әр түрлі мұхит бассейндерінің ерекшеліктеріне байланысты үлкен қиындықтар туындайды. Мысалы: континенттік шельфтердің жанында тасқын биіктігін мейілінше ұлғайтатын резонанстар пайда болуы мүмкін. §13.3 бөлімде резонанстардың тасқын энергетикалық қондырғыларын жасауда үлкен маңызы бар екендігі көрсетілген.
Ай тасқынының периодтылығы. Тасқынның жиілігін дұрыс дәлдікпен есептеу үшін тәулік мағынасында не жатқананын білуіміз керек (13.3 сурет). Жердегі А нүктесі Күннің екі рет осы нүктедегі меридианнан өтуі Күннің тәуліктік уақыт интервалы болып табылады. Негізінен бұл интервал тұрақты болып қалмайды,ол жыл көлемінде Жер орбитасының кедергісі әсерінен өзгеріп отырады,сол себепті таңдалған уақыт бойынша өлшем бірлік 
- 
интервал ретінде алынады.
Тура дәлдікте ол 24 сағ білдіреді,осыдан =86400c.
13.3 – сурет.Жерден бақыланатын әр түрлі үш " тәулік " салыстырмасы: жұлдызды және күндәк тәуліктер(а);жұлдызды және айлы тәуліктері(б).Күндік тәуліктер 24 сағатқа созылады,жұлдызды тәулік – одан ұзағырақ,айлы тәуліктер – одан қысқалау.Масштабтар қарастырылмаған.
Жұлдызды тәуліктер t* - осылайша есептелген "нақтыланған жұлдыздар",яғни қашықта орналасқан жұлдыздар,қатарының орташа интервалы Жерге қатысты шамалы аз.Жұлдызды тәуліктер дегеніміз – Жердің айналу периодын барынша дәл анықтайтын өлшем болып табылады13.3 суретте 
арасындағы айырмашылықтың Күн айналасындағы Жер(периоды 
=365,256 ) қозғалысымен қалай байланысты екендігі көрсетілген.Қандай да бір белгілі тәулік ортасында Жердің Е центрі,жер бетіндегі А нүктесі,S Күн және кейбір нақтыланған(фиксированная) жұлдыз бір сызық бойында жатыр делік.Күннің күндік тәуліктерінің өту мерзіміне байланысты А нүктесі мен Жердің центрі қайтадан бір сызыұ бойына келеді.Сол уақытта О нүктесі Күнге қатысты θ' бұрышпен Е' нүктесіне қарай жылжиды. - орташа күндік тәуліктің ұзақтығы болғандықтан,біз периодты сақтау мақсатында Жерді қатаң түрде орбита бойымен қозғалады деп ала аламыз.
Ол кезде мына теңдік сақталады
/2 
= / . (13.8)
Осы уақытта А нүктесі Е нүктесінің айналасынан (2 
) бұрышымен А'' қалпына қарай. 2 бұрышқа бұрылу уақыты t*,сондықтан:
θ'/2 = (
t*)/ t*. (13.9)
(13.8) бен (13.9) теңдіктерін теңестіре отырып аламыз:
t*= /[1+( / )] =86164с=23 сағ 56мин 4 с. (13.10)
Осылайша орташа күндік тәуліктердің ұзақтығы Жердің Е центрі, А нүктесі және Айдың М центрінің кезекті екі реттік бір нүкте бойына түсу аралығының орташа интервалы сияқты анықталады.13.3 б – суретте М нүктесінің Жер айналасындағы шеңберлі орбита бойымен қозғалу моменттері көрсетілген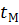 
уақыты кезінде Ай М нүктесінен 
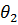бұрышпен М' нүктесіне ауысады, ал А нүктесі Жер қабатында 2 + 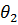бұрышпен А' нүктесіне қарай бұрылады.Осылайша
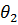/ 2 
/Т*=(
)/ t*. (13.11)
‾ Т*=27,32 тең болғандағы, қашықтағы бақылаушы тарапынан қарағандағы Жер айналасындағы Айдың айналу периоды.Бұл өлшем Жердің Кәнді айнала қозғалуына байланысты,Жер бетінде орналасқан бақылаушы нақтылаған ай(30күн) мәнінен сәл кем. 13.11- өрнек мынаны білдіреді:
= 
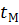[1 –(t*/ Т* 
]=89 428с=24сағ 50мин 28с. (13.12)
Күннің әсерінен туындайтын тасқындар.Аралас тасқындар. Нақтырақ айтқанда күндік тәуліктердің жартысына тең периодпен,күніне 2 рет болатын,Күн әсерінен туындайтын тасқындар Ньютонның теориясы арқылы түсіндіріледі.Күн тасқынының биіктігі Айдікімен салыстырғанда 2,2 есе кіші екендігі рас.Бұл,Жер бетіндегі нүктелердің d диаметрі бойынша қарама – қарсы Ай мен Күн тудыратын гравитациялық күштер айырмашылығының тасқын биіктігімен пропорционал екендігінен туындайды.Егер 
және 
- Күн мен Ай массасы,ал олардың Жерден ара қашықтығы – сәйкесінш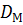е 
және 
болса,онда екі жүйе үшін де гравитациялық күштер пропорционалды М/ және күштер айырмашылығы
d = - 2Md/ 
. (13.13)
Күн мен Айдың 
және 
биіктіктерінің қатынасы сәйкес гравитациялық күштердің өсуіне пропорционалды:
= 
= 
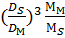= 2,2. (13.14)
Күн тасқындары Ай тасқындарымен бір немесе қарама-қарсы фазада туындауы мүмкін.Егер Күн,Жер және Ай бір сызықта болса – екі тасқын бір фазада болса: максималды биіктікті тасқын пайда болады. Бұл айына екі рет Айдың жаңада тууы мен толуы кезінде болады,ондай толқындар сизигиялық деп аталады.Күн – Жер және Жер – Күн бағыттары перпендикуляр(шаршы күйінде) болған кезде жалпы тасқын биіктігі минимал(шаршыланған тасқын) болады.Тасқындардың мұндай қайтулары да айына екі рет қайталанады.Егер тасқынның ұлғаю биіктігі - Күн және Ай тасқыны компоненттерінің жинақталуы болса,ал қйтуы – олардың шегерілуінің нәтижесі.Сизигиялық және шаршылынған тасқындардың қатынасын келесі түрде ұсынуға болады:
/ 
= (1 + 1 / 2,2)/(1 – 1 / 2,2) = 3. (13.15)
Практика жүзінде әр түрде динамикалық және жергілікті эффекттер шынайы тасқындардың осы қарапайымдатылған модельмен сәйкес келмеуін тудырады, / қатынасы әдетте 2-ге жақын мәнге ие болады.Сизигиялық тасқындар Айдың перигеясы кезінде оның апогеясы кезіне қарағанда үлкен биіктікке ие болады,ал жел екпінін қоса сансғандағы эффекттер комбинациясы ерекше жоғары тасулардың себепкері болуы мүмкін.
