3.1 Вариация массовых явлений. Значение средней величины
Вариацией значений какого-либо признака в совокупности называется различие его значений у разных единиц данной совокупности в один и тот же период или момент времени. Вариация признаков у единиц совокупности обусловлена различными условиями существования этих единиц.
Значение средних величин в их обобщающей функции, т.е в возможности замены множества различных индивидуальных значений единиц совокупности, некоторой средней величиной, характеризующей совокупность в целом. Средние величины позволяют обобщать информацию и сравнивать совокупности между собой. Средняя величина (Х) показывает типичный уровень исследуемого явления, приходящийся на единицу совокупности.
Основные виды средних величин:
1. Простая арифметическая средняя величина. Её расчет применяется, если признак у единиц совокупности распределен равномерно, т.е. каждое его значение встречается единожды или одинаковое количество раз (одинаковая частота (f) проявления признака: f1 = f2 = ………. = f n).
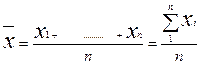 (3)
(3)
2. Взвешенная арифметическая средняя величина. Её расчет применяется, если признак у единиц совокупности распределен неравномерно, т.е. каждое его значение встречается неодинаковое количество раз (неодинаковая частота (f) проявления признака: (f1 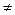 f2
f2 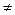 ……….
………. 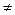 f n).
f n).
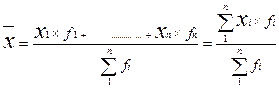 (4)
(4)
где Х1 – первое значение признака единиц совокупности, оно встречается f 1 раз (т.е у f 1 единиц совокупности наблюдается данное значение признака);
Х n - последнее значение признака единиц совокупности, оно встречается f n раз (т.е у f n единиц совокупности наблюдается данное значение признака);
n - общее количество единиц в совокупности, равняется общему количеству раз проявления признака в совокупности.
3.2 Виды рядов распределения
Ряд распределения называют также вариационным, ранжированным рядом. Его построение является первым этапом статистического изучения вариации.
Ряд распределения – это упорядоченное расположение единиц совокупности по возрастающему (убывающему) значению признака и подсчет единиц совокупности с тем или иным значением признака.
Виды рядов распределения:
Ряд распределения 1-го типа. В данном случае упорядоченно распределяются индивидуальные (дискретные или непрерывно-варьирующие) значения признака (Х i).
Ряд распределения 2-го типа. Если количество индивидуальных значений признака слишком велико, то вариационный ряд строится с помощью группировки. Образуют определенное количество групп с интервальным значением признака (Х j), расположенным также в порядке возрастания (чаще) или убывания. Пример такого ряда приведен в таблице 2 Приложения А
Для интервального ряда распределения расчет средневзвешенной величины признака корректируется с помощью следующей формулы


 (5)
(5)
 где Х/ j - серединное значение признака в каждом соответствующем интервале;
где Х/ j - серединное значение признака в каждом соответствующем интервале;
f j - частота соответствующего интервального признака;
k - количество интервалов (групп), на которое разделена совокупность.
3.3 Средние структурные характеристики вариационного ряда
Данные характеристики помогают оценить и количественно описать структуру изучаемой совокупности. Основными из них являются:
1. Мода распределения (Мо) – это варьирующее значение признака у единиц совокупности, встречающееся в вариационном ряду чаще всех остальных. Для первого типа ряда мода определяется без вычисления, по наибольшей частоте изучаемого признака. Для вариационного ряда второго типа (интервального), мода вычисляется по формуле 6. Модальный интервал определяется также по наибольшей частоте (f max) интервального признака.
 (6)
(6)
где Х о – начало модального интервала;
h – шаг (величина) модального интервала;
f 2 – частота модального интервала;
f 1 – частота интервала, предыдущего модальному;
f 3 – частота интервала, следующего за модальным.
Мода единственная структурная характеристика, которая рассчитывается на основании исходной информации об интервальном ряде распределения (X j, f j), все остальные структурные характеристики рассчитываются с помощью накопленной частоты S/.
Накопленная частота – это количество единиц совокупности со значением признака не больше максимального в каждом соответствующем интервале. В каждом последующем интервале S/ рассчитывается нарастающим итогом. В последнем интервале накопленная частота равняется общему количеству единиц в совокупности.
2. Медиана распределения (Ме) – это значение варьирующего признака у единицы совокупности, которая делит всю совокупность на две равные части.
Медиана рассчитывается по формуле 7. Все характеристики данной формулы (кроме S/ме-1) относятся к медианному интервалу.
 (7)
(7)
где S/ме-1 – накопленная частота интервала, предыдущего медианному
3. Квартили распределения (Q) – это величина варьирующего признака у единиц совокупности, которые делят всю совокупность на четыре равные части.
Квартили рассчитывается по формулам 8,9. Все характеристики данных формул (кроме S/Q1-1 и S/Q3- 1) относятся соответственно к первому квартильному и к третьему квартильному интервалам.
 (8)
(8)
где S/Q1-1 – накопленная частота интервала, предыдущему первому квартильному.
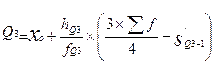 (9)
(9)
где S /Q3-1 - накопленная частота интервала, предыдущего третьему квартильному.
4. Децили распределения – это значения варьирующего признака у единиц совокупности, которые делят всю совокупность на десять равных частей.
Децили рассчитывается по формулам 10,11. Все характеристики данных формул (кроме S/D1-1 и S/D9-1) относятся соответственно к первому децильному и к девятому децильному интервалам.
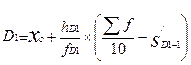 (10)
(10)
где S /D1-1 - накопленная частота интервала, предыдущего первому децильному.
 (11)
(11)
где S /D9-1 - накопленная частота интервала, предыдущего девятому децильному.






