| Вариант 1 1. Даны точки А(–6;3) и В(2;–7). Составить уравнение прямой, проходящей через точки А и В. Найти угловой коэффициент прямой, параллельной прямой АВ. Найти расстояние между точками А и В. 2. Определить угловой коэффициент k и отрезок b, отсекаемый на оси Oу для прямой 5х–у+3=0. 3. Дана гипербола х2–4у2=16. Найти: полуоси a и b; фокусы и эксцентриситет. 4. Найти центр и радиус окружности х2+у2–2х+4у–20=0. | Вариант 2 1. Даны точки А(–5;1) и В(4;–3). Составить уравнение прямой, проходящей через точки А и В. Найти угловой коэффициент прямой, параллельной прямой АВ. Найти расстояние между точками А и В. 2. Показать, что прямые 3 х–у+5=0 и х+3у–1=0 перпендикулярны. 3. Найти фокус F и уравнение директрисы параболы у2=24х. 4. Установить, что уравнение 5 х2+9у2–30х+18у+9=0. определяет эллипс. Найти координаты его центра, полуоси, эксцентриситет и уравнения директрис. |
| Вариант 3 1. Даны точки А(3;–4) и В(–6;8). Составить уравнение прямой, проходящей через точки А и В. Найти угловой коэффициент прямой, параллельной прямой АВ. Найти расстояние между точками А и В. 2. Даны вершины треугольника А(–2;2), В(3;4), С(–7;8). Найти уравнение медианы AD. 3. Дана гипербола 16х2–9у2=144. Найти полуоси a и b, фокусы, эксцентриситет. 4. Найти центр и радиус окружности х2+у2+4х–2у+5=0. | Вариант 4 1. Даны точки А(5;–2) и В(–7;4). Составить уравнение прямой, проходящей через точки А и В. Найти угловой коэффициент прямой, параллельной прямой АВ. Найти расстояние между точками А и В. 2. Составить уравнение прямой, проходящей через точки А(1;5), В(4;3). 3. Дана гипербола х2–4у2=16. Найти полуоси a и b; фокусы и эксцентриситет. 4. Установить, что уравнение 16х2+25у2+32х–100у–284=0 определяет эллипс. Найти координаты его центра, полуоси, эксцентриситет и уравнения директрис. |
| Вариант 5 1. Даны точки А(7;–1) и В(4;–5). Составить уравнение прямой, проходящей через точки А и В. Найти угловой коэффициент прямой, параллельной прямой АВ. Найти расстояние между точками А и В. 2. Составить уравнение прямой, отсекающей на оси ординат отрезок b=–5 и имеющей угловой коэффициент k=7 3. Дан эллипс 9 х2+25у2=225. Найти его полуоси, фокусы, эксцентриситет, уравнения директрис. 4. Установить, что уравнение 16х2–9у2–64х–54у–161=0 определяет гиперболу. Найти координаты ее центра, полуоси, эксцентриситет, уравнения асимптот и уравнения директрис. | Вариант 6 1. Даны точки А(1;7) и В(5;4). Составить уравнение прямой, проходящей через точки А и В. Найти угловой коэффициент прямой, параллельной прямой АВ. Найти расстояние между точками А и В. 2. Определить уравнение линии центров двух окружностей, заданных уравнениями (х+2)2+(у–1)2=16 и (х+2)2+(у+5)2=25. 3. Определить величину параметра и расположение ветвей параболы у2=6х относительно координатных осей. 4. Установить, что уравнение 4 х2+3у2–8х+12у–32=0 определяет эллипс. Найти координаты его центра, полуоси, эксцентриситет и уравнения директрис. |
| Вариант 7 1. Даны точки А(3;0) и В(4;–2). Составить уравнение прямой, проходящей через точки А и В. Найти угловой коэффициент прямой, параллельной прямой АВ. Найти расстояние между точками А и В. 2. Составить уравнение прямой, проходящей через точки А(1;5), В(4;3). 3. Определить величину параметра и расположение ветвей параболы у2=6х относительно координатных осей. 4. Найти центр и радиус окружности х2+у2+6х–4у+14=0. | Вариант 8 1. Даны точки А(–7;4) и В(5;–2). Составить уравнение прямой, проходящей через точки А и В. Найти угловой коэффициент прямой, параллельной прямой АВ. Найти расстояние между точками А и В. 2. Составить уравнение прямой, отсекающей на оси ординат отрезок b=–5 и имеющей угловой коэффициент k=7. 3. Дана гипербола х2–4у2=16. Найти: полуоси a и b; фокусы и эксцентриситет. 4. Найти центр и радиус окружности х2+у2+х=0. |
| Вариант 9 1. Даны точки А(5;–3) и В(0;4). Составить уравнение прямой, проходящей через точки А и В. Найти угловой коэффициент прямой, параллельной прямой АВ. Найти расстояние между точками А и В. 2. Показать, что прямые 3 х–у+5=0 и х+3у–1=0 перпендикулярны. 3. Дана гипербола 16х2–9у2=144. Найти полуоси a и b, фокусы, эксцентриситет. 4. Найти центр и радиус окружности х2+у2+у=0. | Вариант 10 1. Даны точки А(10;3) и В(–1;–3). Составить уравнение прямой, проходящей через точки А и В. Найти угловой коэффициент прямой, параллельной прямой АВ. Найти расстояние между точками А и В. 2. Определить уравнение линии центров двух окружностей, заданных уравнениями (х+2)2+(у–1)2=16 и (х+2)2+(у+5)2=25. 3. Дан эллипс 9 х2+25у2=225. Найти его полуоси, фокусы, эксцентриситет. 4. Установить, что уравнение 9х2–16у2+90х+32у–367=0 определяет гиперболу. Найти координаты ее центра, полуоси, эксцентриситет, уравнения асимптот и уравнения директрис. |
| Вариант 11 1. Даны точки А(–5;2) и В(4;–1). Составить уравнение прямой, проходящей через точки А и В. Найти угловой коэффициент прямой, параллельной прямой АВ. Найти расстояние между точками А и В. 2. Определить угловой коэффициент k и отрезок b, отсекаемый на оси Oу для прямой 5 х–у+3=0. 3. Найти фокус F и уравнение директрисы параболы у2=24х. 4. Установить, что уравнение 16х2–9у2–64х–18у+199=0 определяет гиперболу. Найти координаты ее центра, полуоси, эксцентриситет, уравнения асимптот и уравнения директрис. | Вариант 12 1. Даны точки А(3;–6) и В(–7;2). Составить уравнение прямой, проходящей через точки А и В. Найти угловой коэффициент прямой, параллельной прямой АВ. Найти расстояние между точками А и В. 2. Определить уравнение линии центров двух окружностей, заданных уравнениями (х+2)2+(у–1)2=16 и (х+2)2+(у+5)2=25. 3. Дана гипербола х2–-4у2=16. Найти полуоси a и b, фокусы и эксцентриситет. 4. Определить уравнение линии центров двух окружностей, заданных уравнениями (х–3)2+у2=9 и (х+2)2+(у–1)2=1. |
| Вариант 13 1. Даны точки А(1;–5) и В(–3;4). Составить уравнение прямой, проходящей через точки А и В. Найти угловой коэффициент прямой, параллельной прямой АВ. Найти расстояние между точками А и В. 2. Даны вершины треугольника А(–2;2), В(3;4), С(–7;8). Найти уравнение медианы AD. 3. Дан эллипс 9 х2+25у2=225. Найти его полуоси, фокусы, эксцентриситет. 4. Определить уравнение линии центров двух окружностей, заданных уравнениями х2+у2–4х+6у=0 и х2+у2–6х=0. | Вариант 14
1. Даны точки А(–4;3) и В(8;–6). Составить уравнение прямой, проходящей через точки А и В.
Найти угловой коэффициент прямой, параллельной прямой АВ.
Найти расстояние между точками А и В.
2. Составить уравнение прямой, отсекающей на оси ординат отрезок b=–5 и имеющей угловой коэффициент k=7.
3. Дана гипербола х2–4у2=16.
Найти полуоси a и b, фокусы и эксцентриситет.
4. Установить, что уравнение 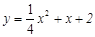 определяет параболу.
Найти координаты ее вершины и величину параметра. определяет параболу.
Найти координаты ее вершины и величину параметра.
|
| Вариант 15 1. Даны точки А(–5;2) и В(4;–7). Составить уравнение прямой, проходящей через точки А и В. Найти угловой коэффициент прямой, параллельной прямой АВ. Найти расстояние между точками А и В. 2. Определить угловой коэффициент k и отрезок b, отсекаемый на оси Oу для прямой 5х–у+3=0. 3. Дана гипербола 16 х2–9у2=144. Найти полуоси a и b, фокусы, эксцентриситет. 4. Определить полуоси эллипса 4 х2+9у2=25. | Вариант 16 1. Даны точки А(4;–7) и В(–2;5). Составить уравнение прямой, проходящей через точки А и В. Найти угловой коэффициент прямой, параллельной прямой АВ. Найти расстояние между точками А и В. 2. Определить уравнение линии центров двух окружностей, заданных уравнениями (х+2)2+(у–1)2=16 и (х+2)2+(у+5)2=25. 3. Найти фокус F и уравнение директрисы параболы у2=24х. 4. Установить, что уравнение у=46х2–8х+7=0 определяет параболу. Найти координаты ее вершины и величину параметра. |
Вариант 17
1. Даны точки А(–3;5) и В(4;0). Составить уравнение прямой, проходящей через точки А и В.
Найти угловой коэффициент прямой, параллельной прямой АВ.
Найти расстояние между точками А и В.
2. Составить уравнение прямой, отсекающей на оси ординат отрезок b=–5 и имеющей угловой коэффициент k=7.
3. Дана гипербола х2–4у2=16.
Найти: полуоси a и b, фокусы и эксцентриситет.
4. Установить, что уравнение 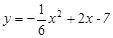 определяет параболу. Найти координаты ее вершины и величину параметра. определяет параболу. Найти координаты ее вершины и величину параметра.
| Вариант 18 1. Даны точки А(3;10) и В(–3;–1). Составить уравнение прямой, проходящей через точки А и В. Найти угловой коэффициент прямой, параллельной прямой АВ. Найти расстояние между точками А и В. 2. Определить угловой коэффициент k и отрезок b, отсекаемый на оси Oу для прямой 5х–у+3=0. 3. Определить величину параметра и расположение ветвей параболы у2=6х относительно координатных осей. 4. Определить полуоси эллипса 9х2+25у2=1. |
| Вариант 19 1. Даны точки А(2;–5) и В(–1;4). Составить уравнение прямой, проходящей через точки А и В. Найти угловой коэффициент прямой, параллельной прямой АВ. Найти расстояние между точками А и В. 2. Показать, что прямые 3 х–у+5=0 и х+3у–1=0 перпендикулярны. 3. Дана гипербола 16х2–9у2=144. Найти полуоси a и b, фокусы, эксцентриситет. 4. Определить полуоси эллипса х2+4у2=1. | Вариант 20 1. Даны точки А(–6;3) и В(2;–7). Составить уравнение прямой, проходящей через точки А и В. Найти угловой коэффициент прямой, параллельной прямой АВ. Найти расстояние между точками А и В. 2. Даны вершины треугольника А(–2;2), В(3;4), С(–7;8). Найти уравнение медианы AD. 3. Дана гипербола х2–4у2=16. Найти: полуоси a и b, фокусы и эксцентриситет. 4. Установить, что уравнение х=2у2–12у+14 определяет параболу. Найти координаты ее вершины и величину параметра. |
| Вариант 21 1. Даны точки А(5;1) и В(4;–3). Составить уравнение прямой, проходящей через точки А и В. Найти угловой коэффициент прямой, параллельной к прямой АВ. Найти расстояние между точками А и В. 2. Составить уравнение прямой, проходящей через точки А(1;5), В(4;3). 3. Определить величину параметра и расположение ветвей параболы у2=6х относительно координатных осей. 4. Определить полуоси эллипса 16х2+у2=16. | Вариант 22 1. Даны точки А(–7;4) и В(3;–2). Составить уравнение прямой, проходящей через точки А и В. Найти угловой коэффициент прямой, параллельной прямой АВ. Найти расстояние между точками А и В. 2. Определить угловой коэффициент k и отрезок b, отсекаемый на оси Oу для прямой 5 х–у+3=0. 3. Найти фокус F и уравнение директрисы параболы у2=24х. 4. Дан эллипс 9х2+5у2=45. Найти его полуоси, фокусы, эксцентриситет, уравнения директрис. |
Вариант 23
1. Даны точки А(8;–6) и В(–4;3). Составить уравнение прямой, проходящей через точки А и В.
Найти угловой коэффициент прямой, параллельной к прямой АВ.
Найти расстояние между точками А и В.
2 Даны вершины треугольника А(–2;2), В(3;4), С(–7;8).
Найти уравнение медианы AD.
3. Дана гипербола 16х2–9у2=144.
Найти полуоси a и b, фокусы, эксцентриситет.
4. Установить, что уравнение 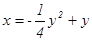 определяет параболу.
Найти координаты ее вершины и величину параметра. определяет параболу.
Найти координаты ее вершины и величину параметра.
| Вариант 24 1. Даны точки А(1;–3) и В(–5;4). Составить уравнение прямой, проходящей через точки А и В. Найти угловой коэффициент прямой, параллельной к прямой АВ. Найти расстояние меду точками А и В. 2. Составить уравнение прямой, проходящей через точки А(1;5), В(4;3). 3. Дана гипербола х2–4у2=16. Найти: полуоси a и b, фокусы и эксцентриситет. 4. Установить, что уравнение х=–у2+2у–1 определяет параболу. Найти координаты ее вершины и величину параметра. |
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Высшая математика в упражнениях и задачах: учеб. пособие / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова, С.П. Данко. – М.: Оникс, 2008. – 816 с.
2. Клетенник, Д.В. Сборник задач по аналитической геометрии / Д.В. Клетенник. – М.: Наука, Физматлит, 1998.
3. Кудрявцев, В.А. Краткий курс высшей математики: учеб. пособие / В.А. Кудрявцев, Б. П. Демидович. – М.: АСТ, 2008. – 654с.
4. Минорский, К.П. Сборник задач по высшей математике: учеб. пособие / К.П. Минорский. – 15-е изд. –М.: Физматлит, 2008. – 336 с.
5. Письменный, Д.Т. Конспект лекций по высшей математике (в 2 ч.) Ч.1 / Д.Т. Письменный. – 7-е изд. –М.: Айрис-пресс, 2007. – 288 с.
СОДЕРЖАНИЕ
ВВЕДЕНИЕ.. 3
Требования к оформлению контрольной работы.. 3
1. ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ НА ПЛОСКОСТИ.. 4
2. ПРЯМАЯ НА ПЛОСКОСТИ.. 4
Общее уравнение прямой. 4
Уравнение прямой с угловым коэффициентом.. 5
Уравнение прямой, проходящей через заданную точку М(х0;у0) в заданном направлении. 5
Уравнение прямой в отрезках. 5
Уравнение прямой, проходящей через две заданные точки М1(x1;y1) и М2(x2;y2) 5
Угол между двумя прямыми. 7
Условие параллельности прямых. 7
Условие перпендикулярности прямых. 7
3. КРИВЫЕ ВТОРОГО ПОРЯДКА.. 8
Окружность. 8
Эллипс. 9
Гипербола. 10
Парабола. 11
4. КОНТРОЛЬНЫЕ ЗАДАНИЯ.. 13
Вопросы для самопроверки. 13
Задания для самопроверки. 13
Задания для контрольной работы.. 16
БИБЛИОГРАФИЧЕСКИЙ СПИСОК.. 22






