Лекция 7. Действительные числа
7.1.Действительные числа. Расширенная числовая прямая. Окрестности
7.2.Модуль вещественного числа
7.3.Ограниченные и неограниченные множества. Конечные и бесконечные множества
7.4.Натуральные числа
7.5.Аксиома индукции и следствие из нее. Метод математической индукции
7.6.Принцип Архимеда. Усиленный принцип Архимеда
7.7. Лемма Бореля о покрытии
7.8. Теорема о вложенных промежутках
7.9. Открытые и замкнутые множества
Литература
А.В.Дорофеева «Высшая математика» Глава IV, § 4.1 – 4.4 стр.71-82
Дополнительно
Р.Курант, Г.Роббинс «Что такое математика?» Глава I «Натуральные числа» стр. 25-44, дополнение к главе I «Теория чисел» стр.45-76, глава II Математическая числовая система стр. 77-98
Контрольные задания
1.Как определяются элементы множества действительных чисел?
2.Дайте различные варианты определения модуля вещественного числа
3.Дайте определение инфинума (нижней грани) числового множества
4.Докажите, что ограниченное снизу числовое множество имеет нижнюю грань.
5.Как строится множество натуральных чисел?
6Докажите, что множество натуральных чисел не ограничено сверху
7.Методом математической индукции докажите
8.Сформулируйте определение ограниченного снизу множества и нижней границы, приведите примеры
9.Сформулируйте и докажите теорему Принцип Архимеда
10.Сформулируйте и докажите теорему Усиленный принцип Архимеда (включая доказательство второго случая для x<0).
Действительные числа. Расширенная числовая прямая. Модуль вещественного числа
Из элементарной математики известно, что действительные числа можно складывать, вычитать, умножать, делить и сравнивать по величине. Перечислим основные свойства, которыми обладают эти операции. Множество всех действительных чисел будем обозначать через R, а его подмножества называть числовыми множествами.
I. Операция сложения. Для любой пары действительных чисел а и b определено единственное число, называемое их суммой и обозначаемое а + b, так, что при этом выполняются следующие условия:
I.1. a + b = b + a, a,b 
R.
I.2. a + (b + с) = (a + b) + с, a,b,c R.
I.3. Существует такое число, называемое нулем и обозначаемое О,
что для любого a R выполняется условие а + 0 = а.
I.4. Для любого числа a R существует число, называемое ему
противоположным и обозначаемое -а, для которого а + (-а) = 0.
Число а + (—b), а, b R, называется разностью чисел а и b и обозначается а — b.
П. Операция умножения. Для любой пары действительных чисел а и b определено единственное число, называемое их произведением и обозначаемое ab (a • b), такое, что выполняются следующие условия:
II.1. ab = ba, a, b R.
II.2. а(bс) = (ab)c, a,b, R
II.3. Существует такое число, называемое единицей и обозначаемое 1, что для любого а е R выполняется условие а • 1 = а.
II.4. Для любого числа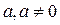 
существует число, называемое ему обратным и обозначаемое a -1 или 
, для которого 
= 1.
Число а 
, называется частным от деления а на b и обозначается а: b или 
или а/b.
III. Связь операций сложения и умножения:
для любых a,b,c R выполняется условие (а + b)с = ac+bc
IV. Упорядоченность. Для действительных чисел определено отношение порядка. Оно состоит в следующем. Для любых двух различных чисел а и b имеет место одно из двух
соотношений: либо а < b (читается "а меньше b"), или, что то же самое, b > а (читается "b больше а"), либо а > b, или, что то же самое, b < а. При этом предполагается, что выполняются следующие условия:
IV1. Транзитивность. Если а<b и b < с, то а < с.
IV2- Если а < b, то для любого числа с имеет место а + с < b + с.
IV3. Если а > b и с > 0, то ас> bc.
Соотношения порядка называют также сравнением действительных чисел по величине или неравенствами. Запись а ≤ b, равносильная записи b ≥ а, означает, что либо а < b, либо а = b.
Из выполнения условий IV2 и IV3 вытекает одно важное свойство, называемое плотностью действительных чисел: для любых двух различных действительных чисел а и b, например, таких, что а < b, существует такое число с, что а < с < b. В самом деле, сложив каждое из равенств a = a, b = b c неравенством а < b, получим 2a<a + b<2b,
откуда а < 
< b, т. е. в качестве числа с можно взять .
Множество действительных чисел обладает еще свойством непрерывности.
V. Непрерывность. Для любых непустых числовых множеств X и Y таких, что для каждой пары чисел х 
X и у Y выполняется неравенство x≤y, существует число а, удовлетворяющее условию x≤a≤y, х X и у Y (см рис.7.1.)
Рис. 7.1.
Перечисленные свойства полностью определяют множество действительных чисел в том смысле, что из этих свойств следуют и все остальные его свойства. Поэтому можно дать аксиоматическое определение множества действительных чисел следующим образом.
Определение 7.1.
Множество элементов, обладающих свойствами I-V, содержащее более одного элемента, называется множеством действительных чисел, а каждый его элемент — действительным числом.
Это определение однозначно задает множество действительных чисел с точностью до конкретной природы его элементов. Оговорка о том, что в множестве содержится более одного элемента, необходима потому, что множество, состоящее из одного только нуля, очевидным образом удовлетворяет условиям I-V.
Геометрически множество действительных чисел изображается направленной (ориентированной) прямой, а отдельные числа — точками этой прямой (см.рис. 7.1.(2))
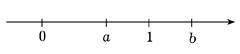
Рис. 7.1. (2)
Поэтому совокупность действительных чисел часто называют числовой прямой или числовой осью, а отдельные числа — ее точками. В связи с этим иногда вместо а < b (соответственно вместо b > а) говорят, что точка а лежит левее точки b (точка b лежит правее точки а).
Часто бывает удобно дополнить множество действительных чисел элементами, обозначаемыми через +∞ и — ∞ и называемыми соответственно плюс бесконечностью и минус бесконечностью, считая при этом по определению, что для любого числа х R. выполняется неравенство -∞< х < +∞.
Множество действительных чисел R, дополненное элементами +∞ и —∞, называется расширенным множеством действительных чисел (расширенной числовой прямой) и обозначается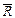 
Иногда бывает удобно дополнить множество действительных чисел R одним элементом ∞ (бесконечностью без знака), в этом случае бесконечность ∞ уже не связана соотношением порядка с действительными числами. Бесконечности +∞, ∞и ∞ называются также бесконечно удаленными точками числовой прямой, в отличие от ее остальных точек, которые называются конечными точками числовой прямой.
Сформулируем определения некоторых важных типов подмножеств расширенной числовой прямой R. Пусть a 
, b , а ≤b. Множество
[а, b] = {х: х , а ≤x≤b}
называется отрезком, множество
(a,b) = {х: х , а < х < b}
— интервалом, множества
[а, b) = {х: х , а ≤ х < b},
(а,b] = {х: х , а < х ≤b}
— полуинтервалами, а все они — промежутками расширенной числовой оси. Точки а и b называются концами этих промежутков, а точки х такие, что а < х < b, — их внутренними точками. Если а и b — числа, а ≤b, то число b — а называется длиной соответствующего промежутка, а сам промежуток называется конечным.
Определение 7.1(2).
U(a, ε) = (a - ε, a + ε) (см рис.7.1(3)
Рис. 7.1(3).
