Примером колебательного звена является электрический колебательный контур, груз на пружине, маятник, стрелочный прибор.
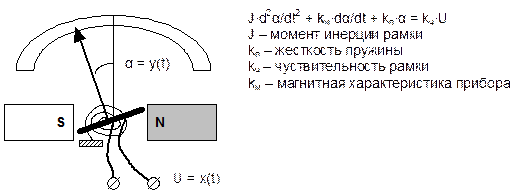
Переходная характеристика.
Переходная характеристика колебательного звена имеет вид:
h(t) = L-1[W(s)/s)] = L-1[K/[s·(T2s2 + 2T ξs +1)]] =
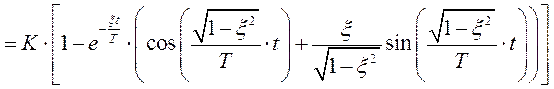
Переходная функция имеет достаточно сложный вид, но наиболее характерно то, что имеется экспоненциальное затухание переходного процесса с коэффициентом - ξ/T,атакже колебательность с частотой 
.
Здесь важно отметить, что частота зависит от коэффициента затухания. При ξ → 0 ωк → 1/T; при ξ → 1 ωк → 0.
Весовая функция.
Весовая функция колебательного звена имеет вид:
w(t) = L-1[W(s)] = L-1[K/(T2s2 + 2T ξ s +1)] =
Рис. 4.4. Переходная и весовая характеристики колебательного звена.
Частотные характеристики.
Частотные характеристики колебательного звена имеют следующий вид:
W(jω) = K/(T2·(–jω)2 + 2T ξ ·jω + 1) =
Переход к асимптотической ЛАХ: заменяем истинную ЛАХ – ломаной асимптотической. Выделим области низких и высоких частот и по отдельности рассмотрим поведение ЛАХ в этих областях.
Область низких частот: Tw << 1; т.е. w << 1/T; можно пренебречь выражением T2w2. Получаем: L(w) = 20lgK. Это горизонтальная прямая.
Область высоких частот: Tw >> 1; т.е. w >> 1/T; можно пренебречь 1 в сравнении с выражением T2w2. Получаем L(w) = 20lgK – 40lg(Tw). Это – уравнение прямой с наклоном -40дб/декаду.
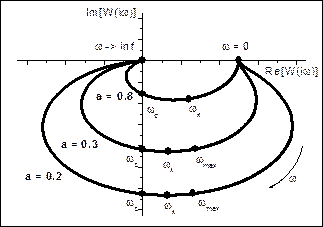
Рис. 4.5. АФЧХ, ЛАХ и ЛФХ колебательного звена.
Точке пересечения этих прямых соответствует сопрягающая частота ω1 = 1/T.
Принципиальное отличие ЛАХ колебательного звена от ЛАХ инерционных звеньев состоит в том, что в районе сопрягающей частоты ωс = 1/T имеется максимум (так называемый "горб"), из-за чего поведение асимптотической ЛАХ в этой области может существенно отличаться от истинной. Это явление называется резонансом. При этом максимум усиления амплитуды достигается при частоте:
, а 
.
Как видно из приведенного выражения, резонанс в колебательном звене может возникнуть только при малых значениях a (
), т.е. когда рассеяние энергии во внешнюю среду невелико.
Также надо отметить, что сопрягающая частота (ωс), частота собственных колебаний (ωк) и резонансная частота (ωmax) колебательного звена не совпадают. Однако при малых значениях параметра ξ, когда явление резонанса проявляется достаточно сильно, разница между ωс, ωк и ωmax мала, и на практике эти частоты обычно считают равными ω* = 1/T.
Интегрирующее звено
Передаточная функция.
Передаточная функция интегрирующего звена имеет вид:
W(s) = K/s = 1/T·s, где K – коэффициент усиления; T – постоянная времени (время интегрирования); T = 1/K.
