Методические указания к выполнению контрольной работы

3.1 Раздел «Теоретическая механика»

В задачах статики приходится рассматривать равновесие несвобод­ных тел, лишенных возможности перемещаться в направлении действия приложенных к ним так называемых активных сил. Тела, ограничиваю­щие движение рассматриваемого тела, называются связями. Между телом и связью на основании закона равенства действия и противодействия возникают равные и противоположно направленные силы взаимо­действия.

Сила, с которой связь действует на рассматриваемое тело, назы­вается реакцией связи или просто реакцией.

Сила, с которой тело действует на связь, называется силой давле­ния на связь. Таким образом, сила реакции и сила давления на связь – две равные по модулю силы, имеющие противоположное направление.

Задачи на равновесие несвободных тел решаются втакой после­довательности:

1. Выяснить, какое тело (точка) в данной задаче находится всостоянии равновесия, и приложить к нему заданные силы.

2. Выделенное тело освободить от связей и их действие заменить силами реакций.

3. Выбрать направление координатных осей.

4. Составить уравнения равновесия в одном из двух видов: Σ x_i = 0; ΣМ_A=0; ΣМ_В= 0; либо ΣХ_i= 0; ΣY_i=0; ΣМ_В = 0.

5. Решить уравнения равновесия.

6. Проверить правильность решения задачи.

Методику решения задач с помощью уравнений равновесия рассмот­рим на примерах.

Для решения первой задачи (№ 1-20), которая относится к теме 1.2 «Плоская система произвольно расположенных сил», требуется составить уравнения проекций на координатные оси и уравнения моментов.

Проекция вектора – скалярная величина, которая определяется отрезками, отсекаемыми перпендикулярами, опущенными из начала и конца вектора на ось. Проекция вектора считается положительной (+), если направление ее совпадает с положительным направлением оси (рис. 1, а), и отрицательной (—) если проекция направлена в противо­положную сторону (рис. 1,б).

 

 

 

Рис. 1

 

Моментом силы относительно точки называется произведение модуля силы на плечо, т. е. на длину перпендикуляра, восставленного из точки, относительно которой берется момент, к линии действия силы. Момент принято считать положительным, если он стремится повернуть тело по часовой стрелке (рис. 2, а), и отрицательным (рис. 2, б), если вращение направлено в противоположную сторону.

 

 

Рис. 2

 

Между моментом пары и моментами сил пары относительно любой точки существует такая важная зависимость: алгебраическая сумма моментов сил пары относительно любой точки — величина постоянная для данной пары и равна ее моменту. Так как пара сил не имеет равно­действующей, ее нельзя уравновесить одной силой.

Момент пары сил в СИ выражается в ньютонометрах (Н·м) или в единицах, кратных ньютонометру: кН·м, МН·м и т. д.

Пример 1. Однородная балка закреплена в точке А с помощью шарнирно-неподвижной опоры и поддерживается в точке В стержнем (рис. 3, а). Найти реакции шарнирно-неподвижной опоры и стержня ВС. Силой тяжести балки и стержня пренебречь.

Рис. 3

При рассмотрении пространственной системы сил необходимо ввести понятие о моменте силы относительно оси.

Моментом силы относительно оси называется алгебраическая (скалярная) величина, равная моменту проекции силы на плоскость, перпендикулярную оси относительно точки пересечения оси с плос­костью.

Последовательность определения момента силы F относительно оси z (рис. 2, в): а) задают модуль и направление силы F; б) указывают координатные оси; в) перпендикулярно оси выбирают плоскость XOY; г) силу F проецируют на эту плос­кость и определяют модуль F_xy этой про­екции; д) опустив перпендикуляр из на­чала координат на проекцию F_xy, опре­деляют плечо а = О К; е) определяют момент M₂(F) = F_xya.

Момент силы относительно оси ра­вен нулю, если сила и ось лежат в
одной плоскости: а) сила действует вдоль оси; б) сила F пересекает
ось z; в) сила F параллельна оси z.

Решение. Изобразим балку вместе с нагрузками, соблюдая заданные размеры ее участков и угла а (рис. 3, б).

Освободим балку от связей в точках А и В, заменив эти связи их реакциями. Начало координат поместим в точке А, ось х совместим с осью балки, а ось у направим перпендикулярно балке. Если стержень растягивается, то его реакция направлена в сторону от рассматриваемого тела, а при сжатии – от стержня к телу.

Составим три уравнения равновесия:

Σ X_i = 0 – алгебраическая сумма проекций сил на ось х;

Σ Y_i = 0 – алгебраическая сумма проекций сил на ось у;

Σ М_А = 0 – алгебраическая сумма моментов относительно точки А.

Уравнение проекций сил на ось х имеет вид

Силы F и Y_A не вошли в уравнение, так как они перпендикулярны оси х и их проекции на эту ось равны нулю. Проекции силы на ось у

реакция Х_А перпендикулярна оси у и ее проекция на эту ось равна нулю. Для составления уравнения моментов за центр моментов принимаем точку А. Плечо силы R_B равно длине перпендикуляра, восставленного из точки А (центра моментов) к линии действия силы R_B. Из рис. 3, б видно, что AD = (а + b)cos60°.

Подставив числовые значения, получим

Выразим из (2)

Подставив значения сил, получим

 

Из (1)

Проверим правильность решения задачи, составив уравнения моментов относительно точки В:

Подставим числовые значения 3000 • 4 – 2000 – 4000 • 2,5 = 0; 12000 – 12000 = 0.

Задача решена верно, так как при подстановке получили тож­дество 0 = 0.

Вторую задачу контрольной работы (№ 21-30) можно решать после изучения тем 1.3 «Пара сил» и 1.4 «Плоская система произвольно расположенных сил».

Напомним, что в шарнирно-подвижной опоре А реакция направ­лена по нормали к опорной поверхности (рис. 4, б). Модуль и направ­ление реакции шарнирно-неподвижной опоры В неизвестны. В этом слу­чае реакцию R_B заменяют двумя составляющими: вертикальной Y_B и горизонтальной Х_в. Освобожденная от связей балка изображена на рис. 4, б. Порядок решения подобных задач такой же, как в при­мере 1.

Рис. 4

 

Пример 2. Для балки (рис. 5, а)определить опорные реакции по следующим данным: а =1,5 м, b = 1 м, с = 2 м, F₁ = 8 кН, F₂ = 10 кН, q = 0,4 кН/м, М = 5 кН·м.

Рис. 5

 

Решение. Освободим балку от связей, отбросив опоры и прило­жив вместо них неизвестные реакции (рис. 5, б). Напомним, что для плоской системы параллельных сил достаточно двух уравнений равно­весия:

Уравнения моментов относительно точки А:

Уравнение моментов относительно точки В:

Из первого уравнения

Из второго уравнения

Значение реакции R_B получено со знаком минус. Это означает, что она направлена вертикально вниз.

Для проверки правильности найденных реакций опор балки со­ставляем уравнение ΣY=0; R_A – F ₁ – qc+F₂+R_B = 0, или 4,8 – 8 – 2·0,4+10 – 6 = 14,8 – 14,8 = 0.

Следовательно, R_A и R_B определены верно.

Третью задачу контрольной работы (31-40) решать после изучения темы 1.6 «Центр тяжести». В этих задачах требуется находить центр тяжести плоских фигур, составленных из простых геометрических фигур. Положение центра тяжести плоской фигуры определяется по формулам:

где х_с и y_с – искомые координаты центра тяжести фигуры; x_i и y_i – координаты центров тяжести составных частей фигуры, которые опре­деляются из заданных размеров; А_i – площади составных частей.

Последовательность решения таких задач рассмотрена в примере.

Пример 3. Вычислить координаты центра тяжести сечения плоской фигуры (рис. 6, а).

Рис. 6

Решение. Заданную плоскую фигуру разбиваем на составные части, центры тяжести которых легко определяются (рис. 6, б)– прямоугольник I, треугольник II и прямоугольники III и IV.

Располагаем координатные оси, как показано на рис. 6, а.

Находим площади каждой части и координаты х_с и у_с их центров тяжести С_i. Все эти данные заносим в табл. 2.

Вычисляем координаты х_с и у_с центра тяжести плоской фигуры:

 

Таблица 2

Составная часть	Площадь составной части Ai, мм2	Координаты центров тяжести каждой части
xi, мм	yi, мм
I	300·160 = 48000 = 48·103
II	1/2·120·180=10800= = 10,8·103
III	120·120=14400=14,4·103
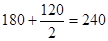
IV	80·60= 4800= 4,8·103

 

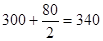
При решении задач можно использовать метод отрицательных площадей, как это показано на рис. 6, в. Здесь данная фигура разделе­на на три части: прямоугольники I и III и треугольник II, причем площадь треугольника II, вырезанная из плоской фигуры, берется со знаком минус, т. е. считается отрицательной. Легко проверить, что если при таком разделении фигуры все исходные данные свести в табл. 3 и выполнить вычисления, то получится тот же результат.

 

Таблица 3

Сос­тав­ная часть	Площадь составной части Ai, мм2	Координаты центра тяжести каждой части
xi, мм	yi, мм
I	300·280=84000=84·103
II	=10,8·103
III	60·80=4800=4,8·103

 

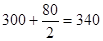
Определяем

Центр тяжести тела в обоих случаях совпадает, что указывает на правильность решения задачи.

Четвертую задачу контрольной работы (№ 31-40) следует решать после изучения тем 1.7 «Основные понятия кинематики» и 1.8 «Кине­матика точки». В задачах рассматривается равнопеременное движение точки. Следует учесть, что при использовании уравнения равно­переменного движения точки s = v₀t + (a,t²/2)по криволинейной траек­тории кроме касательного ускорения у точки возникает нормальное ускорение а_п = v²/p, направленное по радиусу кривизны траектории к ее центру.

Для решения задач используются соответствующие готовые урав­нения и формулы, выведенные в учебниках (см. приложение, табл. П. 1).

Решение задач целесообразно иллюстрировать рисунками.

Пример 4. По дуге радиусом r = 1200 м (рис. 7) движется поезд, его скорость в. начале движения по дуге составляет v_o = 60 км/ч.

Рис. 7

 

После того как поезд прошел расстояние 800 м, его скорость умень­шилась до 36 км/ч. Определить полное ускорение в начале и конце движения.

Из первого уравнения

Решение. Определим касательное ускорение из уравнений:

Из второго уравнения

Так как движение равномерно за­медленное, то касательное ускорение в течение всего времени движется пос­тоянно.

Найдем нормальное ускорение:

в начале движения а_n = 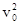/ r = 16,7²/1200= 0,23 м/с²;

в конце движения а_n = v²/r = 10²/ 1200 = 0,08 м/с²;

полное ускорение:

в начале движения м/с²;

в конце движения м/с².

Пример 5. Точка движется прямолинейно по закону s=t⁴+2t (s – в метрах, t – в секундах). Найти ее среднее ускорение в проме­жутке между моментами t_i = 2 с и t₂ = 4 с, а также истинное ускорение в момент t₃ = 3 с.

Решение. Сначала определим скорость точки

Подставив вместо t его значения t₁ = 2 с и t₂ = 4 с, находим

Следовательно, приращение скорости за данный промежуток времени

 

Среднее ускорение точки

Для определения ускорения точки в любой момент времени возьмем производную от скорости по времени

и подставим в это уравнение вместо t его значение t₃ = 3 с:

Пятую задачу контрольной работы (№ 41-50) следует решать после изучения тем 1.9 «Простейшие движения твердого тела», 1.12 «Основные понятия и аксиомы динамики», 1.13 «Метод кинетостатики для материальной точки». Шестую задачу контрольной работы (№ 51-60) следует решать после изучения тем 1.14 «Работа и мощность», 1.15 «Теоремы динамики». Рассматривая вращательное движение твер­дого тела, необходимо отчетливо уяснить, что вращение тела харак­теризуется угловыми величинами (угол поворота φ, угловая скорость ώ и угловое ускорение ε), а отдельные точки вращающегося тела совер­шают криволинейное движение (по окружностям) и их движение характеризуется линейными величинами (путь s, скорость v и ускорение a_τ, a_n).

При решении задач динамики необходимо пользоваться принципом Даламбера, с помощью которого задачи динамики решаются с исполь­зованием уравнения равновесия статики. Согласно принципу Даламбе­ра, в каждый данный момент действующие на материальную точку силы уравновешиваются силами инерции.

При решении задач рекомендуется такая последовательность: 1) выделить точку, движение которой рассматривается в данной задаче; 2) выяснить, какие активные силы действуют на точку и изобразить их на рисунке; 3) освободить точку от связей, заменив их реакциями; 4) к образовавшейся системе сил добавить силу инерции, помня, что направлена она по линии вектора ускорения точки, но в противоположную сторону; 5) выбрать расположение осей координат и составить два уравнения проекций всех сил на эти оси (ΣX_i = 0; ΣY_i = 0); 6) решив уравнения, определить искомые значения величин.

Пример 6. Маховик диаметром 0,8 м начинает вращаться из сос­тояния покоя. Через 10 с после начала движения скорость точек обода маховика достигает 8 м/с. Определить ускорение этих точек. Чему равно число оборотов маховика за первые 10 с равнопеременного вращения?

Решение. По значению скорости точки находим угловую скорость вращения маховика через 10 с после начала вращения:

Угол поворота маховика за 10 с

 

 

Число оборотов маховика за 10 с

Угловое ускорение маховика

Нормальное ускорение точек обода маховика в момент t = 10

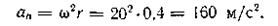
Касательное ускорение точек обода маховика

а_τ = εr = 2·0,4 = 0,8 м/с².

Пример 7. Груз массой 200 кг (рис. 8) опуска­ется равноускоренно с помощью невесомого троса, перекинутого через блок, и в первые 5 с прохо­дит 10 м. Определить силу натяжения троса.

Рис. 8

 

Решение. Обозначив груз точкой А, при­ложим к нему силу тяжести G, реакцию троса Т и добавим к ним силу инерции F_и направив ее в сторону, противоположную ускорению.

Ускорение а определяем из уравнения рав­нопеременного движения s = at²/2, так как начальная скорость v₀ = 0:

Согласно принципу Даламбера, силы G, Т и F_и находятся в рав­новесии, т.е. Т +F_и – G = 0, откуда Т= G – F_и. Выражая силу инер­ции и силу тяжести через массу груза (F_и = ma, G = mg), получаем T = mg – ma = m(g – a) = 200(9,81 – 0,8) = 1802 H.

Пример 8. Для остановки поезда, движущегося по прямолинейному участку пути со скоростью v = 10 м/с, производится торможение. Через сколько секунд остановится поезд, если при торможении разви­вается постоянная сила сопротивления, равная 0,02 силы тяжести поезда? Какой путь пройдет поезд до остановки?

Решение. Поезд совершает поступательное движение. Рассмат­ривая его как материальную точку М (рис. 9), движущуюся в направ­лении оси Ох, укажем действующие силы: G – сила тяжести поезда, R – нормальная реакция рельсов, F – сила сопротивления, направлен­ная противоположно вектору скорости. Силы G и R уравновешиваются согласно аксиоме действия и противодействия.

Рис. 9

По теореме об изменении количества движения материальной точки в проекции на ось Ох

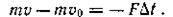
Так как F = 0,02G = 0,02mg, t_o = 0, v_o = 10 м/с, v = 0, получим – mv_o = – 0,02mg Δ t.

Откуда

Для определения пройден­ного пути поездом до его ос­тановки воспользуемся теоремой об изменении кинетической энер­гии:

Работа силы торможения отрицательна ( а = = 180° и cosa = – 1), поэтому

и путь, пройденный поездом:

 

3.2 Раздел «Сопротивление материалов»

Приступить к решению задач раздела «Сопротивление материалов» следует после изучения основных вопросов программы предмета и повторения темы «Статика» (методика определения реакций связей балок и стержневых конструкций). В процессе изучения учебного материала требуется внимательно разобрать соответствующие примеры решения задач, которые имеются в учебниках и пособиях. Затем самостоятель­но решить несколько аналогичных задач и только после этого выпол­нить контрольное задание.

Изучая соответствующий учебный материал, следует иметь четкое представление о методе сечений для определения внутренних силовых факторов (ВСФ). Легко запомнить все пункты метода сечений, если записать их словом «РОЗУ»:

Р – разрезаем тело плоскостью на две части,

О – отбрасываем одну часть,

З – заменяем действие отброшен­ной части внутренними силами,

У – уравновешиваем оставшуюся часть и из уравнения равновесия определяем внутренние силы.

В общем случае нагружения тела внутренние силы (силы упругости), возникающие в поперечном сечении нагруженного бруса, могут быть заме­нены их статическим эквивалентом — главным вектором и главным моментом. Если последние разложить по осям координат (рис. 13), то получим шесть составляющих с общим названием «внутренне силовые факторы»: N_z – продольная сила; Q_x, Q_y – поперечные силы; М₂ – крутящий момент; М_х и М_у – изгибающие моменты.

Рис. 13

 

Числовая мера интенсивности внутренних сил, приходящихся на единицу площади сечения у какой-либо точки, называется напряже­нием.

Шесть внутренних силовых факторов вместе с известными внеш­ними силами на оставшейся части бруса образуют уравновешенную систему сил, для которой можно составить шесть уравнений равновесия. В каждое из этих уравнений входит один из неизвестных внутренних силовых факторов. Решая уравнение, найдем:

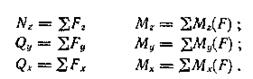
Нормальное напряжение а – следствие возникновения продоль­ной силы N_z илиизгибающих моментов М_х и М_у; касательные на­пряжения τ – следствие возникновения поперечных сил Q_x и Q_y или крутящего момента M_z.

Числовое значение напряжений в поперечных сечениях тела зави­сит не только от возникновения силового фактора, но и от размеров поперечного сечения – от соответствующей геометрической характе­ристики прочности сечения.

Условием прочности при расчете по допускаемому напряжению называется неравенство вида σ≤[σ] или τ≤[τ], где [ σ ]и [τ] - до­пускаемые напряжения, т. е. максимальные значения напряжений, при которых гарантируется прочность детали.

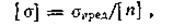
гдеσ_пред – предельное напряжение для материала рассчитываемой детали; [n] – коэффициент запаса прочности детали, зависит от ответственности детали, срока службы, точности расчета и других факторов.

При решении задач следует применять единицы Международной системы (СИ), а также кратные и дольные от них.

Единицей давления, механического напряжения и модуля упру­гости установлен паскаль (1 Па = 1 Н/м²) и кратная единица – мегапаскаль (1 МПа = 10⁶ Па). Отметим, что 1 МН/м² = 1 Н/мм².

К решению первой задачивторой контрольной работы (№ 61-70) следует приступать после изучения темы «Растяжение и сжатие», метода сечений и разбора решенных примеров в данном пособии и рекомендуемой литературе.

Задача требует от учащегося умения определить продольные си­лы, нормальные напряжения, удлинения и построить эпюры N и σ.

Растяжением (сжатием) называют такое нагружение бруса, при котором в поперечных сечениях возникает только один внутренний силовой фактор – продольная сила N, влюбом поперечном сечении бруса численно равная алгебраической сумме внешних сил, действую­щих на оставленную часть бруса.

Простейшие случаи растяжения и сжатия представлены на рис. 14, а, б; в центрах тяжести торцевых поперечных сечений бруса приложены две равные противоположно направленные силы, линии, дей­ствия которых совпадают с осью бруса.

Рис. 14

 

Продольные силы N, соответствующие деформации растяжения, считаются положительными (рис. 14, в), в противном случае они отри­цательные (рис. 14, г).

Удлинение (укорочение) бруса или отдельных его участков опре­деляется по формуле Гука

которую можно представить еще в виде Δ l = σ (1/Е), помня, что N/A = σ.

Пример 9. Для двухступенчатого бруса (рис. 15, а) определить и построить эпюры продольных сил и нормальных напряжений. Опреде­лить удлинение (укорочение) бруса. Модуль упругости Е = 2·10⁵ Н/мм².

Рис. 15

 

Решение. Разделим брус на участки, границы которых опре­деляются сечениями, где изменяется площадь поперечного сечения или приложены внешние нагрузки. При составлении уравнений равновесия надо использовать правила знаков проекций сил, принятых в теорети­ческой механике, а именно: проекция силы берется со знаком плюс, если ее направление совпадает с положительным направлением оси. Мысленно рассечем брус в пределах первого участка и отбросим верхнюю часть бруса (рис. 15, б). Вместо отброшенной верхней части приложим внутреннюю силу N₁, которая уравновешивается силой F₁:

Аналогично, в пределах участка II (рис. 15, в) отбросим верхнюю часть бруса и рассмотрим оставленную часть бруса с действующей силой F₁, которая уравновешивается продольной силой N_II:

Продольная сила на участке III (рис. 15, г) уравновешивается в сечении внешними силами F₁ и F₂ и равна их алгебраической сумме:

В пределах каждого участка нагружения продольная сила по­стоянна, а потому на эпюре изобразится линией, параллельной оси бруса. Эпюра штрихуется линиями, перпендикулярными оси бруса.

Построим эпюру N (рис. 15, д). Для этого параллельно оси бруса проведем базовую (нулевую) линию. Левее ее откладываем значение продольной силы, вызванной сжатием участка, а правее – растяжением. В пределах участка III брус сжат (N_III= – 10 кН), в пределах участков II и I брус растянут (N_II = N_I –40 кН).

Для определения напряжений а в поперечных сечениях значение продольных сил необходимо разделить на площади соответствующих сечений

Площадь поперечного сечения бруса первого участка

Площадь поперечного сечения бруса на участках II и III

Находим напряжения на отдельных участках бруса и строим эпюру (рис. 15, е):

В соответствии с полученными значениями напряжений строим эпюру нормальных напряжений.

При построении эпюр продольных сил и нормальных напряжений нет необходимости изображать отдельно отсеченные части бруса, доста­точно обратить внимание на то, что продольная сила, возникающая в произвольном сечении, равна алгебраической сумме всех внешних сил, приложенных к брусу по одну сторону от рассматриваемого сечения, а нормальное напряжение равно отношению продольной силы к соответствующей площади поперечного сечения. Кроме того, при по­строении эпюр и проверке их правильности следует руководствоваться следующими правилами:

1. Скачки на эпюрах N имеют место в точках приложения сосредоточенных сил. Величина скачка равна внешней силе.

2. На эпюре а скачки имеют место не только в точках приложе­ния сосредоточенных сил, но и в местах изменения площади поперечно­го сечения.

3. Знаки на участках эпюры а должны совпадать со знаками на соответствующих участках эпюры N.

Полное удлинение бруса можно найти, воспользовавшись эпюрой N, представленной на рис. 15, д, т. е. полное удлинение бруса равно алгебраической сумме удлинений его участков:

или

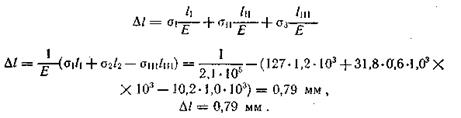
Во второй задаче (№ 71-80) рассматриваются статически неоп­ределимые системы с числом неизвестных реакций связей, на единицу превышающем число уравнений статики (уравнений равновесия), кото­рые можно составить для этой системы. Поэтому при решении подоб­ных задач рекомендуется придерживаться такой последовательности:

1) брус, равновесие которого рассматривается, освободить от связей и заменить действие связей реакциями;

2) составить уравнение равновесия, в него войдут неизвестные реакции связей, без которых невозможно определить продольные силы, возникшие в стержне (уравнение проекций всех внешних сил на ось и уравнение моментов относительно неподвижного шарнира, которым жесткий брус прикреплен к стене);

3) рассмотреть картину деформации системы, изобразив ее на рисунке;

4) рассматривая с геометрической точки зрения картину дефор­мации, составить уравнение перемещений, в которое войдут те же не­известные реакции, что и в уравнении статики;

5) произвести в уравнении перемещений необходимые упрощения;

6) уравнение статики и уравнение перемещений решить совместно, определить искомые реакции связей;

7) определить внутренние силовые факторы (продольные силы) в частях деформируемого стержня (если в задаче требуется определить допускаемую нагрузку), выразить продольные силы через искомую нагрузку;

8) завершить решение задачи, производя заданный в ее условии расчет.

Исходя из условия прочности, можно производить три вида расче­тов: а) проверочный, при котором проверяется, выполнено ли условие прочности σ≤[σ] (или n≤[n]); б) определение допускаемой нагрузки; в) проектный, при котором определя­ются необходимые размеры попереч­ных сечений бруса, обеспечивающие заданную прочность.

Пример 10. Жесткий брус OD (рис. 16, а), шарнирно закрепленный в точке О, удерживается в равновесии с помощью стержней 1 и 2. В точке D
брус нагружен силой F = 40 кН. Оп­ределить напряжения в поперечных
сечениях обоих стержней, если а = 1 м, площади поперечных сечений соответственно А₁ = 4 см² и А_г = = 6 см².

 

Рис. 16

 

Решение. Разрезаем стержни и заменяем их действие на брус силами N₁ и N₂ (рис. 16, б). В данном случае реакции шарнира О нас не интересуют, а в уравнение моментов относительно точки О (урав­нение равновесия статики)

входят обе неизвестные силы. Следовательно, задача один раз статиче­ски неопределима (уравнение проекций на оси х и у ничего не дают, так как в них войдут еще две неизвестные составляющие реакции шарнира О).

Для того чтобы составить дополнительное уравнение перемеще­ний, допустим, что после нагружения бруса узел С опустился на Δ l₂, а узел В – на Δ l₁. Из подобия треугольников ОВВ₁ и ОСС₁ полу­чим уравнение перемещений:

Так как Δ l₁ = N₁l₁ / (E А₁) и Δ l₂ = N₂l₂(E A₂), a l₂ = 2 l₁, что сле­дует из рассмотрения тех же треугольников ОВВ₁ и ОСС₁, то уравнение (2) примет вид

Подставив в это уравнение значения A₁ = 4 см² и А₂ = 6 см², находим, что N₂ = 1,5 N₁.

Решив последнее уравнение совместно с уравнением (1), получим

Теперь легко найти напряжения в поперечных сечениях стержней, помня, что А₁ = 4 см² = 400 мм² и А₂ = 6 см² = 600 мм²,

Пример 11. Абсолютно жесткий брус (рис. 17, а) опирается на шарнирно неподвижную опору О и прикреплен к двум стержням в точках В и С с помощью шарниров. Определить: а) нормальные силы, возникшие в стержнях; б) допускаемую нагрузку [F], приравняв боль­шее из напряжений, возникшее в одном из стержней, допускаемому напряжению [σ] = 160 Н/мм².

Рис. 17

 

Решение. Разрезаем стержни и вводим искомые силы N₁ и N₂ (рис. 17, б), составляем уравнение равновесия, приняв за центр момен­тов шарнир О:

которое после деления обеих частей на а приобретает вид

В результате удлинения стержней брус займет новое положение (рис. 17, б). Из подобия треугольников OBB₁ и ОСС₁ следует про­порция Δ l₁ /2а = Δ l ₂/5 а, из которой получаем зависимость между удлинениями стержней: 5 Δ l₁ – 2 Δ l ₂ = 0.

Выразим в этом уравнении перемещения шарниров В (Δ l₁) и (Δ l ₂)
по формуле Гука:

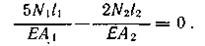
Умножим обе части уравнения на Е и, подставив числовые значения величин l₁ = 4·10³ мм, l ₂ = 3·10³ мм, А₁ = 20·10² мм² и А₂= 10·10² мм², получим уравнение перемещений в окончательном виде:

5 N₁ – 3 N₂ = 0

Решив совместно уравне­ния (1), (2), находим значения искомых сил:

По найденным значениям внутренних сил находим напря­жения в сечениях стерж­ней:

σ₂>σ₁, следовательно, допускаемую нагрузку определяем по напря­жениям в стержне 2, помня, что [σ] = 160 и 16·10^-5 [F] = 160·[F] = 10⁶ Н = 1000 кН.

Третью задачу (№ 81-90) следует решать после изучения темы «Практические расчеты на срез и смятие» и разбора решенного примера.

Детали для соединения отдельных элементов машин (заклепки, болты, штифты и т. п.) воспринимают нагрузки, перпендикулярные их продольной оси. Расчеты таких деталей базируются на следующих основных допущениях: 1) в поперечном сечении возникает только один внутренний силовой фактор – поперечная сила Q; 2) касательные напряжения в поперечном сечении распределены по его площади равно­мерно; 3) если соединение осуществлено несколькими одинаковыми деталями (болтами и т. п.), то принимается, что все они нагружены одинаково.

Условие прочности при срезе

где τ_ср – расчетное касательное напряжение среза, возникающее в поперечном сечении рассчитываемой детали; k – количество срезов од­ной заклепки; Q – поперечная сила; i – число болтов, заклепок и т. п.; [τ_ср] = (0,25...0,35)σ_т – допускаемое напряжение среза, где σ_т – предел текучести материала болта.

Расчетная формула на смятие имеет вид

где А_см – расчетная площадь смятия; А_см= δ_min·d; [σ_см] – допускае­мое напряжение на смятие, принимают по табл. 7; δ _min – минималь­ная толщина соединяемых деталей; d – диаметр заклепки.

Таблица 7

Материал конструкции	Допускаемые напряжения, Н/мм2
при продольных отверст.	при сверленых отверст.
[τ]ср	[σ] см	[τ]ср	[σ] см
Сталь Ст2 Сталь СтЗ

 

В заклепочном соединении проверяется прочность листа по формуле

где m – число заклепок, попадающих в одно поперечное сечение листа; b – ширина листа; δ – толщина листа; d – диаметр заклепок.

Пример 12. Определить высоту h и диаметр d головки стержня, нагруженного растягивающей силой F (рис. 18). Допускае­мые напряжения для стали СтЗ при продавленных отверстиях прини­маем [σ] = 140Н/мм² (см. табл. 7).

 

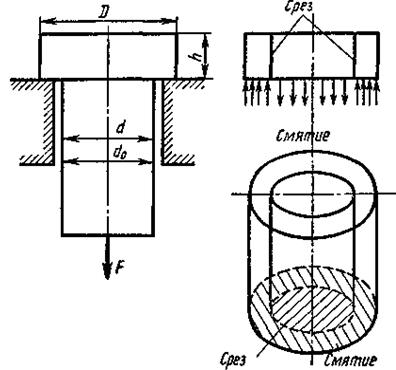
Рис. 18

 

Решение. Определяем допускаемую нагрузку из 'условия проч­ности стержня на растяжение:

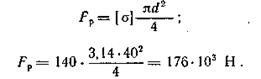
Определяем высоту головки из условия прочности на срез, принимая [ τ ]_ср= 100Н/мм².

Определяем диаметр опорной поверхности головки из условия ее прочности на смятие, принимая [σ]_см= 280 Н/мм².

 

 

К решению четвертой задачи (№ 91-100) следует приступить после изучения темы «Кручение» и разбора решенного примера.

В соответствии с Международной системой единиц (СИ) заданную в условии частоту вращения n (об/мин) необходимо выразить в единицах угловой скорости (рад/с), применив формулу ώ = π n /30. Тогда зависимость между передаваемой мощностью Р (кВт), угловой скоростью ώ (рад/с) и внешним моментом М_вр (Н·м), скручивающим вал, запишется в виде M_вр = Р/ώ.

Допускаемый угол закручивания на практике обычно задается в град/м, поэтому для перевода в единицы СИ это значение необходимо умножить на π/180°. Например, если дано [φ°] = 0,4 град/м, то 0,4 град/м = 0,4π/180° = 0,007 рад/м = 7·10^-3 рад/м.

Пример 13. Для стального вала (рис. 19, а)определить из условия прочности требуемые диаметры каждого участка и углы закручивания этих участков. Угловую скорость вала принять ώ = 100 рад/с, допус­каемое напряжение [τ] = 30 МПа, модуль упругости сдвига G = 0,8·10⁵ Н/мм².

Рис. 19

 

Решение. Вал вращается с постоянной угловой скоростью, сле­довательно, система вращающих моментов уравновешена. Мощность, подводимая к валу без учета потерь на трение, равна сумме мощ­ностей, снимаемых с вала:

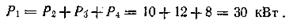
Определяем вращающие моменты на шкивах:

Для построения эпюр крутящих моментов проведем базовую (нуле­вую) линию параллельно оси вала и, используя метод сечений, най­дем значения крутящего момента на каждом участке, отложим най­денные значения перпендикулярно базовой линии.

Вал имеет три участка, гра­ницами которых являются сечения, в которых приложены внешние моменты. В пределах каждого участка значение крутящего момента сохраняется постоянным (рис. 19, б):

Кручением называют такой вид деформации бруса, при котором в его поперечных сечениях возникает только один внутренний силовой фактор – крутящий момент М_к.

Крутящий момент в каком-либо поперечном сечении вала численно равен алгебраической сумме внешних моментов, действующих на остав­ленную часть вала в плоскостях перпендикулярно оси вала и приложен­ных по одну сторону от рассматриваемого сечения.

При вычислении крутящих моментов целесообразно установить правило знаков: рассматривая любую из оставленных частей бруса со стороны сечения, внешние моменты, действующие по ходу часовой стрелки, считать положительными, действующие против хода часовой стрелки – отрицательными.

Из условия прочности диаметр вала на первом участке опреде­ляем по формуле

откуда

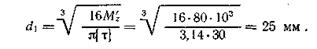
На втором участке

На третьем участке

Вычисляем полярные моменты инерции сечений вала:

Углы закручивания соответствующих участков вала:

Пятую задачу контрольной работы (№ 101-110) следует решать после изучения темы «Изгиб» и внимательного разбора примеров 14 и 15 настоящего пособия.

При прямом поперечном изгибе в поперечных сечениях балки возникает два внутренних силовых фактора – поперечная сила Q_y и изгибающий момент М_х. Поперечная сила, возникающая в произволь­ном поперечном сечении, численно равна алгебраической сумме всех внешних сил (если все силы параллельны оси у), действующих на балку по одну сторону от рассматриваемого сечения.

Изгибающий момент в произвольном поперечном сечении численно равен алгебраической сумме моментов всех внешних сил, действующих на балку по одну сторону, от рассматриваемого сечения относительно той точки продольной оси балки, через которую проходит рассматривае­мое сечение.

Для отыскания опасного сечения строят эпюры Q_y и М_х, исполь­зуя метод сечения.

Условимся о правиле знаков: внешняя сила F, стремящаяся сдвинуть левую часть балки вверх относительно правой или (что то же самое) правую часть вниз относительно левой, вызовет возникновение положительной поперечной силы (рис. 20, a).

Рис. 20

 

Внешняя сила или момент, изгибающие балку таким образом, что сжатые волокна находятся сверху балки (рис. 20, б), вызывают положи­тельный изгибающий момент, который на эпюре М_х откладывается вверх от оси абсцисс, т. е. в сторону сжатых волокон, иначе можно сказать, что эпюры изгибающих моментов строятся на сжатом волокне.

Для балок, имеющих много участков нагружения, т. е. нагружен­ных комбинацией нагрузок, целесообразно строить эпюры по характер­ным сечениям, а именно: вычислять поперечные силы и изгибающие моменты только для сечений, в которых эпюры претерпевают изменения, а затем, зная закон изменения эпюры между найденными сечениями, соединить их соответствующими линиями. К характерным относятся сечения, в которых приложены сосредоточенные силы или моменты, а также сечения, где начинается или кончается распределенная нагрузка.

Для того чтобы вычислить поперечную силу и изгибающий момент в произвольном сечении, необходимо мысленно рассечь плоскостью в этом месте балку и часть балки (любую), лежащую по одну сторону от рассматриваемого сечения, отбросить. Затем по действующим на оставленную часть балки внешним силам надо найти искомые значения Q_y и М_х, причем знак их надо определить по тому действию, какое оказывают внешние силы на оставленную часть балки в соответствии с принятым ранее правилом знаков.

При построении эпюры слева направо отбрасывается правая часть балки, a Q_y и М_x находятся по силам, действующим на левую часть. При построении эпюры справа налево, наоборот, отбра­сывается левая часть, a Q_y и М _х определяются по силам, дей­ствующим на правую часть балки.

Для построения эпюр необходимо запомнить следующие правила.

1. На участке балки, где отсутствует распределенная нагрузка, эпюра Q_y – прямая, параллельная базовой линии, а эпюра М_х – наклонная прямая.

2. Под сосредоточенной силой на эпюре Q_y наблюдается скачок, численно равный приложенной внешней силе, а на эпюре М_х – излом.

3. В точке приложения сосредоточенной пары сил на эпюре мо­мента происходит скачок на размер момента этой пары, а эпюра Q_y не претерпевает изменения.

4. На участке действия равномерно распределенной нагрузки эпюра Q_y выражается наклонной прямой, а эпюра М_г – параболой, обращенной выпуклостью навстречу действию распределенной нагрузки.

5. Если на участке действия распределенной нагрузки эпюра пересекает базовую линию, то в этом сечении изгибающий момент принимает экстремальное значение.

6. Если на границе действия распределенной нагрузки не прило­жено сосредоточенных сил, то на эпюре Q_y участок, параллельный оси абсцисс, переходит в наклонный без скачка, а параболическая и наклонная части эпюры М_х сопрягаются плавно без изгиба.

7. Изгибающий момент в концевых сечениях балки всегда равен нулю, за исключением случая, когда в концевом сечении действует сосредоточенная пара сил. В этом случае изгибающий момент в конце­вом сечении балки равен моменту действующей пары сил.

8. В сечении, соответствующем заделке, Q_y и М_х численно равны опорной реакции и реактивному мо­менту.

Решать задачу рекомендуется в такой последовательности:

1) определить реакции опор балки (по двум уравнениям моментов: од­
но – относительно левой опоры, вто­рое – относительно правой), а затем
обязательно проверить правильность решения по уравнению проекций на
ось, перпендикулярную балке;

2) построить эпюру поперечных сил;

3) построить эпюру изгибающих моментов (для этого целесооб­разно использовать метод построения по характерным, сечениям);

4) по эпюре изгибающих моментов определить расчетный (наи­больший по абсолютному значению) изгибающий момент, выразив его в Н·мм;

5) в выражении условия прочности σ = M_и/W_x≤[o] принять σ = [σ] и определить требуемый осевой момент сопротивления попереч­ного сечения балки;

6) выразить значение W_х в мм³ (при подстановке в расчетную формулу W_x = M_x / [σ] значения М_х выражаются в Н·мм, а значения [σ] – в Н/мм², результат получим в мм³) и с помощью таблиц соответ­ствующих ГОСТов по найденному значению W_x подобрать необходимый номер профиля швеллера (ГОСТ 8240-72) или двутавра (ГОСТ 8239-72); при решении задач контрольной работы, т.е. в учебных целях, можно использовать старые ГОСТы 1956 г. (ГОСТ 8209-56 «Балки двутавровые» и ГОСТ 8240-56 «Швеллеры»), которые имеются в любом сборнике задач по сопротивлению материалов, изданном до 1976 г.

Пример 14. Для балки (рис. 21, а) построить эпюры поперечных сил, и изгибающих моментов, если сосредоточенные силы F₁ = 4 кН и F = 8 кН, момент М = 11 кН·м, расстояние а=2м, b = 4м, с = 3м.

Рис. 21

 

Решение. Определим опорные реакции:

откуда

откуда

Для проверки составляем сумму проекций всех сил на вертикаль­ную ось у:

Строим эпюру поперечных сил (рис. 21, b).

В сечении К: Q_{y K} = – F₁ = – 4 кН.

В сечении A: Q_yAлев= – F₁ = – 4 кН;

Q_yA_прав= – F₁+R_A= – 4 + 7 = 3 кН.

В сечении А: на эпюре Q_y получается скачок на величину реак­ции R_A.

В сечении D:

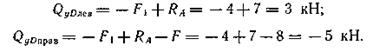
В сечении В: Q_yB= – R_B = – 5 кН.

Строим эпюру изгибающих моментов по характерным сечениям К, A, D, В (рис. 21, в).

В сечении К изгибающий момент М_хК= 0, так как в этом сечении нет сосредоточенного момента.

В сечении А рассмотрим левую часть, на которую действует сосредоточенная сила F₁

В сечении В действует сосредоточенный момент М:

В сечении D рассмотрим правую часть, на которую действует сила R_B и сосредоточенный момент М:

Соединим полученные точки эпюры на участках DB и AD наклон­ными прямыми.

 

СПИСОК ЛИТЕРАТУРЫ

 

1. Чернилевский, Д. В., Лаврова, Е. В., Романов, В. Н. Техническая механика. – М., 1982.

2. Техническая механика / Л. А. Эрдеди, Ю. А. Медведев, И. В. Ани­кин, А. С. Чуйков. – М., 1980.

3. Аркуша, А. И., Фролов, М. И. Техническая механика. – М., 1983.

4. Аркуша, А. И. Руководство к решению задач по теоретической механике. – М., 1976.

5. Файн, А. М. Сборник задач по теоретической механике. – М., 1978.