В гидравлике различают малые и большие отверстия. Малым называют отверстие, вертикальный размер которого существенно (в 5-10 раз) меньше напора истечения. В этом случае скорость вытекающей струи по сечению отверстия можно считать одинаковой. Если.струя касается только кромки отверстия, то стенку, в которой выполнено отверстие, в гидравлическом смысле называют тонкой. Такой случай истечения наблюдается при острой кромке отверстия, либо при толщине стенки менее половины диаметра отверстия.
 |
Струя на выходе из отверстия в тонкой стенке сжимается, достигая на некотором (около 0.5 диаметра отверстия) расстоянии наименьшего сечения, называемого сжатым (рис.16). Степень сжатия струи оценивается коэффициентом сжатия
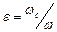(2.5)
где wc - площадь сжатого сечения струи, м2;
 |
w - площадь отверстия, м2.
Насадками называют патрубки длиной 3-4 диаметра, приставляемые к отверстию для увеличения 
расхода или придания струе особых свойств, например, дальнобойности (рис.17).
 |
При входе в цилиндрический насадок струя сначала сужается, отрываясь от стенок и образуя циркуляционую зону с пониженным давлением (ниже атмосферного в случае истечения в атмосферу), а затем постепенно расширяется и заполняет все сечение насадка (рис.18). Сжатия струи при выходе из насадка не происходит, поэтому коэффициент сжатия для выходного сечения насадка e =1.
В инженерной практике скорость u и расход Q через отверстия и насадки определяют по формулам
(2.6)
(2.7)
где j - коэффициент скорости, учитывающий снижение скорости за счет гидравлического сопротивления отверстия и насадка;
Н - напор истечения, м;
w - площадь отверстия или выходного сечения насадка, м2;
m - коэффициент расхода, связанный с другими коэффициентами истечения соотношением 
, откуда видно, что m учитывает снижение расхода, вызываемое гидравлическими сопротивлениями и сжатием струи.
В общем случае коэффициенты истечения m, j, e зависят от числа Рейнольдса. При развитом турбулентном режиме истечения (при Re >l05) численные значения коэффициентов становятся постоянными и равными:
для малых круглых отверстий в тонкой стенке
j =0.97 e =0.64 m =0.62
для внешнего цилиндрического насадка
jн =0.82 eн =1 mн =0.82
Сравнение указанных коэффициентов для отверстия и насадка показывает, что присоединение к отверстию внешнего цилиндрического насадка обеспечивает при развитом турбулентном режиме истечения увеличение расхода (mн > m) примерно на 30 %.
При истечении жидкости под уровень (рис.20) напор истечения (действующий напор) определяется разностью полных напоров до и после насадка (отверстия)
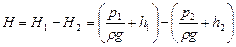(2.8)
2.6. Контрольные задания по разделу "Основы гидродинамики"
Задача 1.
По трубопроводу диаметром d =100 мм движется жидкость На напорном водоводе постоянного диаметра в водопроводных колодцах А и В, расположенных на расстоянии l друг от друга, установлены манометры МA и МB (рис.19), показывающие давление pа и pB. Гидравлический уклон равен i, пьезометрический ip. Высота колодцев ZA и ZB. Пользуясь данными таблицы 3, определить величины, отмеченные в ней знаком вопроса.
Таблица 3
| № вар | ZA, м | ZB , м | pA, кПа | pB, кПа | l, км | i | iP | Направление течения |
| 1.1 | ? | - | ? | |||||
| 2.1 | - | ? | ? | |||||
| 1,8 | ? | - | ? | |||||
| ? | 1.5 | - | 0.002 | От А к В | ||||
| ? | - | 0.0018 | От А к В | |||||
| ? | 1.6 | - | 0.0019 | От А к В | ||||
| 3.2 | - | ? | ? | |||||
| ? | 1.5 | - | 0.002 0202. | От B к A | ||||
| ? | 3.1 | - | 0.0043 | От B к A | ||||
| ? | 2.6 | - | 0.0015 | От B к A |
Задача 2.
Определить расход воды, протекающий через насадок (рис.20) по данным таблицы 4. Во всех вариантах задан диаметр входного сечения. Значение давления дано в атмосферах, p A= 1атм =101325Па.
Таблица 4
| № вар. | Тип насадка | H 1, м | H 2 м | d, мм | l, мм | q, град | p 1, атм | p 2, атм |
| Цилиндр | p A | p ИЗБ=0.2 | ||||||
| Цилиндр | - | p A | p АБС=1.2 | |||||
| Цилиндр | - | p ВАК=0.3 | p A | |||||
| № вар. | Тип насадка | H 1, м | H 2 м | d, мм | l, мм | q, град | p 1, атм | p 2, атм |
| Цилиндр | p ИЗБ=0.2 | p A | ||||||
| Сходящийся конус | - | 13°24' | p A | p ИЗБ=0.7 | ||||
| Расходящийся конус | - | p АБС= 1.2 | p А | |||||
| Расходящийся конус | p А | p А | ||||||
| Расходящийся конус | - | p А | р АБС=0.7 | |||||
| Сходящийся конус | 13°24' | p AБС=1.5 | p ИЗБ=0.5 | |||||
| Цилиндр | p ВАК=0.2 | p А |
РАСЧЕТ ТРУБОПРОВОДОВ
Одной из основных задач практической гидравлики является нахождение потерь напора (потерь удельной механической энергии) при движении жидкостей. В зависимости от потерь напора в гидравлических системах назначаются диаметры трубопроводов, высота расположения баков, напор и мощность насосов. При расчете трубопроводов определяют потерю напора по длине трубопровода, местные потери напора и полную потерю напора.
Полная потеря напора hтр на преодоление сил гидравлического трения при течении жидкости складывается из потерь напора по длине hl и суммы местных потерь напора hj:
(3.1)
Для вычисления потерь напора по длине используется, как правило, формула Дарси-Вейсбаха, местных потерь - формула Вейсбаха. Подобным задачам нужно уделить самое пристальное внимание, так как они лежат в основе расчета отопительных, вентиляционных сетей, систем теплогазоснабжения.
Потеря напора по длине
Потеря напора по длине вызвана тормозящим действием стенок, приводящим к вязкостному трению частиц и струек жидкости друг о друга вдоль трубопровода. Такие потери при равномерном течении пропорциональны длине потока и для круглых труб (каналов) определяются по формуле Дарси-Вейсбаха
(3.2)
где l - коэффициент гидравлического трения или коэффициент Дарси;
l, d - соответственно длина и внутренний диаметр трубы (канала), м;
u - средняя скорость потока, м/с.
Коэффициент трения l в общем случае зависит от числа Рейнольдса Re и относительной шероховатости стенок трубы D/ d (где D средняя высота выступов шероховатости стенок или абсолютная шероховатость).
При ламинарном режиме (Re <2300) коэффициент трения вычисляется по теоретической формуле Пуазейля
(3.3)
Подставляя это выражение для l в формулу (3.2) и расписывая число Рейнольдса Re = ud / n, получаем, что в ламинарном потоке потери напора по длине пропорциональны средней скорости в первой степени (hl ~ u).
В турбулентных потоках выделяют ядро, т.е. область, где протекает основная масса жидкости, и тонкий слой с ламинарным режимом течения (ламинарный подслой) с существенно меньшими скоростями, который формируется вблизи стенок русла или трубы. В зависимости от толщины этого слоя в большей или меньшей степени проявляется влияние физической шероховатости стенок на весь поток. Как следствие, во всем спектре потоков с турбулентным режимом течения различают области гидравлически гладких и гидравлически шероховатых труб (стенок). Кроме этого, в области гидравлически шероховатых труб выделяют также зону квадратичного сопротивления.
Гидравлически гладкие трубы
Трубу или стенку считают гидравлически гладкой, если соблюдается условие 2300£ Re £10 d /D. В этом случае прилегающий к стенке ламинарный подслой турбулентного потока покрывает выступы шероховатости и жидкость не испытывает дополнительных завихрений, вызванных неровностью стенок. В области гидравлически гладких труб, как и в ламинарном режиме, l зависит только от числа Рейнольдса. Для таких потоков l вычисляется по эмпирической формуле Блазиуса
(3.4)
Гидравлически шероховатые трубы
С увеличением числа Рейнольдса, например за счет повышения скорости течения, толщина ламинарного подслоя турбулентного потока уменьшается и при Re >10 d / D выступы шероховатости оголяются. Они начинают вносить дополнительные возмущения (вихри) в турбулентное ядро потока, что приводит к возрастанию потерь напора; в этом случае труба (стенка) называется гидравлически шероховатой. Коэффициент гидравлического трения для таких потоков определяется по формуле Альтшуля:
(3.5)
Зона квадратичного сопротивления
Формула (3.5) указывает на увеличение коэффициента гидравлического трения l с возрастанием относительной шероховатости D/ d стенок. При достаточно больших числах Рейнольдса (Re >100000)коэффициент l, не зависит от Re и определяется лишь относительной шероховатостью D/ d стенок, а потери напора по длине становятся пропорциональными квадрату средней скорости hl ~ u 2:. Такая категория турбулентных потоков относится к области квадратичного сопротивления.
Итак, для вычисления потерь напора по длине необходимо предварительно выявить область сопротивления, к которой будет относиться поток (область ламинарного движения, область гладких или шероховатых стенок турбулентного движения), а затем определить коэффициент гидравлического трения l по формулам, которые соответствуют этим областям. После этого потеря напора рассчитывается по формуле Дарси-Вейсбаха.
Для трубопроводов представляющих систему труб с разным диаметром потери напора по длине определяются для каждого i -го участка (hl) i. Общая потеря напора по длине будет складываться из потерь на каждом участке
(3.6)
где 
- коэффициент гидравлического сопротивления на i -м участке.
Местные потери напора
Местные потери напора (удельной механической энергии жидкости) возникают на коротких участках трубопровода с препятствиями для потока, называемыми местными сопротивлениями. К местным гидравлическим сопротивлениям относятся внезапное расширение и сужение труб, вентили, задвижки, клапаны, колена, решетки, сетки и другие элементы гидравлических систем, изменяющие конфигурацию стенок трубы или канала. Местные сопротивления вызывают изменение скорости движения жидкости по величине и направлению, что почти всегда приводит к отрыву потока (транзитной струи) от стенок и возвратному течению жидкости около них с образованием циркуляционных зон. Поглощение механической энергии потока в циркуляционных зонах, где она расходуется на создание и поддержание вращения жидкости, и составляет, в основном, местные потери напора.
В инженерных расчетах для определения местных потерь используется формула Вейсбаха, согласно которой потеря выражается в долях от скоростного напора
(3.7)
где x - коэффициент местного сопротивления;
u - средняя скорость потока за местным сопротивлением, м/с.
При подсчете местных потерь напора используются справочные эмпирические значения x, которые зависят от геометрии местных сопротивлений и числа Рейнольдса Re. Однако, в подавляющем большинстве случаев в местных сопротивлениях присутствует развитый турбулентный режим. При этом значения коэффициентов приобретают постоянные значения, которые зависят только от геометрических особенностей узлов, создающих местные гидравлические сопротивления.
Местные потери напора определяются как сумма потерь в локальных узлах, в каждом из которых они должны рассчитываться отдельно
Следует обратить внимание на то, что, согласно формуле Вейсбаха (3.7), скоростной напор выражается через среднюю скорость течения u, которая имеет место за узлом, в котором рассчитывается потеря напора. Часто в задачах с неравномерным движением жидкости (трубопроводы переменного сечения) местные потери требуется привести к одному скоростному напору. Для приведения привлекается уравнение неразрывности (2.1), согласно которому скоростной напор на одном участке 
может быть выражен через скоростной напор на другом участке 
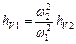(3.8)
