Объемным расходом (расходом) Q называют объем жидкости V, протекающий через живое сечение потока в единицу времени – Q = V / t.
Живым сечением потока называют поверхность, в каждой точке которой линии тока жидкости пересекают ее под прямым углом (рис.13). Для потока, в котором положение линий тока является параллельным (параллельноструйное движение) или это положение достаточно близко к параллельному (плавноизменяющееся движение) живое сечение является плоским (рис.13,б). Характеристикой живого сечения является его площадь w.
Средней скоростью потока u называется отношение расхода жидкости в некотором живом сечении к площади этого сечения u = Q / w.
 |
Часть контура поперечного сечения русла или трубы, непосредственно соприкасающаяся с жидкостью называется смоченным периметром, который характеризуется длиной c (рис.14).
Отношение площади сечения потока к длине смоченного периметра называется гидравлическим радиусом RГ
Для круглых труб, полностью заполненных водой, гидравлический радиус RГ связан с геометрическим радиусом r соотношением: r =2 RГ.
Уравнение постоянства расхода
Уравнение постоянства расхода (его называют еще уравнением неразрывности) представляет собой условие сплошности потока несжимаемой жидкости. Оно показывает, что для установившегося течения объемные расходы жидкости в двух разных поперечных сечениях одного и того же потока будут равны. Уравнение выражает частный случай закона сохранения вещества и записывается так
(2.1)
В уравнении (2.1) u 1, u 2 и w 1, w 2 обозначают соответственно среднюю скорость и площадь живого сечения на двух разных участках потока. Уравнение неразрывности показывает, что расход по длине потока не изменяется и равен произведению средней скорости u потока на площадь живого сечения w. Следует твердо усвоить, что это уравнение справедливо для установившихся (не изменяющихся во времени) потоков несжимаемой жидкости и при отсутствии в ней разрывов (газовых и паровых полостей).
Режимы движения жидкости
Различают два основных режима течения жидкости: ламинарный (слоистый) и турбулентный (вихревой). При ламинарном режиме частицы жидкости движутся по параллельным траекториям без перемешивания. По этой причине жидкость движется отдельными слоями, и поток имеет слоистую структуру. Турбулентное движение характеризуется пульсацией давления и скоростей частиц, что вызывает интенсивное перемешивание жидкости в потоке, то есть вихревое движение.
Критерием режима течения является число Рейнольдса
(2.2)
где u – средняя скорость потока, м/с;
d – внутренний диаметр трубы (канала), м;
n - кинематический коэффициент вязкости жидкости, м2/с.
В случае течения жидкости по трубам некругового сечения при вычислении числа Рейнольдса по формуле (2.2) вместо диаметра трубы dГ используется гидравлический диаметр, определяемый соотношением
где RГ – гидравлический радиус, м;
w – площадь живого сечения, м2;
c – смоченный периметр, м.
В инженерной практике расчетный режим течения определяют, сравнивая число Рейнольдса Re с его критическим значением Reкp, которое соответствует смене режимов движения жидкости. Для равномерных потоков жидкости в трубах (каналах) круглого сечения принимают Reкp =2300. При Re < Reкр =2300 поток будет ламинарным, а при Re > Reкр =2300 – турбулентным.
Из выражения (2.2) следует, что числа Рейнольдса малы и, следовательно, режим является ламинарным, при низких скоростях течения в каналах незначительного поперечного сечения (в порах грунта, капиллярах) или при движении жидкостей с большой вязкостью (нефть, масло, битумы). Турбулентный режим в природе и технике встречается чаще. Его закономерностям подчиняется движение воды в реках, ручьях, каналах, системах газоводоснабжения и водоотведения, а также течение бензина, керосина и других маловязких жидкостей в трубах.
Уравнение Бернулли
Уравнение Бернулли для установившегося потока реальной жидкости выражает закон сохранения энергии и имеет вид
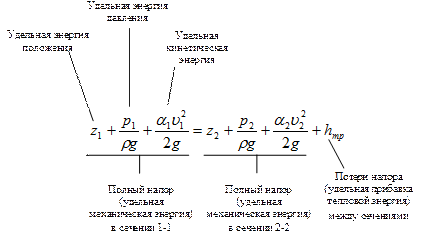
(2.3)
где z - расстояние от произвольно выбранной горизонтальной плоскости сравнения О-О до центра рассматриваемого сечения потока (рис.15), м;
р - давление в сечении на оси потока, Па;
r - плотность жидкости, кг/м3;
a - коэффициент кинетической энергии (коэффициент Кориолиса). На основании опытов значения коэффициента оказываются равными a =1,1¸1,15, однако, обычно принимают a =1.0;
u - средняя скорость потока, м/с;
g - ускорение свободного падения, м/с2;
hтр - суммарные потери напора между сечениями 1-1 и 2-2 на преодоление гидравлических сил трения, м.
Индексы 1 и 2 указывают номер сечения, к которому относится величина. Сечения, связываемые уравнением, выбираются на участках с плавноизменяющимся движением жидкости, хотя между сечениями движение может быть и резкоизменяюшимся.
Слагаемые уравнения (2.3) измеряются в единицах Дж/Н (энергия/сила) и поэтому выражают тот или иной вид удельной энергии (энергии, отнесенной к единице веса - силы тяжести жидкости). Названия видов удельной энергии указаны над уравнением. Механическую энергию единицы веса жидкости (удельную энергию) в гидравлике принято называть напором: 
- пьезометрическим, 
- скоростным, 
- полным.
Из уравнения следует, что в случае отсутствия теплообмена потока с внешней средой полная удельная энергия (включая тепловую) неизменна вдоль потока и поэтому изменение одного вида энергии приводит к противоположному по знаку изменению другого. В этом состоит энергетический смысл уравнения Бернулли.
Геометрический смысл уравнения (2.3) заключается в том, что его слагаемые могут быть измерены в единицах длины (Дж/Н=м) геометрической z, пьезометрической 
, с коростной и потерянной hтр высотами, сумма которых для любого сечения является постоянной величиной.
Измерение указанных высот простейшими приборами (мерной линейкой, пьезометром, трубкой Пито) и графическая иллюстрация уравнения Бернулли показаны на рис.15. Для большей наглядности рисунка каждая трубка Пито установлена в такой точке сечения потока, в которой удельная кинетическая энергия 
равна средней по сечению удельной кинетической энергии . Для каждого сечения уровень жидкости в трубке Пито выше, чем в пьезометре, на величину скоростного напора .
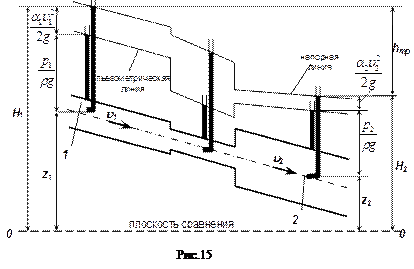
Линия, соединяющая уровни жидкости в пьезометрах, называется пьезометрической. Она располагается над плоскостью сравнения на расстоянии 
и иллюстрирует изменение по длине потока удельной потенциальной энергии (пьезометрического напора). Линия, проведенная через уровни жидкости в трубках Пито, отражает распределение полной удельной механической энергии (полного напора) вдоль потока и называется напорной. Падение полного напора hтр, приходящееся на единицу длины l потока, называется гидравлическим уклоном
(2.4)
Линии удельных энергий (напорная и пьезометрическая) дают наглядное представление о переходе одного вида энергии в другой по длине потока и позволяют при решении многих задач инженерной практики установить значения, причины и степень изменяемости основных параметров движения жидкости. Линии удельных энергий строятся в соответствии с нижеприведенными правилами, вытекающими из уравнения Бернулли.
1. Напорная линия постоянно понижается по течению (если на рассматриваемом участке нет насоса) ввиду необратимого преобразования механической энергии в тепловую при преодолении потоком сил гидравлического трения. Причем уклон линии (потери напора hтр) тем больше, чем меньше сечение участка потока (рис.15).
2. Пьезометрическая линия в отличие от напорной, может не только понижаться, но и повышаться по течению. Это происходит при расширении потока (рис.15) и объясняется уменьшением скорости и кинетической энергии, часть которой в силу сохранения баланса переходит в потенциальную энергию . Другими словами, увеличение скорости потока приводит к снижению давления по сечению и наоборот. Если давление в трубопроводе меньше атмосферного, пьезометрическая линия опускается ниже оси трубопровода. При истечении жидкости в атмосферу пьезометрическая линия проходит через центр тяжести выходного сечения канала (трубопровода).
3. Расстояние между напорной и пьезометрической линиями равно скоростному напору, а поэтому обратно пропорционально диаметру сечения трубы в четвертой степени. На тех участках потоков, где трубопровод имеет постоянное сечение, средние скорости одинаковы. Поэтому здесь линии удельных энергий (напорная и пьезометрическая) параллельны друг другу. Для потоков в конфузорных (конически сходящихся) патрубках они расходятся, а в диффузорных (конически расходящихся) - сходятся. В баках и водоемах, где жидкость неподвижна, линии энергий совпадают со свободной поверхностью, если на ней действует атмосферное давление.
