При воздействии на диэлектрик световой волны происходит поляризация диэлектрика. Электрическое поле световой волны вызывает смещение электронных оболочек атомов относительно ядер, в результате атомы приобретают электрический дипольный момент. Такая поляризация диэлектрика называется электронной поляризацией. Наряду с электронной поляризацией возможны ионная (смещение ионов относительно друг друга) и ориентационная (вращение дипольных молекул) поляризации.
Количественно поляризация диэлектрика описывается вектором поляризации 
, представляющим собой электрический дипольный момент единицы объема среды, наведенный внешним полем. Наведенная поляризация есть ответная реакция среды на внешнее воздействие, которое описывается вектором электрической напряженности 
световой волны. Если величина поля меняется, то поляризация диэлектрика изменяется аналогичным образом. Связь величин 
и 
в линейной оптике имеет вид:
(i,k=1,2,3), (7.1)
где αik – компоненты тензора диэлектрической восприимчивости среды. Соотношение (7.1) называется линейным материальным уравнением. Тензор диэлектрической восприимчивости симметричен и соответствующим поворотом системы координат может быть приведен к диагональному виду: 
. (7.2)
Для изотропных сред и кристаллов, относящихся к кубической симметрии α11=α22=α33=α и соотношение (7.1) примет простой вид:
= α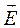 
. (7.3)
Рассмотрим анизотропные кристаллы. Одноосным кристаллам соответствует случай α11=α22≠α33 (оптическая ось совпадает с осью Z), а двуосным кристаллам - α11≠α22≠α33.
В интенсивном световом поле, создаваемом лазером, диэлектрические восприимчивости становятся зависимыми от напряженности поля световой волны и выражение (7.1) превращается в нелинейное материальное уравнение: Pi= 
(7.4)
Нелинейная поляризация среды (7.4) и обуславливает зависящие от интенсивности оптического излучения нелинейно-оптические явления. Если разложить 
, входящий в (7.4) в ряд по степеням напряженности 
, то получим:
= 
(7.5)
где αik – линейная восприимчивость (тензор 2-го ранга); χikj – квадратичная нелинейная восприимчивость (тензор 3-го ранга); θikjm – кубичная нелинейная восприимчивость (тензор 4-го ранга).
Подставляя (7.5) в (7.4) получаем следующее нелинейное материальное уравнение: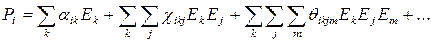 
(7.6)
или в сокращенной условной форме записи:
Р=aЕ+cЕ2+qЕ3+…=Р(л)+ Р(2)+ Р(3)+… (7.7)
где Р(л) – компонента вектора линейной поляризации, Р(2) – вектор квадратичной поляризации и Р(3) - вектор кубичной поляризации.
Для кристаллов обладающих центром симметрии, а также для жидкостей и газов тензор квадратичной восприимчивости равен нулю, поэтому нелинейность указанных сред определяется в первом порядке кубичной восприимчивостью θ. Эти среды соответственно, называются кубично нелинейными.
В кристаллах с квадратичной восприимчивостью основной вклад в его нелинейную поляризацию вносит квадратичная поляризация, и эти кристаллы называются квадратичными нелинейными средами.
7.2 Генерация оптических гармоник,
суммарных и разностных частот
Пусть на квадратично-нелинейный диэлектрик падает световая волна с частотой w, а напряженность электрического поля в кристалле задается выражением: E= E0cos(ωt -kx). (7.8)
Тогда подставляя (7.8) в уравнение (7.7) получаем:
Р(2)=cЕ2=χE02cos2(ωt -kx)= 
+ cos(2ωt -2kx). (7.9)
Здесь первое слагаемое связано с эффектом оптического выпрямления, а второе слагаемое описывает волну поляризации на частоте 2w. Волна поляризации на частоте 2w может привести к переизлучению света на этой же частоте, т.е. к генерации второй оптической гармоники. В результате этого явления в данной среде распространяются две волны - на частоте ω и на частоте 2ω. Схематично процесс генерации второй оптической гармоники показан на рис. 7.1.
Рис. 7.1. Схема генерации второй оптической гармоники в квадратично-нелинейном кристалле.
В свою очередь вследствие взаимодействия этих двух волн в квадратично-нелинейном кристалле возможна генерация на суммарных и разностных частотах.
Пусть теперь в квадратично-нелинейный кристалл входят две волны одинаковой амплитуды на частотах ω1 и ω2. Рассмотрим поле создаваемое этими волнами: E= E0[cos(ω1t –k1x)+ cos(ω2t –k2x)]. (7.10)
Подставляя (7.10) в выражение для квадратичной поляризации Р(2)=cЕ2, и, проведя несложные алгебраические преобразования, получим:
Р(2)=cЕ02[cos(ω1t –k1x)+ cos(ω2t –k2x)]2=cЕ02[cos2(ω1t –k1x)+ cos2(ω2t –k2x)+ 2cos(ω1t –k1x)cos(ω2t –k2x)]=cЕ02[1+ cos(2ω1t –2k1x)/2+ cos(2ω2t –2k2x)+cos[(ω1+ω2)t –(k1+ k2)x)]+ cos[(ω1–ω2)t –(k1 – k2)x)].
В полученном выражении первое слагаемое суммы связано эффектом оптического выпрямления, второе и третье слагаемые описывают волны поляризации на частотах 2ω1 и 2ω2, а четвертое и пятое слагаемые относятся к волнам поляризации на частотах (ω1+ω2) и (ω1-ω2), т.е. на суммарных и разностных частотах. В частности, при распространении и взаимодействии в квадратично – нелинейной среде двух волн на частотах ω и 2ω возможна генерация третьей оптической гармоники на частоте 3ω, генерация четвертой оптической гармоники на частоте 4ω и т.д. (рис.7.2.). В принципе, при необходимости получения высших гармоник, можно добавить третий и четвертый каскады преобразования.
Рис.7.2. Схема генерация в нелинейной среде суммарных
и разностных частот.
Аналогичным образом, рассматривая распространение интенсивной световой волны (7.8) на частоте ω в кубично – нелинейной среде, получим для кубичной поляризации:
Р(3)=qЕ3= qE03cos3(ωt -kx)= 
cos(ωt –kx)+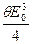 
cos(3ωt –3kx). (7.11)
В этом случае, наряду с основной частотой, в полученном выражении присутствует волна поляризации на частоте 3ω, которая приводит к генерации третьей оптической гармоники. Волна поляризации на частоте w обуславливает, как будет показано далее, эффект самофокусировки света.
