Принципы организации баз данных 4 страница

Доказательство формальных математических утверждений (теорем) – последовательность корректных выводов, ведущих от условия к заключению. Алгебра логики помогает доказывать теоремы (дает общие подходы и методы доказательства).

Общий подход к доказательству теорем методом от противного, обратных и противоположных теорем можно формализовать с помощью алгебры логики.

 

6 Лекция: Логические вентили, схемы, структуры

 

Рассматриваются основные теоретические (математические, логические) понятия и сведения, касающиеся базовых логических элементов и структур – логических вентилей, логических (переключательных) схем, логической базы аппаратуры ЭВМ и их оптимальной структуры, оптимизации их структур.

Любой, самый примитивный компьютер – сложнейшее техническое устройство. Но даже такое сложное устройство, как и все в природе и в технике, состоит их простейших элементов. Любой компьютер, точнее, любой его электронный логический блок состоит из десятков и сотен тысяч так называемых вентилей (логических устройств, базовых логических схем), объединяемых по правилам и законам (аксиомам) алгебры вентилей в схемы, модули.

Логический вентиль (далее – просто вентиль) – это своего рода атом, из которого состоят электронные узлы ЭВМ. Он работает по принципу крана (отсюда и название), открывая или закрывая путь сигналам.

Логические схемы предназначены для реализации различных функций алгебры логики и реализуются с помощью трех базовых логических элементов (вентилей, логических схем или так называемых переключательных схем). Они воспроизводят функции полупроводниковых схем.

Работу вентильных, логических схем мы, как и принято, будем рассматривать в двоичной системе и на математическом, логическом уровне, не затрагивая технические аспекты (аспекты микроэлектроники, системотехники, хотя они и очень важны в технической информатике).

Логические функции отрицания, дизъюнкции и конъюнкции реализуют, соответственно, логические схемы, называемые инвертором, дизъюнктором и конъюнктором.

Логическая функция "инверсия", или отрицание, реализуется логической схемой (вентилем), называемой инвертор.

Принцип его работы можно условно описать следующим образом: если, например, "0" или "ложь" отождествить с тем, что на вход этого устройства скачкообразно поступило напряжение в 0 вольт, то на выходе получается 1 или "истина", которую можно также отождествить с тем, что на выходе снимается напряжение в 1 вольт.

Аналогично, если предположить, что на входе инвертора будет напряжение в 1 вольт ("истина"), то на выходе инвертора будет сниматься 0 вольт, то есть "ложь" (схемы на рисунке 1).

Функцию отрицания можно условно отождествить с электрической схемой соединения в цепи с лампочкой (рис. 2), в которой замкнутая цепь соответствует 1 ("истина") или х = 1, а размыкание цепи соответствует 0 ("ложь") или х = 0.

 

Рис. 1. Принцип работы инвертора

 

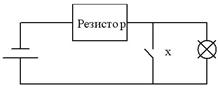
Рис. 2. Электрический аналог схемы инвертора

 

Дизъюнкцию 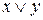реализует логическое устройство (вентиль) называемое дизьюнктор (рис. 3):

Рис. 3. Принцип работы дизъюнктора

Дизъюнктор условно изображается схематически электрической цепью вида (рис. 4)

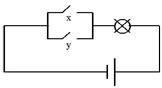
Рис. 4. Электрический аналог схемы дизъюнктора

 

Конъюнкцию 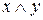реализует логическая схема (вентиль), называемая конъюнктором (рис. 5):

Рис. 5. Принцип работы конъюнктора

 

Конъюнктор можно условно изобразить схематически электрической цепью вида (рис. 6.6)

Рис. 6. Электрический аналог схемы конъюнктора

 

Схематически инвертор, дизъюнктор и конъюнктор на логических схемах различных устройств можно изображать условно следующим образом (рис. 7). Есть и другие общепринятые формы условных обозначений.

Рис. 7. Условные обозначения вентилей (вариант)

 

Из указанных простейших базовых логических элементов собирают, конструируют сложные логические схемы ЭВМ, например, сумматоры, шифраторы, дешифраторы и др. Большие (БИС) и сверхбольшие (СБИС) интегральные схемы содержат в своем составе (на кристалле кремния площадью в несколько квадратных сантиметров) десятки тысяч вентилей. Это возможно еще и потому, что базовый набор логических схем (инвертор, конъюнктор, дизъюнктор) является функционально полным (любую логическую функцию можно представить через эти базовые вентили), представление логических констант в них одинаково (одинаковы электрические сигналы, представляющие 1 и 0) и различные схемы можно "соединять" и "вкладывать" друг в друга (осуществлять композицию и суперпозицию схем).

Таким способом конструируются более сложные узлы ЭВМ – ячейки памяти, регистры, шифраторы, дешифраторы, а также сложнейшие интегральные схемы.

Пример. В двоичной системе таблицу суммирования цифры x и цифры y и получения цифры z с учетом переноса p в некотором разряде чисел x и y можно изобразить таблицей вида

x	y	z	p

Эту таблицу можно интерпретировать как совместно изображаемую таблицу логических функций (предикатов) вида

Логический элемент, соответствующий этим функциям, называется одноразрядным сумматором и имеет следующую схему (обозначим ее как или – если мы хотим акцентировать именно выбранный, текущий i -й разряд) (рис. 8):

Рис. 8. Схема одноразрядного сумматора

 

Пример. "Черным ящиком" называется некоторое закрытое устройство (логическая, электрическая или иная схема), содержимое которого неизвестно и может быть определено (идентифицировано) только по отдельным проявлениям входа/выхода ящика (значениям входных и выходных сигналов). В "черном ящике" находится некоторая логическая схема, которая в ответ на некоторую последовательность входных (для ящика) логических констант выдает последовательность логических констант, получаемых после выполнения логической схемы внутри "черного ящика". Определим логическую функцию внутри "черного ящика" (рис. 9), если операции выполняются с логическими константами для входных последовательностей (поразрядно). Например, х = 00011101 соответствует последовательности поступающих значений: "ложь", "ложь", "ложь", "истина", "истина", "истина", "ложь", "истина".

 

Рис. 9. Схема "черного ящика 1"

 

Из анализа входных значений (входных сигналов) х, у и поразрядного сравнения логических констант в этих сообщениях с константами в значении z – результате выполнения функции в "черном ящике", видно, что подходит, например, функция вида .

Действительно, в результате "поразрядного" сравнения сигналов (последовательностей значений "истина", "ложь") получаем следующие выражения (последовательности логических констант):

.

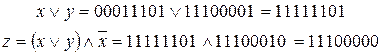Пример. Попробуйте самостоятельно выписать функцию для "черного ящика"? указанного на рис. 10:

 

Рис. 10. Схема "черного ящика 2"

 

Важной задачей (технической информатики) является минимизация числа вентилей для реализации той или иной схемы (устройства), что необходимо для более рационального, эффективного воплощения этих схем, для большей производительности и меньшей стоимости ЭВМ.

Эту задачу решают с помощью методов теоретической информатики (методов булевой алгебры).

Пример. Построим схему для логической функции . Схема, построенная для этой логической функции, приведена на рис. 11.

Рис. 11. Схема для функции 1

 

Пример. Определим логическую функцию , реализуемую логической схемой вида (рис. 12):

 

Рис. 12. Схема для функции 2

 

Искомая логическая функция, если выписать ее последовательно, заполняя "верх" каждой стрелки, будет иметь следующий вид: .

7 Лекция: Базовые алгоритмические структуры

 

Рассматриваются основные понятия об алгоритме в программах и алгоритмизации решения задач.

"Алгоритм" является базовым основополагающим понятием информатики, а алгоритмизация (программирование) – основным разделом курса информатики (ядром курса). Понятие алгоритма, как и понятие информации, точно определить невозможно. Поэтому встречаются самые разнообразные определения – от "наивно-интуитивных" ("алгоритм – это план решения задачи") до "строго формализованных" (нормальные алгоритмы Маркова).

В качестве рабочего определения алгоритма возьмем следующее определение.

Алгоритм – это упорядоченная совокупность точных (формализованных) и полных команд исполнителю алгоритма (человек, ЭВМ), задающих порядок и содержание действий, которые он должен выполнить для нахождения решения любой задачи из рассматриваемого класса задач.

Алгоритм удовлетворяет следующим основным свойствам:

1. Конечность (дискретность) команд и выполняемых по ним действий алгоритма.

2. Выполнимость в определенной операционной среде (в определенном классе исполнителей).

3. Результативность отдельных команд и всего алгоритма.

4. Применимость алгоритма ко всем возможным входным данным конкретного класса задач.

5. Определенность (детерминированность) команд и всего алгоритма для всех входных данных.

6. Формализованное, конструктивное описание (представление) команд алгоритма.

7. Минимальная полнота системы команд алгоритм.

8. Непротиворечивость любых команд алгоритма на любом наборе входных данных.

Любой алгоритм ориентирован на некоторый общий метод решения класса задач и представляет собой формализованную запись метода, процедуры.

Алгоритм, записанный на некотором алгоритмическом, формальном языке, состоит из заголовка алгоритма (описания параметров, спецификаций класса задач) и тела алгоритма (последовательности команд исполнителя, преобразующих входные параметры в выходные).

Для записи, исполнения, обмена и хранения алгоритмов существуют различные средства, языки, псевдокоды – блок-схемы (структурные схемы алгоритмов), структурограммы (схемы Нэсси-Шнайдермана), Р-схемы, школьный алгоритмический язык (ШАЯ), различные языки программирования.

В качестве языка описания алгоритмов нами далее используется визуальный графический способ описания с помощью блок-схем, так как он более нагляден.

 

Более подробно с процессом описания алгоритмов можно ознакомиться в методических указаниях:

Лантратов О.И. Методические указания и задания к практическим занятиям по теме “Структурные схемы алгоритмов” /О.И. Лантратов, Е.Б. Ивушкина. – Шахты: Изд-во ДГАС, 1997.

 

8 Лекция: Данные, их типы, структуры и обработка

Рассматриваются основные понятия о данных к алгоритмам, их базовые типы и структуры, вопросы их использования в алгоритмизации задач.

Любая актуализация информации опирается на какие-то данные, любые данные могут быть каким-то образом актуализированы.

Данные – это некоторые сообщения, слова в некотором заданном алфавите.

Пример. Число 123 – данное, представляющее собой слово в алфавите из десяти натуральных цифр; число 12,34 – данное, представляющее собой слово в алфавите из десяти натуральных цифр и десятичной запятой; текст "математика и информатика – нужные дисциплины", – данное в алфавите из символов русского языка и знаков препинания, включая пробел.

Текущее (то есть рассматриваемое в данный момент времени) состояние данных называют текущим значением данных или просто значением.

До разработки алгоритма (программы) необходимо выбрать оптимальную для реализации задачи структуру данных. Неудачный выбор данных и их описания может не только усложнить решаемую задачу и сделать ее плохо понимаемой, но и привести к неверным результатам. На структуру данных влияет и выбранный метод решения.

Пример. При решении системы линейных алгебраических уравнений можно воспользоваться методом Крамера (с помощью определителей) или методом Гаусса (с помощью последовательных исключений неизвестных). Метод Крамера потребует при реализации примерно в 3 раза больше операций, чем метод Гаусса, и поэтому им никогда не пользуются при расчетах на ЭВМ.

Тип данных характеризует область определения значений данных.

Задаются типы данных простым перечислением значений типа, например как в простых типах данных, либо объединением (структурированием) ранее определенных каких-то типов – структурированные типы данных.

Пример. Зададим простые типы данных "специальность", "студент", "вуз" следующим перечислением:

- специальность = (филолог, историк, математик, медик);

- студент = (Петров, Николаев, Семенов, Иванова, Петрова);

- вуз = (МГУ, РГУ, КБГУ).

Значением типа "студент" может быть Петров.

Пример. Опишем структурированный тип данных "специальность_студента":

- специальность_студента=(специальность, студент).

Значением типа "специальность_студента" может быть пара (историк, Семенов).

Для обозначения текущих значений данных используются константы – числовые, текстовые, логические.

Часто (в зависимости от задачи) рассматривают данные, которые имеют не только "линейную" (как приведенные выше), но и иерархическую структуру.

Пример. Структуру "вуз" можно задать иерархической структурой, состоящей, например, из следующих уровней: "Ректорат", "Деканаты и подразделения", "Кафедры", "Отделы", "Преподаватели и сотрудники".

В алгоритмических языках есть стандартные типы, например, целые, вещественные, символьные, тестовые и логические типы. Они в этих языках не уточняются (не определяются, описываются явно) и имеют соответствующие описания с помощью служебных слов.

Пример. В школьном алгоритмическом языке (ШАЯ), например, целые, вещественные, символьные, текстовые (литерные, стринговые) и логические типы данных описываются ключевыми словами цел, вещ, сим, лит, лог. В языке Паскаль – аналогичными ключевыми словами integer, real, char, string, boolean.

Каждый тип данных допускает использование определенных операций со значениями типа ("с типом").

Пример. Для целого типа данных назовем операции "=" (присвоение), "+", "–", "*", "=" (сравнение на равенство), "≠", "<", ">", "≤", "≥".. Для вещественного типа данных еще и операция "/" (деление). Для символьного типа данных – только ":=", "=", "≠", "<", ">", "≤", "≥". Например, сравнение "а"<"b" означает, что символ "а" предшествует символу "b" то есть код буквы "a" меньше кода буквы "b" (коды символов приводятся, например, в таблице ASCII – Аmerican Standard Code for Information Interchange, американский стандарт кодирования для обмена данными). Для текстового (литерного) типа данных можно использовать еще и операцию конкатенации (присоединения справа) текстов "+". Например, "аб"+"ба" даст новый текст "абба". Для данных логического типа определены логические операции и отношения сравнения. Например, на Basic для логических переменных a, b, c можно записать корректное выражение: a and b or (c or not a).

Для описания переменных, значениями которых могут быть лишь символы, тексты, используются соответствующие ключевые слова: на ШАЯ – сим, лит, на Паскале – char, string. Текстовые (символьные) константы обычно заключают в апострофы.

 

Наиболее часто используемая структура данных – массив.

Одномерный массив (вектор, ряд, линейная таблица) – это совокупность значений некоторого простого типа (целого, вещественного, символьного, текстового или логического типа), перенумерованных в каком-то порядке и имеющих общее имя. Для выделения конкретного элемента массива необходимо указать его порядковый номер в этом ряду.

Пример. Последовательность чисел 89, –65, 9, 0, –1.7 может образовывать одномерный вещественный массив размерности 5, например, с именем x вида: x[1] = 89, x[2] = –65, x[3] = 9, x[4] = 0, x[5] = –1.7.

Значение порядкового номера элемента массива называется индексом элемента.

Пример. Можно ссылаться на элемент х[4], элемент х[i], элемент x[4+j] массива х. При текущих значениях переменных i = 2 и j = 1 эти индексы определяют, соответственно, 4-й, 2-й и 5-й элементы массива.

Для обозначения (нового типа объектов) массивов в алгоритмических языках обычно вводится специальное служебное слово.

Пример. В ШАЯ – это слово "таб", после которого приводится имя массива и в квадратных скобках его размерность, например, для одномерного массива – в виде [m:n], где m – номер первого элемента массива (часто 1), n – номер последнего элемента (шаг перебора элементов равен 1). В Basic имеется соответствующее слово dim (dimension). Вышеуказанная последовательность из пяти чисел описывается на ШАЯ в виде: вещ таб x[1:5], а на Basic – dim x(5).

Двумерный массив (матрица, прямоугольная таблица) – совокупность одномерных векторов, рассматриваемых либо "горизонтально" (векторов-строк), либо "вертикально" (векторов-столбцов) и имеющих одинаковую размерность, одинаковый тип и общее имя.

Матрицы, как и векторы, должны быть в алгоритме описаны служебным словом (например, таб или dim), но в отличие от вектора, матрица имеет описание двух индексов, разделяемых запятыми: первый определяет начальное и конечное значение номеров строк, а второй – столбцов.

Пример. Если матрица x описана в виде dim x(5,3), то определяется таблицу из 5 строк (от 1-й до 5-й строки) и 3 столбцов (от 1-го до 3-го столбца) вида:

 

(столбец 1)	(столбец 2)	(столбец 3)
x11	x12	х13	(строка 1)
x21	x22	х23	(строка 2)
х31	х32	х33	(строка 3)
х41	x42	х43	(строка 4)
х51	x52	х53	(строка 5)

 

Для актуализации элемента двумерного массива нужны два его индекса – номер строки и номер столбца, на пересечении которых стоит этот элемент.

Пример. Элемент х(3,2) – элемент на пересечении 3-й строки и 2-го столбца массива х.

9 Лекция: Методы разработки и анализа алгоритмов

Рассматриваются основные понятия о методах проектирования (нисходящем, восходящем, модульном, структурном) и разработки алгоритмов (программ), тестирование и верификация алгоритма, трассировка алгоритма.

Нисходящим проектированием алгоритмов, проектированием алгоритмов "сверху вниз" или методом последовательной (пошаговой) нисходящей разработки алгоритмов называется такой метод составления алгоритмов, когда исходная задача (алгоритм) разбивается на ряд вспомогательных подзадач (подалгоритмов), формулируемых и решаемых в терминах более простых и элементарных операций (процедур). Последние, в свою очередь, вновь разбиваются на более простые и элементарные, и так до тех пор, пока не дойдём до команд исполнителя. В терминах этих команд можно представить и выполнить полученные на последнем шаге разбиений подалгоритмы (команд системы команд исполнителя).

Восходящий метод, наоборот, опираясь на некоторый, заранее определяемый корректный набор подалгоритмов, строит функционально завершенные подзадачи более общего назначения, от них переходит к более общим, и так далее, до тех пор, пока не дойдем до уровня, на котором можно записать решение поставленной задачи. Этот метод известен как метод проектирования "снизу вверх".

Структурные принципы алгоритмизации (структурные методы алгоритмизации) – это принципы формирования алгоритмов из базовых структурных алгоритмических единиц (следование, ветвление, повторение), используя их последовательное соединение или вложение друг в друга с соблюдением определённых правил, гарантирующих читабельность и исполняемость алгоритма сверху вниз и последовательно.

Структурированный алгоритм – это алгоритм, представленный как следования и вложения базовых алгоритмических структур. У структурированного алгоритма статическое состояние (до актуализации алгоритма) и динамическое состояние (после актуализации) имеют одинаковую логическую структуру, которая прослеживается сверху вниз ("как читается, так и исполняется"). При структурированной разработке алгоритмов правильность алгоритма можно проследить на каждом этапе его построения и выполнения.

Теорема (о структурировании). Любой алгоритм может быть эквивалентно представлен структурированным алгоритмом, состоящим из базовых алгоритмических структур.

Одним из широко используемых методов проектирования и разработки алгоритмов (программ) является модульный метод (модульная технология).

Модуль – это некоторый алгоритм или некоторый его блок, имеющий конкретное наименование, по которому его можно выделить и актуализировать. Иногда модуль называется вспомогательным алгоритмом, хотя все алгоритмы носят вспомогательный характер. Это название имеет смысл, когда рассматривается динамическое состояние алгоритма; в этом случае можно назвать вспомогательным любой алгоритм, используемый данным в качестве блока (составной части) тела этого динамического алгоритма. Используют и другое название модуля – подалгоритм. В программировании используются синонимы – процедура, подпрограмма.

Свойства модулей:

- функциональная целостность и завершенность (каждый модуль реализует одну функцию, но реализует хорошо и полностью);

- автономность и независимость от других модулей (независимость работы модуля-преемника от работы модуля-предшественника; при этом их связь осуществляется только на уровне передачи/приема параметров и управления);

- эволюционируемость (развиваемость);

- открытость для пользователей и разработчиков (для модернизации и использования);

- корректность и надежность;

- ссылка на тело модуля происходит только по имени модуля, то есть вызов и актуализация модуля возможны только через его заголовок.

Свойства (преимущества) модульного проектирования алгоритмов:

- возможность разработки алгоритма большого объема (алгоритмического комплекса) различными исполнителями;

- возможность создания и ведения библиотеки наиболее часто используемых алгоритмов (подалгоритмов);

- облегчение тестирования алгоритмов и обоснования их правильности;

- упрощение проектирования и модификации алгоритмов;

- уменьшение сложности разработки (проектирования) алгоритмов (или комплексов алгоритмов);

- наблюдаемость вычислительного процесса при реализации алгоритмов.

Тестирование алгоритма – это проверка правильности или неправильности работы алгоритма на специально заданных тестах или тестовых примерах – задачах с известными входными данными и результатами (иногда достаточны их приближения). Тестовый набор должен быть минимальным и полным, то есть обеспечивающим проверку каждого отдельного типа наборов входных данных, особенно исключительных случаев.

Пример. Для задачи решения квадратного уравнения ax ² + bx + c = 0 такими исключительными случаями, например, будут:

1) a = b = c = 0;

2) a = 0, b, c – отличны от нуля;

3) D = b ² – 4 ac < 0 и др.

Тестирование алгоритма не может дать полной (100%-ой) гарантии правильности алгоритма для всех возможных наборов входных данных, особенно для достаточно сложных алгоритмов.

Полную гарантию правильности алгоритма может дать описание работы и результатов алгоритма с помощью системы аксиом и правил вывода или верификация алгоритма.

Пример. Составим алгоритм нахождения числа всех различных двоичных сообщений (двоичных последовательностей) длины n битов, используя при этом не более одной операции умножения, и докажем правильность этого алгоритма.

Вначале найдем число всех таких сообщений. Число двоичных сообщений длины 1 равно 2 = 2¹ (это "0" и "1"), длины 2 равно 4 = 2² ("00", "01", "10", "11"). Отправляясь от этих частных фактов, методом математической индукции докажем, что число различных сообщений длины n равно 2 ⁿ. Этот индуктивный вывод докажет правильность алгоритма.

Пусть это наше утверждение верно для n = k. Тогда для n = k + 1 получаем, что добавление каждого бита (0 или 1) к любому из 2 ^k сообщений длины k приведет к увеличению числа сообщений в 2 раза, то есть их число будет равно 2 × 2 ^k = 2 ^{k +1}, что и доказывает наше индуктивное предположение.

Составим теперь алгоритм вычисления числа x = 2 ⁿ с использованием операции умножения только один раз.

Прологарифмируем последнее равенство. Получим ln(x) = ln(2 ⁿ) = n ln(2).

Используя равенство exp(ln(x)) = x, получим, что exp(ln(x)) = x = exp(n ln(2)).

Остается теперь, только, записать простейший алгоритм вычисления числа x.