ВВЕДЕНИЕ
Вопросы изучения живых организмов и растительных объектов, а также процессы, происходящие на клеточном, молекулярном и генетическом уровне становятся все более актуальными с каждым днем. С этой целью в научных лабораториях разрабатываются методы по их исследованию и моделируются сложных явлений природы. К наиболее часто используемым методам исследования можно отнести экспериментальные и методы многомерной статистики. Они являются важной и неотъемлемой частью лабораторного эксперимента и позволяют достоверно выявить закономерности происходящих природных процессов, а также найти причинно-следственные связи между ними.
В научных исследованиях для получения достоверных данных эффективно используется метод массовых наблюдений. Данный метод основан на использовании большого количества повторностей в каждой экспериментальной группе. Материал, полученный в ходе лабораторного опыта, обрабатывают и анализируют, далее по полученным данным делают соответствующие выводы и устанавливают те или иные закономерности. Большое значение в достижении наибольшей точности результатов и выводов в ходе эксперимента имеет не только качество экспериментальных методик, но и правильная статистическая обработка, так как полученные результаты могут значительно варьироваться в пределах одной экспериментальной группы. Таким образом, выполнение статистического анализа экспериментально полученных данных расширяет возможности в познании биологических явлений природы, способствует объективной оценке полученных результатов, исключая возможность субъективной точки зрения исследователя, а также методической ошибки, которые возникают при выполнении эксперимента, и дает возможность экспериментатору сделать точные и корректные выводы и заключений в отношении изучаемого явления.
Предмет исследования – компьютерные технологии как способ обработки данных, полученные при лабораторном исследований.
Цель исследования – проанализировать возможности статистических программ при обработке данных, полученных в результате постановки лабораторного эксперимента.
Задачи исследования:
· Оценить методы математической статистики с точки зрения их возможностей и границ применения при планировании и обработки биохимического эксперимента.
· Изучить, имеющиеся статистические пакеты анализа.
· Освоить возможности решения задач прикладной статистики средствами Microsoft Excel (применения стандартных функций и пакета анализа данных) и известных статистических пакетов STATISTICA в области биохимии.
Компьютерные технологии имеют большое значение в статистической обработке данных. Это позволяет не только ускорить данный процесс в несколько раз, но и произвести его на более высоком качественном уровне.
ТЕОРЕТИЧЕСКИЕ АСПЕКТЫ ИСПОЛЬЗОВАНИЯ КОМПЬЮТЕРНЫХ ТЕХНОЛОГИЙ ПРИ ПРОВЕДЕНИИ ЛАБОРАТОРНОГО ИССЛЕДОВАНИЯ
Биометрия как наука и основные ее понятия
В последние годы все чаще для решения и моделирования поставленных задач используются компьютерные технологии. В связи с этим возросла потребность в высококвалифицированных специалистах, имеющих хорошую теоретическую базу и имеющие опыт работы с некоторыми программами. На сегодняшний день в учебных учреждениях появляются дисциплины, которые позволяют сформировать устойчивые умения, необходимые для обработки и представления результатов научной деятельности. Наука, которая занимается изучением методов сбора и токованием числовых данных называется статистика. Данная дисциплина имеет важное практическое значение, так как позволяет прогнозировать развития природных, социальных процессов и явлений. Со временем стали появляться более специализированные отрасли данной науки. Таким образом, на стыке двух самостоятельных наук: биология и статистика, - появляется биологическая статистика (или биометрия). Биометрия – эмпирическая наука, изучающая данные, полученные при постановке опыта путем выполнения некоторых математических вычислений. Выполнение данных операций без вычислительной техники и компьютерных технологий занимает очень много времени. Насколько это трудоемкий процесс мы можем убедиться, рассмотрев некоторые наиболее используемые понятия биометрии при характеристики исследуемого признака.
Основные понятия биометрии.
Очень часто в практической деятельности человека и при обработке данных, полученных в ходе научных исследований, используется средняя величина. Данная величина характеризует исследуемый признак и показывает, каким было бы значение переменной, если бы у всех объектов из выборки оно было бы одинаковым. Средне арифметическая вычисляется по формуле:
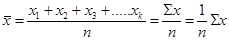 ,
,
где х1х2,..., xk - варианты совокупности; n— общее количество вариант.
Медиана (граница 50%-ного интервала) - значение, которое делит выборку пополам: в обе стороны от медианы в вариационном ряду располагается одинаковое число вариант. Эта величина зависит от накопления частот. Частоты накапливают до тех пор, пока не будет превышена половина суммы частот. Полученное наибольшее значение и есть медиана. Формула, по которой можно вычислить данное значение имеет следующий вид:
 ,
,
где xmin – минимальное значение предела интервала, где находится срединное значение; i - величина интервала; N-объем совокупности; Σn-суммарная численность до интервала, в котором находится срединное значение; Ne-численность интервала, где находится срединное значение.
Еще один статистический показатель это мода. Модой называется такая величина, которая наиболее часто встречается. Моду можно вычислить по формуле Пирсона:
 ,
,
где Ме – медиана; М-среднее значение признака.
Среднее квадратичное отклонение, - важнейшая характеристика в биологическом эксперименте. Данная величина является мерой рассеяния ряда распределения и определяется по формуле:

В некоторых экспериментах требуется очень высокая точность опыта. Например, в медико-биологических, токсикометрических и др. Ошибка в данных опытах не должна быть выше 1%, если значение ошибки превышает 1%, то точность результата является неудовлетворительной и нужно увеличивать количество повторностей.
Однако как бы исследователь ни старался точно выполнять все действия методики эксперимента, все равно на практике случаются ошибки, которые необходимо учитывать при обработке данных. Существует несколько типов ошибок.
Ошибка средней (mx) - показатель, на которое отличается среднее значение выборочной (опытной) совокупности от среднего значения генеральной совокупности, если распределение исследуемого параметра будет стремиться к нормальному значению. Основная ошибка среднего рассчитывается по формуле:

Более информативным и приемлемыми для сравнения групп используется коэффициент изменчивости, или вариации. Коэффициент изменчивости – это основное отклонение, выраженное в процентах от среднего значения, которое рассчитывается по формуле:

По полученным результатам делают вывод о характере и степени варьирования признака (таблица 1.1).
Таблица 1.1. Характер изменчивости признаков (по М.Л.Дворецкому)
| Коэффициент изменчивости, С | до 5% | 6-10% | 11-20% | 21-50% | более 50% |
| Характер изменчивости | слабая | умеренная | значительная | большая | очень большая |
Далее проверяют степень надежности результата:

Если значение t больше четырех, то среднее значение будет достоверным и соответственно можно сформулировать корректные выводы.
Определяют также процент расхождения между выборочной и генеральной средними - точность опыта (р,%), или ошибка наблюдений:
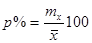
Этот параметр опыта показывает, на сколько процентов можно ошибиться, если утверждать, что генеральная средняя равна полученной выборочной средней.
Встатистике важным является показатель нормирования. Данный показатель используется для оценки вариант относительно к среднему значению данной группы по следующей формуле:

В зависимости от цели исследования значение может колебаться от x: ±0,5σ до х±1σ. Варианты со значением от 0,67σ до 2σ являются субнормальными, если значение равно более х± 2σ, то такие вариантыследует отнести к категории аномалий.
В биометрии существует такое понятие как ошибка репрезентативности. Эта ошибка, которая возникает не в ходе выполнения измерений или вычислений, а из-за случайного отбора при формировании группы.
При подсчете ошибки средней арифметической в небольших группах количество наблюдений (п) является «числом степеней свободы» - используется выражение (n-1), и тогда формула имеет вид:

Существует огромное количество формул вычисления ошибок эксперимента. Некоторые из них приведены ниже в качестве примера. Формула, по которой вычисляется средняя ошибка среднего квадратического отклонения:

Средняя ошибка коэффициента вариации (С):

Средняя ошибка показателя асимметрии:
 , или более точно:
, или более точно: 
Ошибку коэффициента эксцесса:
 , или
, или 
Сравнительный анализ полученных результатов сводится к оценке степени достоверности наблюдаемых между ними различий по следующей формуле:

где t - критерий достоверности. Его значение оценивается по таблицам вероятности Стъюдента. Если фактическое t больше табличного tst, то существует разница между двумя исследуемыми группами. Различие существенное, достоверное и его нельзя объяснить случайными причинами.
Для сравнения полученных результатов с ожидаемыми используют критерий хи-квадрат (χ2), который находится по формуле:

где, p – эмпирическая частота, p’ – ожидаемая частота. Значение χ2-теста заключается в том, чтобы узнать, подтверждается или опровергается гипотеза экспериментом. Если значений χ2, превышает табличное, то можно утверждать, что разница между фактическими и ожидаемыми результатами будет достоверной.
Так как большинство биологических объектов имеют огромное количество, нередко взаимосвязанных признаков, которые их характеризуют, например, вес, рост, возраст и др., то при исследовании комплекса показателей применяют дисперсионного анализа. Зависимость, при которой на каждое значение независимой переменной приходится только одно значение зависимой, называют функциональной. Однако в природе такая связь бывает очень редко. Обычно исследуемые объекты с одинаковыми значениями одного признака имеют разные значения по другим признакам. Такую связь называется корреляцией. Коэффициент корреляции показывает, насколько один исследуемый признак связан с другим (таблица 2). Коэффициент корреляции вычисляется по формуле:
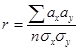
Таблица 1.2. Характеристика тесноты связи между признаками
| Коэффициент корреляции | Теснота связи | Коэффициент корреляции | Теснота связи |
| До 0,30 | Слабая | 0,71-0,90 | высокая |
| 0,31-0,50 | Умеренная | 0,91 и более | очень высокая |
| 0,51-0,70 | Значительная |
Так же необходимо найти квадратическую ошибку коэффициента корреляции:

Полученные показатели коэффициента корреляции оценивают с помощью критерия достоверности Стьюдента:
 или с помощью формулы
или с помощью формулы 
При оценке взаимосвязи величин очень важно найти аналитическое уравнение, которое будет соответствовать природе изучаемого явления для предсказания поведения независимой характеристики объекта при изменении зависимого параметра. Взаимосвязь между переменными величинами называется регрессией. Коэффициент регрессии, который определяется по следующим аналогичным формулам:
 -коэффициент регрессии Y.X;
-коэффициент регрессии Y.X;
 коэффициент регрессии X.Y,
коэффициент регрессии X.Y,
 и
и 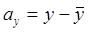 .
.
Для коэффициента регрессии также находят среднюю квадратическую ошибку:
 и
и 
Это основные формулы, применяемые в биометрии, которые используются при обработке данных, полученных в ходе биохимических исследований. Существует еще очень много статистических формул, однако все они, как мы уже убедились, состоят из нескольких математических действий, что осложняет вычисления исследователя и может привести к многочисленным ошибкам в расчетах. Исправление этих ошибок может отнять много времени при обработке большого количества данных. Таким образом, компьютерные технологии упрощают данный рутинный процесс в несколько раз, что позволяет более рационально использовать время, а также уменьшают вероятность ошибки, что дает уверенность в правильности полученных результатов и позволяет сделать корректные выводы.
Планирование и обработка биохимического эксперимента
В настоящее время существует множество информации и довольно сложно ориентироваться в этом бесконечном потоке знаний. Тогда возникает вопрос, каким образом можно получить интересующую информацию и подобрать нужную литературу, затратив при этом минимальное количество времени. Для этого существуют различные поисковые системы, которые значительно сокращают количество потраченного времени на подготовительном этапе. Так как прежде чем приступить к выполнению и планированию исследования, необходимо убедиться, не изучался ли данный вопрос ранее, каковы результаты проведенных исследований и какие критерии уже изучены. Чтобы больше осознать в полной мере необходимость информационных технологий в планировании эксперимента, необходимо понять, что представляет собой данный процесс.
Планированием эксперимента называется комплекс мероприятий, направленных на эффективную постановку опыта, главной целью которого является достижение максимальной точности измерений при проведении минимального количества опытов. При планировании опыта выделяют несколько этапов:
1. Предпланирование – этот этап включает в себя составление плана работы и его утверждение, выбор темы, формулировка рабочей гипотезы, информационная обработка плана и освоение методик.
Этот этап позволяет исключить возможность дублирования исследования, обеспечивает достоверность знаний и оригинальный подход к решению поставленных перед исследователем задач
2. Собственно процесс исследования – на данном этапе производится аналитический обзор литературы по данной проблеме, накопление данных, их систематизация и выработка представлений и проведение эксперимента. Эксперимент – набор действий и наблюдений, выполненных для проверки истинности или ложности выдвинутой гипотезы и установление причинно-следственных связей между изучаемыми феноменами.
Благодаря данному этапу исследователь может осознать насколько новой является данная тема и актуальны полученные результаты, сформулировать научно-практическую значимость.
3. Последний этап заключается в оформление результатов научного поиска – составление отчетов, написание статей.
Любой эксперимент основан на выполнении аналитического метода, Аналитические методы имеют критерии, определяющие пригодность метода:
· Специфичность – способность определить тот компонент, для определения которого данный способ исследования предназначен.
· Точность – качество измерений, отражающих близость полученных результатов, содержащих анализируемое вещество
· Сходимость (воспроизводимость в серии) представление о близости друг к другу результатов исследования выполненных в одних условиях в серии.
· Воспроизводимость – близость результатов, полученных при выполнении лабораторного аналитического исследования пробы в различных условиях. Данный параметр отражает степень разброса данных и позволяет выявить случайные ошибки.
· Правильность и неправильность - отличия от истинного значения
· Чувствительность – способность метода выявлять наименьшее значение анализируемого вещества. Оценивается величина отношения разности между показателями измерений прибора. Чем выше величина отношения, тем выше чувствительность метода.
· Предельная чувствительность – концентрация исследуемого вещества соответствующая минимальному измерению отличному от значения холостой пробы.
Интерпретация полученных результатов исследования производится вручную или с помощью компьютера. Один из способов оценки результатов это построение градуированной (калибровочной) кривой. Калибровочная кривая отображает тесную связь экстинкции, интенсивности излучения света и концентрации вещества в сериях стандартных растворов. Для построения градуированной кривой используются стандартные растворы.
Построение калибровочной кривой:
ü Приготовление стандартных растворов
ü Приготовление разведение стандартного вещества, который охватывает диапазон исследуемых концентраций и выходит за пределы максимального и минимального значения.
ü Из основного готовим маточные растворы
ü Для каждой концентрации стандартного раствора делаем 3-5 измерений
ü По полученным точкам строим график.
Для большей наглядности и точности лучше всего построить график. График показывает зависимость оптической плотности от концентрации раствора. Это будет более удобно при последующем определении концентрации изучаемого вещества в исследуемых пробах, что поможет рассчитать более правильную концентрацию рабочих растворов.






