Под балансом земляных масс понимается уравновешивание объемов вынутого грунта в районе выемок объемом засыпаемого грунта в районе насыпей.
Как правило, полного равенства этих объемов не бывает. Поэтому при составлении баланса земляных масс необходимо выделить участок на стройплощадке, на которых груз завозится извне или вывозится в отвал (если 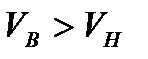 ).
).
На плане участка намечаем несбалансированные квадраты координатной сетки, в которые грунт будет завозиться из отвала. Целесообразно несбалансированные квадраты наметить в наиболее удаленных местах от линии нулевых работ.
Построение исходной матрицы
В данном случае поставщиками будут выемки, а потребителем – насыпи, продукцией является перевозимый грунт.
Составим исходную матрицу с учетом того, что планировка площадки в районе линии нулевых работ будет осуществлять бульдозер. Поэтому исключаем из рассмотрения участки выемки и насыпи, лежащие в районе линии нулевых работ и разрабатываемые бульдозером. В верхних правых углах клеток указываем расстояние перевозок с точностью до 1м.
Исходная матрица приведена в таблице 2.
| j | |||
| i | Bj Ai | ||
Таблица 2 Исходная матрица для решения транспортной задачи
Составление оптимального плана распределения земляных масс
Решение задачи распределения земляных масс выполнено двумя методами:
· двойного предпочтения
В k-й строке матрицы находим клетку с минимальной оценкой и отмечаем +, а затем столбцах. В первую очередь max загружаем клетки, отмеченные ++, затем +, затем все остальные. Преимущество отдаем клетке с минимальной оценкой. После этого функции перемножением объема на оценку и суммируем их, если план подлежит оптимизации, подсчитываем целевую функцию.
· аппроксимации Фогеля.
Составляем исходную матрицу тем же способом, что и выше. В каждой строке находим min оценку и ближнею к ней по величине. Разность между этими двумя значениями записывается справа в данной строчке. Аналогичные действия делаем и на столбце. Полученные числа рассматриваются в совокупности, выделим из них max, в строке (столбце) отмеченные max числом, начинаем загружать клетку с min оценкой. При наличии двух или более одинаковых чисел max можно принять любое число. Если в двух клетках столбца или строках оценка одинакова, то разность между ними равна 0, если план подлежит оптимизации, подсчитываем целевую функцию.
Целесообразность использования приведенных методов определяется с помощью формулы:
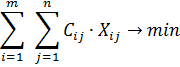
Целевая функция по методу двойного предпочтения равна 12300 у. е.;
Целевая функция по методу аппроксимации Фогеля равна 12300 у. е.;
Метод двойного предпочтения приведён в таблице 3, метод аппроксимации Фогеля приведён в таблице 4.
| j | ||||
| i | Bj Ai | ∑=67 | ||
| ++ 120 | + 290 | |||
| ∑=67 |
Таблица 3 Распределение земляных масс по методу двойного предпочтения
| j | ||||
| i | Bj Ai | |||
Таблица 4 Распределение земляных масс по методу аппроксимации Фогеля






