7.1 Общие сведения
В различных машинах и приборах широко применяются механизмы для воспроизведения вращательного движения с постоянным передаточным отношением между различно заданными в пространстве осями.
Такие механизмы носят название механизмов передачи вращательного движения тел, или сокращенно, механизмов передачи.
Применяются зубчатые, фрикционные и другие механизмы.
Простейшим механизмом передачи с твердыми звеньями является трехзвенный механизм, состоящий из двух подвижных звеньев, входящих в две вращательные и одну высшую пары.
Передаточным отношением механизма передачи называется отношение угловых скоростей ωi валов или их частот вращения. Передаточное отношение от вала 1 к валу 2
(7.1)
а от вала 2 к валу 1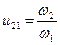 
Расположение осей трехзвенного механизма может быть параллельным, пересекающимся и перекрещивающимся. В курсовом проекте мы рассматриваем механизмы с параллельными и пересекающимися осями.
Кинематические схемы трехзвенных механизмов передач с параллельными осями, с внешним и внутренним зацеплением показаны на рис. 7.1 а, б. Они могут быть фрикционными или зубчатыми.
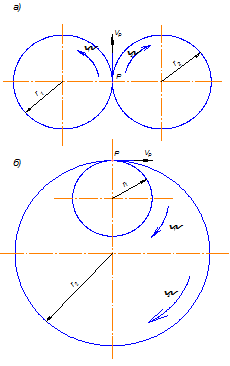
Рис. 7.1
В первом случае передача движения от одного звена к другому осуществляется за счет сил трения, во втором - посредством взаимодействия выступов конкретной формы, называемой зубом, одного звена, с соответствующим выступом парного звена.
В виду постоянства передаточного отношения угол поворота одного звена всегда строго соответствует углу поворота парного звена. Это означает, что на парных звеньях всегда имеются окружности, по которым звенья перекатываются друг по другу без скольжения, т.е. точки контакта имеют одинаковую скорость.
Если обозначить радиусы этих окружностей соответственно r1 и r2, то выражение (7.1) можно представить в виде:
(7.2)
где n1, n2 -частоты вращения первого и второго колеса соответственно.
Знак «плюс» соответствует внутреннему зацеплению (направления вращения звеньев совпадают); знак «минус» - внешнему (вращения звеньев противоположны).
Таким образом, передача вращения между параллельными осями с постоянным передаточным отношением всегда может быть осуществлена круглыми цилиндрическими колесами.
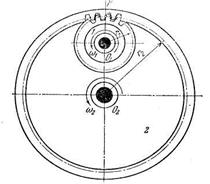
Простейший трехзвенный зубчатый механизм с параллельными осями состоит из двух круглых цилиндрических зубчатых колес. Каждое колесо представляет собой круглый цилиндр, на поверхности которого нарезаны зубья. Два зубчатых колеса, находящиеся в соприкосновении, своими зубьями образуют зубчатое зацепление внешнее (рис. 7.2, а) или внутреннее (рис. 7.2, б).
а) б) в)
| 
| 
|
Рис. 7.2
Угловые скорости колес в первом случае имеют разные знаки, во втором - одинаковые. Радиусы r1 и r2 являются радиусами центроид в относительном движении и называются начальными. По ним звенья 1 и 2 перекатываются друг по другу без скольжения. При определении передаточного отношения отношение радиусов удобно заменять отношениями чисел зубьев. Поэтому формулу (7.2) для зубчатого трехзвенного механизма можно представить в виде:
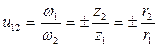(7.3)
Частным случаем зубчатого механизма с параллельными осями является механизм (рис. 7.2, в) с реечным зацеплением. Колесо 1, вращаясь вокруг оси О1 с угловой скоростью 
, приводит в прямолинейно поступательное движение рейку 2 со скоростью V2. Колесо имеет начальную окружность r1, а рейка- начальную прямую а-а. Точка Р является мгновенным центром вращения, а скорости 
и V2 связаны условием
(7.4)
Передачи с пересекающимися осями. Коническая передача применяется для передачи вращения между пересекающимися осями колес (рис. 7.3). Конические колеса перекатываются без скольжения по коническим поверхностям, называемыми начальными конусами.
а) б)
| 
|
Рис. 7.3
Основными параметрами конических зубчатых колес являются углы при общей вершине 
и 
начальных конусов. Углы 
и могут быть любыми, но на практике чаще всего применяются передачи с углом между осями равным 900.
Передаточное отношение конической передачи может быть выражено через углы 
и 
:
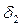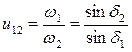(7.5)
7.2 Механизмы многоступенчатых зубчатых передач с неподвижными (параллельными и пересекающимися) осями
Для воспроизведения требуемых передаточных отношений в современных машинах и приборах часто применяются сложные механизмы, имеющие кроме входного и выходного звеньев, вращающихся вокруг заданных осей, промежуточные звенья, вращающиеся вокруг собственных осей. Сложный механизм передачи можно разделить на отдельные части – ступени, каждая из которых представляет собой трехзвенник с двумя низшими и одной высшей кинематическими парами.
Такие отдельные части механизма называют ступенями передачи.
Передаточное отношение от вала 1 к валу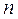 
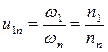(7.6)
а от вала 
к валу 1
Для передачи, у которой направления вращения крайних валов совпадает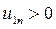 
, противоположны- 
.
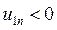Многоступенчатые механизмы получили название редукторов. Многоступенчатые передачи, у которых оси вращения колес неподвижны, носят название рядового соединения.
Рассмотрим рядовое соединение с параллельными осями, показанное на рис. 7.4, а. Входное зубчатое колесо 1 сцепляется с колесом 2. На ось О2 колеса 2 жестко насажено колесо 2/, которое сцепляется с колесом 3. На ось О3 колеса 3 жестко насажено колесо 3/ и т. д. Выходным является колесо 5.
Обозначим угловую скорость колеса 1 через 
, колеса 2 и 2/ – через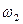 
, колес 3 и 3/ -через 
и т. д. Общее передаточное отношение механизма
Если число осей n, то
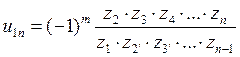(7.7)
где m - число внешних зацеплений.
Передаточное отношение сложной ступенчатой передачи есть произведение взятых со своим знаком передаточных отношений отдельных ступеней.
При передаче движения на большие расстояния или при необходимости воспроизведения передаточных отношений определенного знака, часто применяют рядовое соединение, состоящее из ряда последовательно соединенных колес, каждое из которых имеет собственную ось вращения (рис. 7.4, б).
Общее передаточное отношение такого рядового соединения, состоящего в рассматриваемом случае из четырех колес, равно:
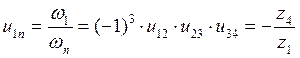(7.8)
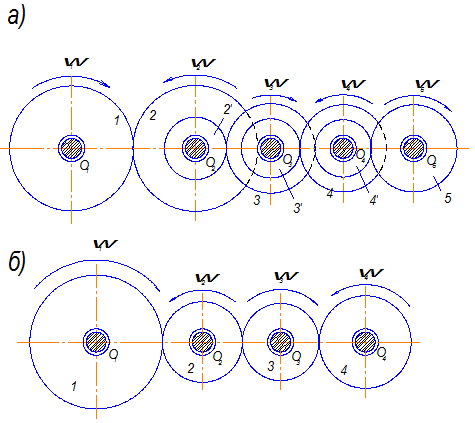
Рис. 7.4
Из формулы (7.8) следует, что величина передаточного отношения не зависит от числа зубьев промежуточных колес. Такие колеса называются паразитными.
В действительности они играют существенную роль, так как обеспечивают надлежащее вращение выходного вала, передают поток мощности, позволяют получить рациональные параметры колес при большом межцентровом расстоянии и между входным и выходным звеном.
Для определения передаточного отношения рядовой конической передачи (рис.7.5, а, б) используются формулы (7.7) и (7.8), а для направления вращения выходного вала вместо множителя (-1)m используется метод стрелок, суть которого состоит в следующем.
В месте касания колес 1 и 2 (см. рис. 7.5, а, б) поставим стрелки a и b. Причем, если стрелка а направлена от места касания, то и стрелка b должна быть направлена также от места касания или – к месту касания (см. рис.7.5,б). На колесах 2', жестко связанных с колесами 2, в местах касания с колесами 3 ставим стрелку того же направления, что и стрелка b. Тогда стрелка d для колеса 3 на рис. 7.5, а будет совпадать с направлением стрелки а, а на рис. 7.5, б – иметь противоположное направление, т. е. для рис. 7.5, а знак передаточного отношения следует считать положительным, а для рис. 7.5, б – отрицательным.
Передачи, у которых оси ведущих и ведомых валов совпадают, называют соосными передачами. Если передача увеличивает скорость вращения, то ее называют мультипликатором, если уменьшает – редуктором.
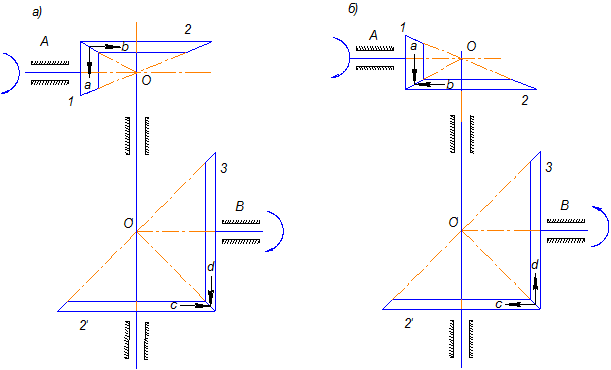
Рис. 7.5
Передачи, которые позволяют ступенчато или непрерывно изменять передаточное отношение, называются соответственно редукторами и бесступенчатыми редукторами или вариаторами.
7.3 Механизмы многоступенчатых передач с подвижными осями
Зубчатые механизмы, в составе которых имеются подвижные оси зубчатых колес, называются эпициклическими.
На рис. 7.6 а, б показаны простейшие эпициклические механизмы с внешним и внутренним зацеплением зубьев. Зубчатое колесо z2, ось которого перемещается в пространстве, называется сателлитом. Зубчатое колесо z1, вокруг оси которого вращается сателлит, называется солнечным или центральным. Звено Н, которое несет на себе ось сателлита, называется водилом.
В более сложных механизмах может быть несколько сателлитов, солнечных колес и водил. Наиболее распространенной схемой эпициклических механизмов является схема четырехколесного механизма (рис. 7.7, а), имеющая два сателлита z2 и z3, два солнечных колеса z1 и z4 и одно водило Н.
Ось вращения водила всегда совпадает с осями солнечных колес и называется центральной осью механизма.
Важно отметить, что в любом эпициклическом механизме никаких других звеньев (кроме сателлитов, солнечных колес и водил) не может быть. А если такие звенья все же имеются (рис. 7.7, б), то они не входят в состав эпициклического механизма, а образуют между собой кинематическую цепь, которая соединена с эпициклическим механизмом.
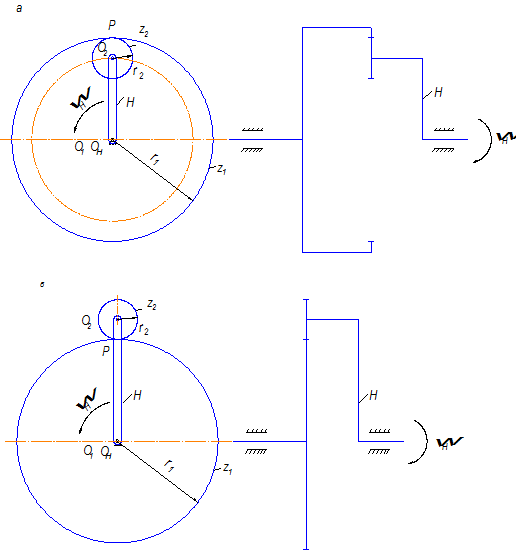
Рис. 7.6
Эпициклические механизмы делятся на планетарные и дифференциальные.
Планетарным называется эпициклический механизм, имеющий степень подвижности, равную единице.
Если степень подвижности эпициклического механизма больше единицы, то такой механизм называется дифференциальным или просто дифференциалом.
Подсчитаем число степеней подвижности эпициклического механизма, изображенного на рис. 7.7, а, в предположении, что центровые колеса подвижны
Рис. 7.7
Значит, этот механизм является дифференциальным. Если в этом механизме закрепить солнечное колесо z1, то он превратится в планетарный, так как будет обладать степенью подвижности, равной единице:
Подсчитаем теперь степень подвижности механизма, изображенного на рис. 7.7, б
Этот механизм является тоже дифференциальным, и если закрепить одно из солнечных колес (например, z1), то этот механизм превратится в планетарный, так как будет обладать степенью подвижности, равной единице:
Если же в механизмах (рис.7.7, а, б) остановить водило Н, то механизмы превратятся в простые зубчатые ряды.
Планетарные механизмы имеют степень подвижности, равную единице, поэтому они представляют собой в этом смысле обычные зубчатые механизмы с одним ведущим и одним ведомым звеном. Планетарные механизмы могут воспроизводить очень большие (или очень малые) передаточные отношения при малых габаритах и малом количестве зубчатых колес.
Наибольшее распространение имеют четырехколесные эпициклические механизмы. Если за основной механизм принять механизм, изображенный на рис. 7.7, а, то заменой одного или двух колес колесами с внутренним зацеплением можно будет получить другие механизмы.
Рассмотрим простейшие трехзвенные планетарные механизмы с внутренним (рис. 7.8, а) и внешним (рис. 7.8, б) зацеплением, у которых колеса 1 являются опорными.
Рис. 7.8
При вращении звена Н с угловой скоростью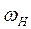 
колесо 2 обегает неподвижное колесо 1, вращаясь с угловой скоростью 
вокруг мгновенного центра вращения Р.
Для схемы с внутренним зацеплением (рис. 7.8, а) связь между угловыми скоростям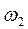и 
и 
может быть установлена из рассмотрения скорости точки О2, являющейся общей для колеса 2 и водила Н:
,
где знак «минус» при 
указывает на различие направлений вращения колеса 2 и водила Н
Тогда 
(7.9)
Отношение 
есть отношение механизма в предположении, что водило неподвижно.
Поэтому выражение (7.9) можно переписать в виде
(7.10)
или 
Для схемы с внешним зацеплением (рис. 7.8, б)
Тогда 
Если принять во внимание, что зацепление внешнее, то последнее выражение можно представить как
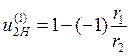(7.11)
Рассуждая аналогичным образом, можно получить формулу (7.10) для четырехзвенного механизма
(7.12)
Таким образом, если остановить поочередно одно из центральных колес и водило, то сумма этих передаточных отношений всегда равна единице.
Формула Виллиса. Если в четырехзвенном эпициклическом механизме оба центральных колеса подвижны, то такой механизм, как уже отмечалось выше, называется дифференциальным. Связь между угловыми скоростями солнечных колес удобно определять формулой Виллиса, для получения которой используется метод обращения движения, суть которого состоит в следующем.
Пусть звенья механизма, входящие в кинематические пары со стойкой, движутся с угловыми скоростями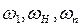 
. Относительное движение звеньев не изменится, если всем звеньям механизма сообщить дополнительное вращение с какой - либо общей угловой скоростью. Сообщим всем звеньям механизма дополнительное вращение вокруг оси ОН с угловой скоростью 
, равной по величине, но противоположной угловой скорости звена Н. Тогда звено Н останавливается и будет иметь место передача с неподвижными осями, для которой справедливо отношение
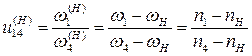(7.13)
где -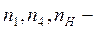 
частоты вращения колес 1, 4 и водила Н соответственно.
7.4 Синтез планетарных механизмов
В передачах с неподвижными осями при определении числа зубьев колес достаточно иметь в виду, что число зубьев ни одного зубчатого колеса не должно быть меньше предельного значения и при реализации заданного передаточного отношения механизм не должен выходить за допустимые габаритные размеры. Чтобы износ был равномернее, стараются отношение числа зубьев двух совместно работающих колес выбрать как нецелое число. Тогда одна и та же пара зубьев будет стираться только через продолжительное время.
В эпициклических передачах для увеличения жесткости и прочности, а также улучшения динамических свойств, планетарные редукторы выполнены не с одним, а с несколькими сателлитами. Поэтому встает вопрос о максимальном числе сателлитов. Кроме того, соосность центральных колес и водила для них обязательна.
В связи с этим, при проектировании эпициклических передач должны соблюдаться условия соосности, соседства и сборки.
Условие соосности.
Если ось вращения водила Н (рис. 7.9) геометрически совпадает с осями вращения солнечных колес 
и 
, то такой механизм называется соосным.
Условием соосности для механизма, изображенного на рис. 7.9, является равенство расстояний между осями первого и второго, третьего и четвертого колеса: 
или
(7.14)
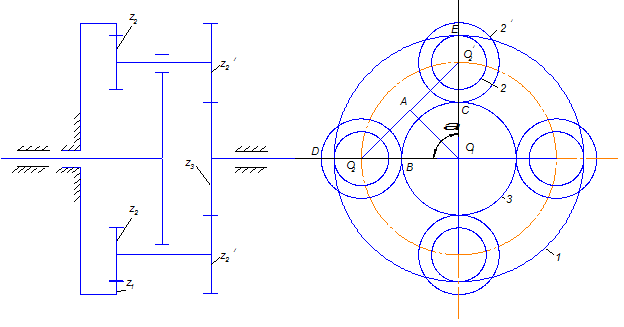
Рис. 7.9
Умножив уравнение (7.14) на два, получим
.
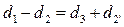Выразим диаметры через модуль:
или
.
Очень часто в эпициклических механизмах модули всех зубчатых колес бывают одинаковые. Тогда после сокращений на модуль условие соосности примет вид
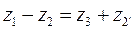(7.15)
Если сравнить уравнения (7.15) и (7.14), то можно заметить, что условие соосности, выраженное через радиусы колес или через числа зубьев колес, имеет одинаковый вид.
При синтезе эпициклических механизмов условия соосности приходится учитывать.
Условие соседства.
Условие, при котором сателлиты не будут задевать друг за друга, называется условием соседства.
Пусть имеем планетарный механизм, изображенный на рис. 7.9.
Максимальное число сателлитов, которое можно установить между солнечными колесами 
и 
, определяется условием отсутствия касания окружности вершин зубьев двух соседних сателлитов:
(7.16)
Из треугольника 
следует, что
.
Межосевое расстояние
.
Обозначим число сателлитов через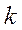 
, тогда угол
.
Радиус окружности вершин зубьев сателлитов
.
Подставив все эти значения в формулу (7.16), получим
.
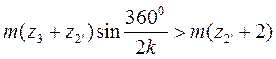После сокращения на модуль найдем
откуда
(7.17)
Это и есть условие соседства.
Условие сборки.
Число сателлитов, кроме того, должно удовлетворять условию сборки, которое заключается в том, что при установке первого сателлита солнечные колеса займут вполне определенные положения. Зубья следующих сателлитов могут не совпасть с впадинами одного из солнечных колес, и дальнейшая сборка будет невозможна.
Обратимся опять к рисунку 7.9. Сателлит BD касается солнечных колес в точках В и D, а соседний сателлит СЕ - в точках С и Е. Дуги ВС и DЕ являются дугами начальных окружностей колес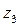 
и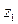 
.
Предположим, что на дуге ВС шаг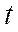 
уложился целое число раз 
и еще остался остаток, равный 
, тогда
.
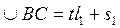Аналогично можно записать и для дуги DЕ:
.
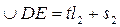Выразим дуги ВС и DЕ через число зубьев:
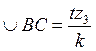и 
где 
- число сателлитов.
Возьмем сумму этих дуг
,
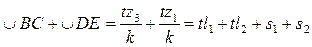откуда
(7.18)
Так как 
есть целое число, то и правая часть выражения (7.18) должна быть целым числом. Это возможно, если 
, так как каждый из отрезков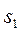 
и 
порознь меньше 
. Подставив в выражение (7.18)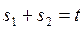 
, получим
или
,
где 
- целое число:
. (7.19)
Это и есть условие сборки, которое можно сформулировать так: сумма зубьев солнечных колес должна быть кратной числу сателлитов.
Рассмотрим пример.
Пусть дана структурная схема сложного зубчатого механизма, показанная на рис. 7.10.
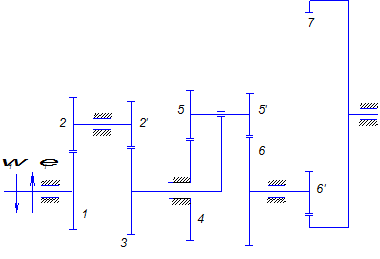
Рис. 7.10
Необходимо спроектировать кинематическую схему сложного зубчатого механизма.
Решение.
1. Выделим из состава сложного зубчатого механизма планетарный механизм (рис. 7.11).
Рис. 7.11
Заданная схема четырехколесного механизма имеет два сателлита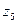 
и 
, два солнечных колеса z4 и z6 и водило Н.
2. Из условия соосности определяем число зубьев .
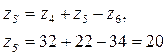
3. Определяем число сателлитных блоков для планетарной передачи. Условие, при котором сателлиты не будут задевать друг за друга, называется условием соседства (рис. 7.12).
Максимальное число сателлитов определяется условием отсутствия касания окружности вершин зубьев двух соседних сателлитов:
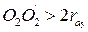
Рис. 7.12
Из треугольника 
следует, что
; 
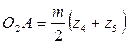
Обозначим число сателлитов через 
, тогда угол 
Радиус окружности вершин зубьев сателлитов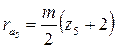 
Получим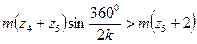 
После сокращения на модуль, найдем 
Откуда
Следовательно, 
Минимальное число сателлитов при этих условиях равно 6.
Условие сборки: k должно удовлетворять условию сборки, которое заключается в том, что при установке одного сателлита остальные займут строго определенные положения. Поэтому зубья следующих сателлитов могут не совпасть с впадинами одного из солнечных колес и дальнейшая сборка будет невозможна.
Для того, чтобы обеспечить условие сборки, необходимо и достаточно, чтобы сумма солнечных колес была кратна числу сателлитов.
.
Условие сборки выполняется.
4. Найдем передаточное число планетарной передачи:
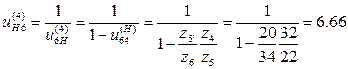
Передаточное число всего механизма
5. Определяем угловую скорость ведомого звена 7
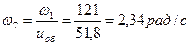
Определяем угловое ускорение ведомого звена 7
7. Определяем скорости точек начальных окружностей ведущего и ведомого колес
Определяем ускорения точек начальных окружностей ведущего и ведомого колес
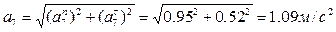
8. Определяем делительные диаметры колес
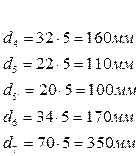
8. Вычерчиваем кинематическую схему планетарного редуктора (рис. 7.13).
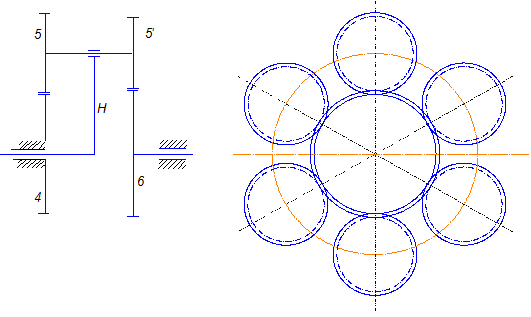
Рис. 7.13
СПИСОК ЛИТЕРАТУРЫ
1. Артоболевский И.И. Теория механизмов и машин. – М.: Наука, 1988. – 638 с.
2. Левитский Н.И. Теория механизмов и машин: Учеб. пособие для вузов. – 2-е изд., перераб. и доп. – М.: Наука, Гл. ред. физ.-мат. лит., 1990. – 592 с.
3. Озол О.Г. Теория механизмов и машин. – М.: Наука, 1984. – 432 с.
4. Попов С.А. Курсовое проектирование по теории механизмов и механике машин: Учеб. пособие для втузов / С.А. Попов, Г.А. Тимофеев; Под ред. К.В. Фролова. – 4-е изд., перераб. и доп. – М.: Высш. шк., 2002. – 411 с.
5. Теория механизмов и механика машин: Учеб. для втузов / К.В. Фролов, С.А. Попов, А.К. Мусатов и др.; Под ред. К.В. Фролова. – 3-е изд., стер. – М.: Высш. шк., 2001. – 496 с.
Учебное издание
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
