5.1 Общие понятия
Механизм, в состав которого входит вращающееся звено с рабочей поверхностью переменной кривизны, называемое кулачком, и выходное звено в виде толкателя (колебателя), образующих высшую кинематическую пару, называется кулачковым.
Классификация плоских кулачковых механизмов и основные параметры кулачка.
Плоские кулачковые механизмы (рис. 5.1) с вращающимся кулачком делятся на две группы: 1-ая группа преобразует вращательное движение кулачка в поступательное движение толкателя; 2-ая группа – вращательное движение кулачка в колебательное движение колебателя.
Рис. 5.1
Каждая из этих групп по форме элемента ведомого звена делится еще на три подгруппы, в которых кулачок работает: а) по острию; б) по ролику; в) по плоскости. Кулачковые механизмы, преобразующие вращательное движение в поступательное, у которых кулачок работает по острию или по ролику, в свою очередь делятся на центральные и дезаксиальные. Центральными называются такие, у которых ось толкателя проходит через центр вращения кулачка. В дезаксиальных же механизмах ось толкателя смещена относительно центра вращения кулачка на некоторую величину е, называемую дезаксиалом. Существует восемь основных схем кулачковых механизмов.
Профилем кулачка называется кривая, получаемая в сечении элемента кулачка плоскостью, перпендикулярной его оси вращения. Несмотря на большое разнообразие профилей кулачков, все они имеют некоторые общие параметры.
На рис. 5.2 показан кулачок, профиль которого вычерчен четырьмя дугами окружностей.
Рис. 5.2
Дуга ab проведена из центра О1, дуга bc - из центра О2, дуга cd - из центра О1, дуга da - из центра О2/. К основным размерам кулачка относятся следующие.
Минимальный радиус кулачка R0 - радиус, соединяющий центр вращения кулачка с ближайшей точкой профиля кулачка.
Максимальный радиус кулачка Rmax - радиус, соединяющий центр кулачка с самой удаленной точкой профиля кулачка.
Подъем толкателя h - разность длин максимального и минимального радиусов кулачка.
Нерабочий угол кулачка (нерабочая фаза) φ0 - центральный угол, опирающийся на дугу ab минимального радиуса. При скольжении по дуге минимального радиуса толкатель неподвижен и находится в нижнем положении.
Угол удаления (фаза удаления) φY - центральный угол кулачка, опирающийся на дугу bc, соединяющую крайние точки дуг минимального и максимального радиусов кулачка. При скольжении по дуге bc толкатель приходит в движение и удаляется на максимальное расстояние (переходит из нижнего в верхнее положение).
Угол дальнего стояния (фаза дальнего стояния) φд - центральный угол кулачка, опирающийся на дугу cd максимального радиуса. Пока толкатель скользит по дуге cd, он неподвижен и находится на максимальном расстоянии от центра вращения кулачка.
Угол возврата (фаза возврата) φB - центральный угол кулачка, опирающийся на дугу da, соединяющую крайние точки дуг максимального и минимального радиусов кулачка. При скольжении по дуге da толкатель возвращается из дальнего в исходное (нижнее) положение.
Рабочий угол кулачка (рабочая фаза) φP - центральный угол кулачка, равный сумме углов удаления, дальнего стояния и возврата 
.
Сумма всех углов должна быть равна 3600:
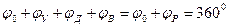
Радиусы профилей кулачка R2 (R2/) - радиусы дуг, соответствующие соответственно фазам удаления и возврата. Если кривая, соответствующая фазе удаления (или возврата), не является дугой окружности, то радиус профиля кулачка в этом случае будет переменный.
5.2 Анализ и синтез кулачковых механизмов
Задачей кинематического анализа является определение закона движения, скорости и ускорения толкателя (колебателя) по известным кинематической схеме механизма и частоте вращения кулачка.
Определение скоростей и ускорений толкателя (колебателя) находится графическим дифференцированием закона движения выходного звена.
Для анализа кулачковых механизмов с произвольным профилем кулачка применяют метод обращенного движения, при котором кулачок считается неподвижным, а стойке вместе с толкателем (колебателем) сообщается вращательное движение вокруг оси кулачка с угловой скоростью кулачка, но в противоположном направлении. В таком движении перемещение толкателя (колебателя) относительно кулачка будет таким же, как и в истинном движении при неподвижной стойке.
При синтезе находится профиль кулачка по известным структурной схеме, основным размерам кулачка и законе движения толкателя (колебателя).
5.2.1 Центральный кулачковый механизм, в котором кулачок работает по толкателю с острием
Анализ механизма.
Известны: параметры кинематической схемы механизма и частота вращения кулачка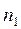 
(мин-1 ).
Для нахождения перемещения толкателя строится кинематическая схема механизма (рис. 5.3,а), например, в масштабе
, (5.1)
где 
- радиус минимальной окружности кулачка в м;
- радиус окружности на чертеже в мм.
Рис. 5.3
На окружности радиуса 
откладывается рабочий угол 
(на примере 
), который находится из выражения
(5.2)
где 
, 
- соответственно время одного оборота и рабочее время в с.
Время полного оборота кулачка
(5.3)
Рабочий угол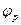 
делится на 
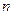равных частей (на рис. 5.3- на 18) и через центр О1 и точки 1-18 проводятся радиусы до встречи с профилем кулачка. Расстояния 1-1/, 2-2/, … от окружности минимального радиуса до профиля кулачка и есть перемещения толкателя, соответствующие повороту кулачка на угол, определяемый номером деления.
Для построения графической зависимости 
в системе координат 
в системе координат 
выбираются масштабы перемещения толкателя 
и времени 
; м/мм (5.4)
, с/мм (5.5)
где 
- ордината в мм, соответствующая перемещению толкателя в 
-том положении в м;
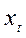-абсцисса в мм, соответствующая времени поворота кулачка на рабочий угол 
в с.
В том случае, когда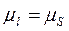 
, масштабы кинематической схемы и графика одинаковые. Ось абсцисс 
делится на 
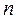равных частей (в данном случае на 18) и через точки деления проводят отрезки 1-1//, 2-2//,…,18-18//), выражающие в соответствующем масштабе соответствующие перемещения толкателя (рис. 5.3, б).
Синтез механизма.
Известны: структурная схема механизма, основной размер R0 и частота вращения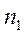 
кулачка, закон движения толкателя, заданный одним из кинематических графиков (рис. 5.4,а).
Необходимо построить профиль кулачка.
Пусть, как и в случае анализа 
, а закон движения 
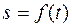представлен графиком 
.
а) б)
Рис. 5.4
Для решения поставленной задачи в масштабе 
(5.1) вычерчивается окружность радиуса R0 кулачка и на ней откладывается рабочий угол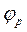 
, который делится на n равных частей. Через точки деления и центр окружности проводятся лучи. Абсцисса графика 
делится на такое же n число частей и на ординатах находят соответствующие им значения 
, которые в масштабе выражают соответствующие положения острия толкателя на профиле кулачка. Поэтому, если от окружности на лучах отложить, с учетом масштаба, отрезки 
и соединить эти точки плавной линией, получим профиль кулачка, обеспечивающий требуемый режим движения (рис. 5.4, б).
5.2.2 Дезаксиальный кулачковый механизм, в котором кулачок работает по толкателю с острием
Кинематический анализ механизма.
Пусть задана кинематическая схема механизма (рис. 5.5) в масштабе (5.1). Проводим окружность минимального радиуса и окружность дезаксиала (радиус которой равен дезаксиалу 
). Если бы вместо кулачка вращалась окружность минимального радиуса (вокруг того же центра О1), то толкатель был бы неподвижным, а его острие постоянно находилось бы в точке 6/ (и скользило бы по окружности минимального радиуса). На самом же деле вращается кулачок и в положении, изображенном на рис. 5.5, а, острие толкателя находится в точке 6//; следовательно, отрезок 6/-6// касательной к окружности дезаксиала, заключенный между окружностью минимального радиуса и профилем кулачка, является подъемом толкателя в данном положении. Чтобы найти подъемы толкателя в других положениях, нужно окружность дезаксиала разбить на части, через точки деления провести касательные и измерить соответствующие отрезки этих касательных. Но обычно деление начинают не с произвольной точки, а с точки, в которой начинается подъем толкателя. На рис. 5.5, а видно, что такой точкой на профиле кулачка является точка О/ (в которой профиль кулачка отделяется от окружности минимального радиуса). Нужно найти соответствующую точку на окружности дезаксиала. Для этого через точку О/ проводим касательную к окружности дезаксиала. Точка касания О и будет искомой точкой. От точки О на окружности дезаксиала откладываем рабочий угол 
(5.2) и делим его на несколько равных частей (на рис. 5.5, а рабочий угол разделен на 8 частей). Через точки деления проводим касательные к окружности дезаксиала. Отрезки касательных между окружностью минимального радиуса и профилем кулачка и будут искомые перемещения толкателя (рис. 5.5, б).
Можно было бы по этим перемещениям построить графики 
, воспользовавшись выражениями (5.4) и (5.5).
Рис. 5.5
Но, как видно, ни одна касательная не прошла через носок кулачка (точку 
), следовательно, на графике будет отсутствовать максимальный подъем толкателя. Чтобы исправить это положение, через носок кулачка проводим касательную к окружности дезаксиала и отмечаем точку касания 
.
Отложив найденные перемещения толкателя в масштабе (5.4) от оси абсцисс (рис. 5.5, б) получим график 
.
Несмотря на то, что кулачок был симметричным, график получился несимметричным (об асимметрии графика 
можно судить хотя бы по тому, что максимальный подъем толкателя получился не посередине графика). Это свойство дезаксиальных кулачковых механизмов используют на практике, когда хотят получить симметричный кулачок при асимметричном графике.
Синтез механизма.
Пусть теперь заданы график (рис. 5.5, б) и основные размеры кулачка (минимальный радиус кулачка 
, дезаксиал 
и рабочий угол кулачка 
). Требуется построить профиль кулачка.
Делим заданный график 
ординатами на несколько равных участков (на рис. 5.5, б график 
разделен на восемь участков). Если ни одна из ординат не прошла через точку 
, соответствующую максимальному подъему толкателя, то через эту точку проводим дополнительно ординату 
.
Выбираем масштаб (5.1), в котором должна быть вычерчена кинематическая схема механизма и из одного центра О1 (рис. 5.5, а) проводим две окружности: минимального радиуса и дезаксиала. На окружности дезаксиала от произвольной точки О откладываем рабочий угол 
(5.2) и делим его на столько равных частей, на сколько разбит график 
. Через точки деления 0, 1, 2 и т.д. проводим к окружности дезаксиала касательные. На этих касательных от окружности минимального радиуса откладываем перемещения толкателя, взятые из графика 
. Если масштабы длин на графике и кинематической схеме разные, то, воспользовавшись зависимостями (5.1) и (5.4), получим их в нужном масштабе. Соединив концы отложенных перемещений плавной кривой, получим искомый профиль кулачка (рис. 5.5, а). От оси вращений О1 кулачка на расстоянии дезаксиала 
вычерчиваем толкатель. Таким образом требуемая кинематическая схема кулачкового механизма готова.
5.2.3 Центральный кулачковый механизм, в котором кулачок работает по толкателю с роликом
Анализ механизма.
Пусть задана кинематическая схема центрального кулачкового механизма (рис. 5.6, а). Требуется произвести кинематический анализ, т. е. построить график .
Траектория центра ролика (точки В) при движении его относительно кулачка (в обращенном движении) называется центровым профилем кулачка. Так как центр ролика В находится от действительного профиля кулачка все время на одном и том же расстоянии, равном радиусу ролика 
, то центровой и действительный профили кулачка будут эквидистантными (равностоящими) кривыми.
|
Рис. 5.6
Построение эквидистантной кривой Э к данной кривой К показано на рис. 5.6, в. Пусть требуется к данной кривой К построить эквидистантную кривую Э на расстоянии, равном 
. Для этого на кривой К выбираем ряд точек (на расстоянии 3-5 мм друг от друга) и из этих точек проводим дуги радиусом, равным 
. Огибающая этих дуг Э и будет искомой эквидистантной кривой. В частном случае для окружности эквидистантной кривой будет окружность, концентрическая данной.
На схеме механизма (рис. 5.6, а) построим центровой профиль кулачка (на участке 
центрового профиля показано его построение по описанному выше способу).
Центровому профилю соответствует свой (увеличенный) минимальный радиус. Обозначим его через 
, тогда
, (5.6)
где 
- минимальный радиус кулачка;
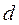- диаметр ролика.
Теперь заменим действительный кулачок, работающий по ролику, центровым, работающим по толкателю с острием (на рис. 5.6, а этот толкатель показан пунктиром). Кинематический анализ такой схемы изложен выше.
Синтез механизма.
Синтез производится в порядке, обратном анализу. Пусть заданы график (рис. 5.6, б) и основные размеры кулачка. Требуется построить профиль кулачка. Сначала строим центровой профиль кулачка, работающего по острию (при построении центрового профиля минимальный радиус 
принимается равным 
).
Затем от центрового профиля переходим к действительному, построив эквидистантную кривую «внутрь». На участке 
действительного профиля (рис. 5.6, а) показано его построение (как эквидистантной кривой).
5.2.4 Дезаксиальный кулачковый механизм, в котором кулачок перемещает толкатель с роликом
Анализ механизма.
Пусть задана кинематическая схема дезаксиального кулачкового механизма с роликом (рис. 5.7). Требуется произвести кинематический анализ.
Действительный кулачок (работающий по ролику) заменяем центровым профилем, работающим по толкателю с острием (на участке 
центрового профиля показано его построение как эквидистантной кривой к действительному профилю кулачка). Затем производится кинематический анализ центрового профиля кулачка, работающего по толкателю с острием.
|
Рис. 5.7
Синтез механизма.
Синтез производится в порядке, обратном анализу. Сначала по заданному графику находят центровой профиль кулачка (при построении центрового профиля минимальный радиус кулачка увеличивается на величину радиуса ролика 
).
Затем от центрового профиля переходят к действительному, построив эквидистантную кривую внутрь (рис. 5.7). На участке 
действительного профиля показано его построение (как эквидистантной кривой).
5.2.5 Кулачковый механизм, в котором кулачок перемещает плоский толкатель
Анализ механизма.
Пусть задана кинематическая схема кулачкового механизма с плоским толкателем (рис. 5.8, а). Требуется произвести кинематический анализ, т. е. построить график 
Проводим в масштабе (5.1) окружность минимального радиуса 
, отложим на этой окружности рабочий угол 
и разделим его на 12 равных частей. Применим метод обращенного движения. Пусть в обращенном движении ось толкателя О1В повернулась на 300 и заняла первое положение О1В1. Нужно найти положение тарелки толкателя 
, которая во время работы постоянно касается профиля кулачка и остается перпендикулярной к оси толкателя. Поводим касательную 
к профилю кулачка, которая одновременно является перпендикуляром к оси О1В1 толкателя в первом положении. Расстояние 1-с1 от окружности минимального радиуса до тарелки толкателя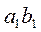 
и будет перемещением толкателя в первом положении. Таким же путем найдем перемещение 2-с2 во втором положении и во всех последующих (перемещения толкателя на рис. 5.8, а показаны жирными линиями). Отложив найденные перемещения от оси абсцисс (рис. 5.8, б), получим график 
.
|
|
Рис. 5.8
Синтез механизма.
Синтез проводится в порядке, обратном анализу. Пусть теперь задан график (рис.5.8, б); требуется построить профиль кулачка, работающего по плоскому толкателю. Проводим окружность минимального радиуса (рис. 5.8, а). От произвольной точки О этой окружности откладываем заданный рабочий угол 
и разбиваем его на 12 равных частей. По графику находим перемещения толкателя, соответствующие каждому положению оси его в обращенном движении (разбивая график на столько же равных частей, на сколько разбит рабочий угол кулачка). От окружности минимального радиуса на продолжении радиусов откладываем соответствующие перемещения, взятые из графика , получим точки с1, с2, с3, …, с12 (если масштабы длин на графике и кинематической схеме различные, то прежде чем откладывать перемещения толкателя, необходимо воспользоваться формулой (5.5). Через точки с1, с2, с3 и т. д. проводим перпендикуляры 
, 
, 
, … к продолжениям радиусов и найдем, таким образом, 12 положений тарелки 
.
Действительным профилем кулачка будет огибающая всех положений тарелки толкателя. Для того, чтобы профиль кулачка получить более точным, необходимо найти возможно большее количество положений тарелки толкателя в обращенном движении.
5.2.6 Кулачковый механизм, в котором кулачок перемещает коромысло с острием
Анализ механизма.
Пусть задана кинематическая схема кулачкового механизма с колебателем (рис. 5.9, а). Требуется произвести кинематический анализ, т. е. построить график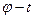 
. Центр вращения колебателя О в обращенном движении будет двигаться по окружности радиуса О1О (рис. 5.9, а).
На этой окружности от точки О отложим в сторону, противоположную угловой скорости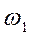 
кулачка, рабочий угол кулачка 
и разобьем его на 12 равных частей. На рис. 5.9, а колебатель ОВ показан в нижнем положении (в начале подъема). Если на кинематической схеме колебатель будет изображен не в нижнем положении, а в промежуточном, то предварительно нужно найти положение центра вращения колебателя, соответствующее началу подъема в обращенном движении (на окружность радиуса О1О), и от этой точки откладывать рабочий угол 
. В обращенном движении центр вращения О колебателя на окружности радиуса О1О занимает последовательные положения 1, 2, 3, …, 12 (соответствующие повороту кулачка на один и тот же угол). Второй конец колебателя (точка В) скользит по профилю кулачка. Находим последовательные положения точки В. Для этого длиною колебателя ОВ из точек 1, 2, 3, …, 12 (окружности радиуса О1О) делаем засечки на профиле кулачка, получим точки 1/, 2/, 3/, …, 12/.
В истинном движении конец колебателя В будет двигаться по дуге 
, описанной радиусом ОВ из центра О. Чтобы найти соответствующие положения точки В в истинном движении, нужно на дуге 
сделать засечки из центра вращения О1 кулачка расстояниями О11/, О12/, О13/, …, О112/, получим точки 1//, 2//, 3//, …, 12//. При построении графика 
можно вместо углов поворота колебателя откладывать длины дуг В-1//, В-2// и т. д., измеренные непосредственно по дуге 
. Масштабный коэффициент угла поворота 
колебателя в этом случае
,рад/мм, (5.7)
где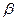 
- угол размаха колебателя, град;
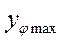- максимальная ордината на графике 
, мм.
а) б)
|
Рис. 5.9
Синтез механизма.
Синтез производится в порядке, обратном анализу. Пусть теперь будут заданы график 
(рис. 5.9, б), минимальный радиус кулачка 
и длина колебателя ОВ. Требуется построить профиль кулачка.
Из произвольной точки О1 описываем окружность минимального радиуса 
(рис. 5.9, а). На этой окружности в произвольном месте выбираем точку В (соответствующую началу поворота колебателя). От точки В в заданном направлении (а если направление не задано, то в произвольном направлении) откладываем длину колебателя ВО. Затем из центра О1 описываем окружность радиусом О1О. Если задано межосевое расстояние О1О, а не длина колебателя ВО, то сразу описывается окружность этим радиусом и на ней выбирается произвольная точка О, соответствующая положению колебателя в начале подъема. На этой окружности от точки О отложим (в сторону, противоположную угловой скорости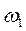 
кулачка) рабочий угол 
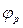и разобьем его на несколько равных частей. Затем из центра О радиусом ОВ проводим дугу 
и откладываем на ней (в нужном масштабе) угловые перемещения колебателя, взятые из заданного графика 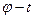. Точки, принадлежащие профилю кулачка, получаем засечками.
Для этого из центра О1 радиусами, равными расстояниям О11//, О12//, О13// и т. д., проводим дуги, на которых делаем засечки длиной колебателя ОВ из точек 1, 2, 3, …, 12, лежащих на окружности радиуса О1О. Соединив точки 1/, 2/, 3/, …, 12/ (пересечения дуг) плавной кривой, получим действительный профиль кулачка.
5.2.7 Кулачковый механизм, в котором кулачок перемещает коромысло с роликом
Анализ механизма.
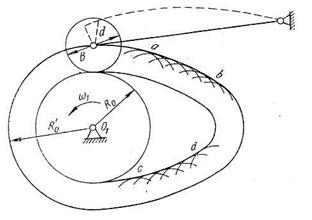
Пусть задана кинематическая схема кулачкового механизма с роликовым колебателем (рис. 5.10). Требуется произвести кинематический анализ. Действительный кулачок, работающий по ролику, заменяем центровым профилем, работающим по колебателю с острием (на участке 
центрового профиля показано его построение как эквидистантной кривой). Затем производим кинематический анализ центрового профиля кулачка, работающего по колебателю с острием (на рис. 5.10 такой колебатель показан пунктиром).
|
Рис. 5.10
Синтез механизма.
Синтез производится в порядке, обратном анализу. Сначала по заданному графику 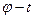находят центровой профиль кулачка (при построении центрового профиля минимальный радиус кулачка увеличивают на величину радиуса ролика 
).
Затем от центрового профиля переходят к действительному, построив эквидистантную кривую внутрь (на участке 
действительного профиля показано его построение как эквидистантной кривой).
5.2.8 Кулачковый механизм, в котором кулачок работает по плоскому колебателю
Анализ механизма.
Пусть задана кинематическая схема кулачкового механизма с плоским колебателем (рис. 5.11, а). Требуется произвести кинематический анализ, т. е. построить график 
.
Центр вращения О колебателя в обращенном движении будет двигаться по окружности радиуса О1О (рис. 5.11, а). На этой окружности от точки О, соответствующей нижнему положению (началу подъема) колебателя, отложим в сторону, противоположную угловой скорости 
кулачка, рабочий угол 
и разобьем его на 12 равных частей. В обращенном движении центр вращения О колебателя занимает на окружности О1О последовательные положения, обозначенные 1, 2, 3, …, 12, соответствующие повороту кулачка на один и тот же угол (на 300).
Проведя из точек 1, 2, 3 и т. д. (окружности радиуса О1О) касательные к профилю кулачка, найдем последовательные положения колебателя в обращенном движении, соответствующие повороту кулачка на один и тот же угол. Отложив на этих касательных длину колебателя ОА, получим точки 1/, 2/, 3/, …, представляющие собой последовательные положения свободного конца А колебателя в обращенном движении. Если ни одно из положений колебателя не касается самой удаленной точки профиля кулачка, то через эту точку проводим дополнительную касательную 
, (рис. 5.11, а), соответствующую максимальному повороту колебателя.
В истинном движении при повороте колебателя его свободный конец (точка А) движется по дуге окружности радиуса ОА. Для того, чтобы на дуге найти последовательные положения свободного конца колебателя, нужно из центра вращения О1 кулачка сделать засечки расстояниями, равными О11/, О12/, О13/, …; получим точки 1//, 2//, 3//, … Если эти точки соединить с центром вращения О колебателя, то получим последовательные положения колебателя, соответствующие повороту кулачка на один и тот же угол (на 300).
На рис. 5.11, б изображен график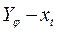 
. Ординаты этого графика равны длинам дуг 
, 
, 
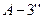, … Масштабный коэффициент 
угла поворота колебателя определяется по формуле (5.7).
Синтез механизма.
Синтез проводится в порядке, обратном анализу. Пусть теперь заданы кинематический график 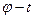(рис. 5.11, б), минимальный радиус кулачка 
, межосевое расстояние О1О и рабочий угол 
кулачка 
. Требуется построить профиль кулачка.
Из произвольной точки О1- центра вращения кулачка- описываем две окружности радиусами, равными минимальному радиусу 
и межосевому расстоянию О1О (рис. 5.11, а). На окружности радиуса О1О выбираем в произвольном месте центр вращения колебателя О, откладываем от него (в сторону, обратную угловой скорости 
кулачка) рабочий угол 
кулачка и разбиваем его на 12 равных частей. Из точки О проводим касательную к окружности минимального радиуса 
; это и будет нижнее положение колебателя. Длину колебателя ОА принимаем произвольной. Свободный конец колебателя А будет двигаться по дуге , описанной из центра О радиусом, равным длине колебателя ОА. На этой дуге от точки А откладываем (в нужном масштабе) угловые перемещения конца колебателя, взятые из заданного графика 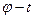, и получаем точки 
, 
, 
, …
|
Рис. 5.11
В обращенном движении один конец колебателя (центр вращения О) перемещается по окружности радиуса О1О и занимает последовательные положения 1, 2, 3,... Последовательные положения другого (свободного) конца колебателя в обращенном движении найдем засечками. Для этого через точки , , , …, лежащие на дуге , проводим дуги (из центра О1), на которых длиной колебателя ОА делаем засечки из соответствующих точек 1, 2, 3, …, лежащих на окружности радиуса О1О; в пересечении получим точки 
, 
, 
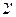, …, представляющие собой последовательные положения свободного конца А колебателя в обращенном движении. Соединив точки 1 и 
, получим первое положение колебателя, соединив точки 2 и 
- второе положение колебателя и т. д. Действительным профилем кулачка будет огибающая всех положений колебателя.
Для того, чтобы профиль кулачка получился более точным, необходимо найти возможно большее количество положений колебателя.
