Министерство образования Республики Беларусь
Учреждение образования
Гомельский государственный университет
имени Франциска Скорины»
В.В. БУРАКОВСКИЙ, Т.В. БОРОДИЧ
ОСНОВЫ ВЫСШЕЙ МАТЕМАТИКИ
для студентов исторического факультета,
факультета иностранный язык
Тексты лекций
Гомель 2011
УДК 512 (078)
ББК 22.14 Я73
Х 69
Рецензенты:
Рекомендованы к изданию научно-методическим советом учреждения образования «Гомельский государственный университет имени Франциска Скорины»
Бураковский В.В.
Х 69 Основы высшая математика. /Бураковский В.В., Бородич Т.В. − Гомель: УО «ГГУ им. Ф.Скорины», 2011. − 34с.
Краткое изложение курса лекций по основам высшей математике студентам специальностей:
© В.В. Бураковский, Т.В. Бородич 2011
© Учреждение образования «Гомельский государственный университет имени Франциска Скорины», 2011
СОДЕРЖАНИЕ
| Введение………………………………………………………...... | |
| 1 Элементы теории множеств. Множества и операции над ними………………………………..…………………................... | |
| 2 Функции и способ их задания….…………………................... | |
| 3 Предмет и задачи теории вероятности. События и операции над ними. Относительные частоты и их свойства …………….. | |
| 4 Аксиомы теории вероятности. Дискретные пространства элементарных исходов. Классическое определение вероятности ……………………………………………………................... | |
| 5 Основные правила комбинаторики. Выборки, сочетания. Аксиомы теории вероятности …………………………................... | |
| 6 Геометрические вероятности ………………………................ | |
| 7 Свойства вероятности……………………………..................... | |
| 8 Условная вероятность. Независимость ……………................ | |
| 9 Формулы полной вероятности и Байеса.................................. | |
| 10 Схема независимых испытаний Бернулли. Полиноминальное распределение ………………………………………………. | |
| 11 Теорема Пуассона. Локальная и интегральная теоремы Муавра-Лапласа …………………………………….................... | |
| 12 Случайные величины ………………………………………... | |
| 13 Дискретные случайные величины ……………….................. | |
| 14 Числовые характеристики дискретных случайных величины…………………………............................................................. | |
| 15 Непрерывные случайные величины ………………............... | |
| Литература………………………………………………………... |
Введение
Тексты лекций по учебному курсу ”Основы высшей математики”, предназначенный для обучения студентов факультета иностранных языков, исторического факультета. Тексты лекций написаны в соответствии с действующей программой по данному предмету.
Основное направление текстов лекций – теория вероятностей. В них рассмотрены следующие темы: классическое определение вероятности, основные формулы комбинаторики, геометрические вероятности, теоремы сложения и умножения вероятностей, формулы полной вероятности и Байеса, формула Бернулли, законы распределения и числовые характеристики случайных величин. Содержит основные теоретические сведения, примеры решения задач по теории вероятностей и контрольные задания. Предназначен для студентов математического, физического, экономического и заочного факультетов.
Элементы теории множеств. Множества и операции над ними
Понятие множества является одним из основных математических понятий. Это неопределяемое понятие, его можно только описать или пояснить на примерах. Так, можно говорить о множестве букв в латинском алфавите, множество всех книг в данной библиотеке, множестве студентов в данной группе, множестве всех точек данной линии. Чтобы задать множество, достаточно перечислить элементы или указать характеристические свойства элементов, т.е. такое свойство, которым обладают все элементы данного множества и только они.
Определение 1.1. Предметы (объекты), составляющие некоторое множество, называются его элементами.
Множество принято обозначать прописными латинскими буквами, а элементы множества – строчными буквами. То, что x является элементом множества A, записывается так: x 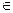 A (x принадлежит A). Запись вида x
A (x принадлежит A). Запись вида x 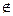 A (x
A (x  A) означает, что x не принадлежит A, т.е. не является элементом множества A.
A) означает, что x не принадлежит A, т.е. не является элементом множества A.
Элементы множества принято записывать в фигурных скобках. Например, если A – множество, состоящее из первых трех букв латинского алфавита, то его записывают так: A= { a,b,c }.
Множество может содержать бесконечно много элементов (множество точек прямой, множество натуральных чисел), конечное число элементов (множество школьников в классе), либо вообще не содержать ни одного элемента (множество студентов пустой аудитории).
 Определение 1.2. Множество, не содержащее ни одного элемента, называется пустым множеством, обозначается Ø.
Определение 1.2. Множество, не содержащее ни одного элемента, называется пустым множеством, обозначается Ø.
Определение 1.3. Множество A называется подмноже-ством множества B, если каждый элемент множества A принадлежит и множеству B. Это обозначается A  B (A – подмножество B).
B (A – подмножество B).
Пустое множество считают подмножеством любого множества. Если множество A не является подмножеством множества B, то пишут A  B.
B.
 Определение 1.4. Два множества A и B называют равными, если являются подмножествами друг друга. Обозначают A = B. Это означает, что если x
Определение 1.4. Два множества A и B называют равными, если являются подмножествами друг друга. Обозначают A = B. Это означает, что если x 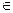 A, то x
A, то x 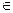 B и наоборот, т.е. если
B и наоборот, т.е. если  и
и  , то
, то  .
.
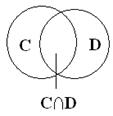
Определение 1.5. Пересечение множеств A и B называют множество M, элементы которого являются одновременно элементами обоих множеств A и B. Обозначают M= A 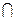 B. Т.е. x
B. Т.е. x 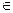 A
A 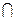 B, то x
B, то x 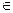 A и x
A и x 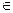 B.
B.
Записывают A 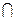 B= { x | x
B= { x | x 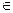 A и x
A и x 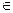 B }. (Вместо союза и – ставятся знаки
B }. (Вместо союза и – ставятся знаки 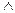 , &).
, &).
 Определение 1.6. Если A
Определение 1.6. Если A 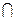 B= Ø, то говорят, что множества A и B не пересекаются.
B= Ø, то говорят, что множества A и B не пересекаются.
Аналогично можно определить пересечение 3-х, 4-х и любого конечного числа множеств.
 Определение 1.7. Объединением множеств A и B называют множество M, элементы которого принадлежат хотя бы одному из данных множеств.Обозначают M=A
Определение 1.7. Объединением множеств A и B называют множество M, элементы которого принадлежат хотя бы одному из данных множеств.Обозначают M=A 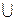 B. Т.о. A
B. Т.о. A 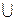 B= { x | x
B= { x | x 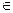 A или x
A или x 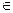 B }. (Вместо союза или – ставится знак
B }. (Вместо союза или – ставится знак 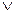 ).
).
Аналогично определяется и множество A1 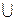 A2
A2 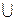 …
… 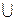 An. Оно состоит из элементов, каждый из которых принадлежит хотя бы одному из множеств A1, A2,…, An (а может быть, и нескольким сразу).
An. Оно состоит из элементов, каждый из которых принадлежит хотя бы одному из множеств A1, A2,…, An (а может быть, и нескольким сразу).
Пример 1.8. 1) если A= {1;2;3;4;5} и B= {1;3;5;7;9}, то A 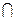 B= {1;3;5} и A
B= {1;3;5} и A 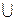 B= {1;2;3;4;5;7;9}.
B= {1;2;3;4;5;7;9}.
2) если A= {2;4} и B= {3;7}, то A 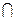 B= Ø и A
B= Ø и A 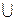 B= {2;3;4;7}.
B= {2;3;4;7}.
3) если A= {летние месяцы} и B= {месяцы, в которых 30 дней}, то A 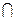 B= {июнь} и A
B= {июнь} и A 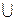 B= {апрель; июнь; июль; август; сентябрь; ноябрь}.
B= {апрель; июнь; июль; август; сентябрь; ноябрь}.
Определение 1.9. Натуральными называются числа 1,2,3,4,…, используемые для счета предметов.
Множество натуральных чисел обозначается N, N={1;2;3;4;…;n;…}. Оно является бесконечным, имеет наименьший элемент 1 и не имеет наибольшего элемента.
Пример 1.10. A – множество натуральных делителей числа 40. Перечислить элементы этого множества. Верно ли, что 5 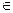 A, 10
A, 10 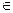 A, -8
A, -8 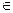 A, 4
A, 4 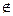 A, 0
A, 0 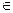 A, 0
A, 0 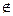 A.
A.
 A = {1,2,4,5,8,10,20,40}. (В,В,Н,Н,Н,В)
A = {1,2,4,5,8,10,20,40}. (В,В,Н,Н,Н,В) 
Пример 1.11. Перечислите элементы множеств, заданных характеристическими свойствами:
а) А ={ x | (x -1)(2 x -1)(3+ x)=0}, получаем A = {1; 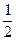 ;-3}
;-3}
б) B ={ x | -1,1< x < 5 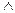 x
x 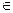 N}, имеем B = {1;2;3;4}.
N}, имеем B = {1;2;3;4}.
Пример 1.12. Дано множество чисел K = {21;54;153;171;234}. Составить подмножество чисел из K, которые а) делятся на 7; б) делятся на 9; в) не делятся на 5; г) делятся на 4.
 а) A = {21}, б) B = {54;153;171;234}, в) C = K, г) D= Ø
а) A = {21}, б) B = {54;153;171;234}, в) C = K, г) D= Ø 
Пример 1.13. Множество C состоит из 11 элементов, множество D – из 8. Сколько элементов содержит C 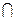 D, если C
D, если C 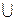 D содержит 15 элементов?
D содержит 15 элементов?
 Поскольку A+B –A
Поскольку A+B –A 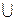 B=A
B=A 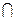 B, тогда 11+8–15=4
B, тогда 11+8–15=4 
 Определение 1.14. Разность множеств A и B называется множество M, элементы которого принадлежат множеству A и не принадлежат множеству B.
Определение 1.14. Разность множеств A и B называется множество M, элементы которого принадлежат множеству A и не принадлежат множеству B.
Обозначают M=A \ B.
Таким образом, A \ B= { x | x 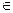 A и x
A и x 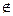 B }.
B }.
Пример 1.15. Если A = {1;2;3;4;5} и B = {1;5}, то A\B= {2;3;4}.






