Использование индексного метода в анализе взаимосвязи экономических явлений

 

Индексный метод используется при изучении роли отдельных факторов в динамике какого – либо сложного явления, позволяя определить размер абсолютного изменения сложного явления за счет каждого фактора в отдельности.

Роль отдельных факторов результативного показателя оценивается путем построения системы взаимосвязанных индексов. В основе приема аналитических индексных расчетов лежит принцип элиминирования изменений величины всех факторов, кроме изучаемого. Предпосылкой такого анализа является возможность представления результативного экономического показателя произведением двух или более определяющих его величину показателей (факторов) или суммой таких произведений.

Предположим, что сложный результативный показатель А = а* b, где а и b – показатели- факторы.

Изменение сложного явления может быть представлено индексом:

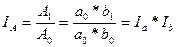. (8.45)

Абсолютное изменение явления А под влиянием всех факторов представляет собой разность между числителем и знаменателем индекса:

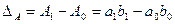. (8.46)

Для выявления каждого фактора в отдельности индекс сложного показателя разлагают на частные (факторные) индексы, характеризующие роль каждого.

Применяются два метода разложения общего индекса на частные:

- метод обособленного изучения факторов;

- метод последовательно – цепной.

Сущность метода обособленного изучения факторов заключается в том, что при выявлении влияния отдельного фактора сложный показатель берется в том виде, какой бы он имел, если бы изменился лишь один данный фактор, а все прочие остались неизменными на уровне базисного периода. Роль каждого фактора определяется по следующим формулам:

фактор а: 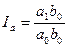; (8.47)

фактор b: 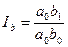. (8.48)

Абсолютное изменение результативного показателя за счет каждого фактора получается как разность между числителем и знаменателем индекса:

фактор а: 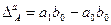; (8.49)

фактор b: . (8.50)

Однако необходимо иметь в виду, что факторные индексы при данном методе не разлагают полностью величины абсолютного изменения результативного показателя. Получается некоторый неразложенный остаток, который следует рассматривать как результат совместного действия факторов, т.е.

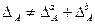. (8.51)

При последовательно-цепном методе используется система взаимосвязанных индексов, требующая правильного расположения факторов при написании модели результативного показателя (например, А = а * b * с). На первом месте в модели следует ставить качественный фактор. Увеличение цепи факторов на один фактор (например, a * b) каждый раз должно давать показатель, имеющий реальный экономический смысл. При выявлении влияния факторов определяются факторные индексы. При определении влияния первого фактора все остальные факторы сохраняются в числителе и знаменателе на уровне отчетного периода. При построении второго фактического индекса первый фактор сохраняется на уровне базисного периода, третий и все последующие – на уровне отчетного периода; при построении третьего факторного индекса первый и второй факторы сохраняются на уровне базисного периода, четвертый и все последующие – на уровне отчетного периода и т.д.

Предположим, что A = a * b * c, при этом обеспечена правильность расположения факторов:

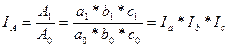. (8.52)

Частные индексы следующие:

фактора а ; (8.53)

фактора 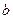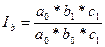; (8.54)

фактора с 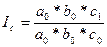. (8.55)

Абсолютное изменение результативного показателя за счет каждого фактора:

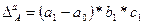; (8.56)

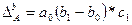; (8.57)

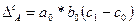; (8.58)

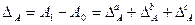. (8.59)

Абсолютное изменение сложного экономического показателя за счет каждого фактора может быть определено и в том случае, если этот показатель представляет собой сумму произведений, определяющих его величину показателей. К числу таких показателей относятся: общая стоимость всей выработанной (или реализованной) продукции, общая сумма затрат на ее производство, общая сумма затрат труда на производство всей продукции.

Агрегатный индекс общей стоимости продукции (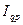) равен произведению агрегатного индекса физического объема продукции (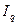) и агрегатного индекса цен (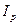), если коэффициент соизмерения в индексе физического объема взяты из базисного периода, а веса в индексе цен – из текущего периода. В общем виде это равенство должно быть записано так:

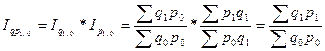. (8.60)

Общее абсолютное изменение общей стоимости продукции за счет двух факторов составляет:

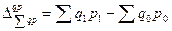. (8.61)

Абсолютное изменение общей стоимости продукции за счет отдельных факторов:

а) изменения физического объема продукции

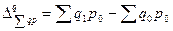. (8.62)

б) среднего изменения цен на продукцию

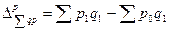; (8.63)

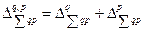. (8.64)

Агрегатный индекс общих затрат (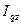) представляет собой произведение агрегатного индекса физического объема продукции (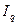) и агрегатного индекса себестоимости продукции (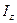) при условии, что коэффициенты соизмерения в индексе объема и веса в индексе себестоимости взяты из разных периодов:

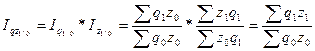; (8.65)

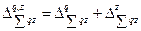; (8.66)

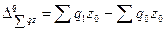; (8.67)

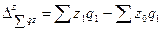. (8.68)