Для характеристики размера вариации признака используются абсолютные и относительные показатели. К абсолютным показателям вариации относятся: размах колебаний, среднее линейное отклонение. Среднее квадратическое отклонение, дисперсия, квартильное отклонение.
Размах колебаний (размах вариации):
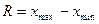, (5.11)
где хmax, xmin – соответственно максимальное и минимальное значения признака.
Величина показателя зависит от величины только двух крайних вариант и не учитывает степени колеблемости основной массы членов ряда.
Среднее линейное отклонение (
) и среднее квадратическое отклонение (
) показывают, на сколько в среднем отличаются индивидуальные значения признака от среднего его значения.
Среднее линейное отклонение определяется по формулам:
а) для несгруппированных данных (первичного ряда)
; (5.12)
б) для n вариационного ряда
. (5.13)
Среднее квадратическое отклонение () и дисперсия (
) определяются так:
а) для несгруппированных данных
; 
; (5.14)
б) для n вариационного ряда
; 
. (5.15)
Квартильное отклонение (dk) применяется вместо размаха вариации, чтобы избежать недостатков, связанных с использованием крайних значений:
, (5.16)
где Q3 и Q1 – соответственно третья и первая квартили распределения.
Квартиль – значения признака, которые делят ранжированный ряд на четыре равные по численности части. Таких величин будет три: первая квартиль (Q1), вторая квартиль (Q2), третья квартиль (Q3). Вторая квартиль является медианой. Вычисление квартилей аналогично вычислению медианы.
Сначала определяют положение или место квартили:
; 
; 
. (5.17)
Затем по накопленным частотам в дискретном ряду определяют численное значение.
В интервальном ряду распределения сначала указывают интервал, в котором лежит квартиль, затем определяют ее численное значение по формуле:
, (5.18)
где xQ – нижняя граница интервала, в котором находится квартиль;
S(Q-1) – накопленная частота интервала, предшествующего тому, в котором находится квартиль;
fQ - частота интервала, в котором находится квартиль.
При сравнении колеблемости различных признаков в одной и той же совокупности или же при сравнении колеблемости одного и того же признака в нескольких совокупностях с различной величиной средней арифметической используются относительные показатели вариации. Они вычисляются как отношение абсолютных показателей вариации к средней арифметической (или медиане) и чаще всего выражаются в процентах.
Формулы расчета относительных показателей вариации следующие:
коэффициент осцилляции 
; (5.19)
относительное линейное отклонение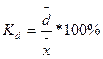 
; (5.20)
коэффициент вариации 
; (5.21)
относительный показатель квартильной вариации 
(5.22)
или 
. (5.23)
