Средние величины
Средней величиной называется обобщающий показатель, характеризующий типичный уровень варьирующего количественного признака на единицу совокупности в определенных условиях места и времени.
Объективность и типичность статистической средней обеспечивается лишь при определенных условиях. Первое условие – средняя должна вычисляться для качественно однородной совокупности. Для получения однородной совокупности необходима группировка данных, поэтому расчет средней должен сочетаться с методом группировок. Второе условие – для исчисления средних должны быть использованы массовые данные. В средней величине, исчисленной на основе данных о большом числе единиц (массовых данных), колебания в величине признака, вызванные случайными причинами, погашаются, и проявляется общее свойство (типичный размер признака) для всей совокупности.
Средняя величина всегда именованная, она имеет ту же размерность, что и признак у отдельных единиц совокупности.
В экономических исследованиях и плановых расчетах применяются две категории средних:
- степенные средние;
- структурные средние.
К категории степенных средних относятся: средняя арифметическая, средняя гармоническая, средняя квадратическая, средняя геометрическая. Величины, для которых исчисляется средняя, обозначаются буквой хi. Средняя обозначается через 
. Такой способ обозначения указывает на происхождение средней из конкретных величин. Черта вверху символизирует процесс осреднения индивидуальных значений. Частота – повторяемость индивидуальных значений признака – обозначается буквой f.
Формулы средних величин могут быть получены на основе степенной средней, для которой определяющей является управление:
, откуда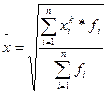 
. (5.1)
В дальнейшем при написании формул средних подстрочные значки i, n использоваться не будут, но подразумевается, что суммируются все произведения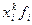 
.
В зависимости от степени k получаются различные виды средних величин, их формулы представлены в таблице 5.1.
Как видно из таблицы 5.1, взвешенные средние учитывают, что отдельные варианты значений признака имеют различную численность, поэтому каждый вариант «взвешивают» по своей частоте, т.е. умножают на нее. Частоты f при этом называются статистическими весами или просто весами средней. Однако необходимо учитывать, что статистический вес – понятие более широкое, чем частота. В качестве веса могут применяться какие-либо другие величины (в таблице 5.1 они обозначены буквой w). Например, при расчете средней продолжительности рабочего дня по предприятию единственно правильным будет взвешивание по количеству отработанных человеко-дней. Частоты отдельных вариантов могут быть выражены не только абсолютными величинами, но и относительными – частостями.
Вопрос о выборе средней решается в каждом отдельном случае, исходя из задачи исследования, материального содержания изучаемого явления и наличия исходной информации. Он состоит из нескольких этапов:
1) устанавливается определяющий показатель, т.е. обобщающий показатель совокупности, от которого зависит величина средней;
2) определяется математическое выражение для определяющего показателя;
3) производится замена индивидуальных значений средними величинами;
4) решение уравнения средней.
Основополагающее правило при этом заключается в том, что величины, представляющие собой числитель и знаменатель средней, должны иметь определенный логический смысл.
Таблица 5.1 - Формулы различных видов степенных средних величин
| Значение k | Наименование средней | Формула средней | |
| простая | взвешенная | ||
| -1 | Гармоническая |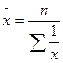 
|  ; 
|
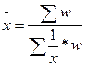
| Геометрическая |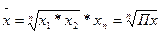  
| 
| |
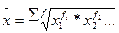
| Арифметическая |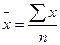 
|  ; 
| |
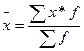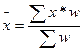
| Квадратическая |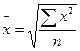 
| 
|
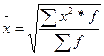
Структурные средние – мода и медиана – в отличие от степенных средних, которые в значительной степени являются абстрактной характеристикой совокупности, выступают как конкретные величины, совпадающие с вполне определенными вариантами совокупности.
Медианой называется значение признака, которое лежит в середине ранжированного ряда и делит этот ряд на две равные по численности части.
Ранжированный ряд – ряд, расположенный в порядке возрастания или убывания значений признака.
Для определения медианы сначала определяют ее место в ряду, используя формулу 5.2:
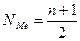, (5.2)
где n – число членов ряда.
Если ряд состоит из четного числа членов, то за медиану условно принимают среднюю арифметическую их двух срединных значений.
Модой называется значение признака, которое наиболее часто встречается в совокупности (в статистическом ряду).
Ряды распределения и приемы их построения
Различия индивидуальных значений признака у единиц совокупности называются вариацией признака. Она возникает в результате того, что индивидуальные значения складываются под совместным влиянием разнообразных условий (факторов), по разному сочетающихся в каждом отдельном случае.
Изучение вариации в пределах однородной группы предполагает использование следующих приемов: построение вариационного ряда (ряда распределения), его графическое изображение, исчисление основных характеристик распределения.
Вариационный ряд – групповая таблица, построенная по количественному признаку, в сказуемом которой показывается число единиц в каждой группе. Форма построения вариационного ряда зависит от характера изменения изучаемого признака, он может быть построен в форме дискретного или интервального ряда.
По характеру вариации значений признака различают:
- признаки с прерывным изменением (дискретные);
- признаки с непрерывным изменением (непрерывные).
Признаки с прерывным изменением могут принимать лишь конечное число определенных значений (например, тарифный разряд рабочих). Признаки с непрерывным изменением могут принимать в определенных границах любые значения (например, пробег автомобиля).
Для признака, имеющего прерывное изменение и принимающего небольшое количество значений, применяется построение дискретного ряда. В первой графе ряда указываются конкретные значения каждого индивидуального значения признака, во второй графе – численность единиц с определенным значением признака.
Для признака, имеющего непрерывное изменение, строится интервальный вариационный ряд, состоящий, так же как и дискретный ряд, из двух граф (варианты и частоты). При его построении в первой графе отдельные значения признака указываются в интервалах «от - до», во второй графе – число единиц, входящих в интервал. Интервалы образуются, как правило, равные и закрытые.
Вариационный ряд, состоящий из двух граф (варианты и частоты), иногда дополняются другими графами, необходимыми для вычисления отдельных статистических показателей или для более отчетливого выражения характера вариации изучаемого признака. Достаточно часто в ряд вводится графа, в которой подсчитываются накопленные частоты (S). Накопленные частоты показывают, сколько единиц совокупности имеют значения признака не больше, чем данное значение, и исчисляются путем последовательного прибавления к частоте первого интервала частот последующих интервалов.
Частоты ряда (f) могут быть заменены частостями (w), которые представляют собой частоты, выраженные в относительных числах (долях или процентах) и рассчитанные путем деления частоты каждого интервала на их общую сумму, т.е.
; 
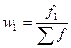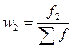и т.д. (5.3)
Если вариационный ряд дан с неравными интервалами, то для правильного представления о характере распределения необходимо произвести расчет абсолютной или относительной плотности распределения.
Абсолютная плотность распределения (p) представляет собой величину частоты, приходящейся на единицу размера интервала отдельной группы ряда: p = f / i. (5.4)
Относительная плотность распределения (p/) – частное от деления частости (w) отдельной группы на размер ее интервала: p/ = w / i. (5.5)
Следующим этапом изучения вариационного ряда является его графическое изображение.
Для наглядного представления вариационных рядов используют графические методы: полигоны распределения частот, гистограммы частот, кумулятивные кривые и т.п. Линейчатые и круговые диаграммы строятся для отображения структуры совокупности.
Полигон — ломаная кривая, строящаяся на основе прямоугольной системы координат, когда по оси X откладываются значения признака, а по оси Y — частоты.
Гладкая кривая, соединяющая точки, — эмпирическая плотность распределения.
Кумулята — ломаная кривая, строящаяся на основе прямоугольной системы координат, когда по оси X откладываются значения признака, а по оси Y — накопленные частоты.
Для дискретных рядов на оси откладываются сами значения признака, а для интервальных — середины интервалов.
Дискретный вариационный ряд изображается в виде полигона распределения частот. Для изображения интервального ряда применяются полигоны распределения частот и гистограмма частот. В ряде случаев для изображения вариационных рядов используются кумулятивная кривая (кумулята) и огива.
Для анализа вариационных рядов используются три группы показателей:
- показатели центра распределения;
- показатели степени вариации;
- показатели формы распределения.
