СОДЕРЖАНИЕ
Предисловие. 5
Введение. 7
Глава 1. Предмет и метод исследований математическими (статистическими) методами в лесном хозяйстве. 9
1.1. Примеры лесохозяйственных задач, решаемых с использованием математических методов. 9
1.2. Основные статистические определения, используемые при изучении курса «математические методы». 14
1.3. Метод исследования переменных (случайных) величин. 22
1.4. Вероятностный характер статистических выводов. 22
Глава 2. Измерение переменных величин и измерительные системы.. 27
2.1. Измерение физических величин. Понятие об измерениях. 27
2.2. Ошибки измерений. 28
2.3. Свойства случайных ошибок. 30
2.4. Измерительные системы.. 31
2.5. Международная система единиц (СИ), (SI). 32
2.6. Единицы, не входящие в СИ (SI) 33
2.7. Физические величины, часто применяемые в лесных измерениях. 34
2.8. Шкалы измерений. 35
Раздел 1. Анализ распределения. 37
Глава 1. Распределения случайных величин. 37
1.1. Что означает понятие «распределения» в статистических исследованиях? 37
1.2. Наблюдение. Формирование выборок. 40
Глава 2. Методы первичной обработки и анализа результатов измерений 45
2.1. Ранжирование данных наблюдения. 46
2.2. Группировка данных в вариационный ряд. 47
2.3. Графическое изображение вариационного ряда. 58
Глава 3. Статистические показатели распределения. 65
3.1. Статистики положения значений случайной величины.. 65
3.2. Статистики изменчивости значений случайной величины.. 74
3.3. Закон больших чисел. 79
3.4. Среднее квадратичное отклонение в нормальном распределении. 89
3.5. Статистики формы ряда распределения. 93
Предисловие
Учебное пособие предназначено для студентов специальностей 26-04, 26-05 и 32-08 высших учебных заведений.
В программе непрерывной математической подготовки инженеров лесного и садово-паркового хозяйства курс математических методов моделирования в лесном хозяйстве базируется на общем курсе высшей математики. Курс является общеобразовательным и направлен на формирование интеллектуального уровня студентов, развитие логического мышления, исследовательских начал.
В пособии учитывается специфика лесных объектов, являющихся предметом профессиональной деятельности инженеров лесного и садово-паркового хозяйства.
Задачи дисциплины состоят в обучении:
1. Приемам организации, планирования и осуществления наблюдения и эксперимента в лесном опытном деле и лесохозяйственном производстве;
2. Основным теоретическим и методическим направлениям применения математических методов моделирования в лесном хозяйстве.
3. Основам теории измерений и ошибок.
4. Навыкам верификации (проверки истинности, установления достоверности), интерпретации и практического применения математических моделей.
Студент, изучивший курс, должен уметь:
1. Планировать и проводить выборочные наблюдения и эксперименты для получения лесоводственной информации;
2. Проводить статистический анализ данных выборочных наблюдений и эксперимента, оценивать надежность полученных результатов;
3. Применять методы математического моделирования и готовые математические модели для решения задач лесного профиля;
4. Использовать полученные результаты для принятия решений в конкретных производственных и исследовательских ситуациях;
5. Применять пакеты статистических программ ЭВМ при проведении статистического анализа и математического моделирования.
Введение в МАТЕМАТИЧЕСКИЕ МЕТОДЫ МОДЕЛИРОВАНИЯ
Математические методы моделирования в лесном хозяйстве являются разделом математики и имели традиционное название математическая статистика. Предмет тесно связан с теорией вероятности, различие между которыми состоит в том, что они решают противоположные задачи. Теория вероятностей изучает закономерности распределения в генеральной совокупности для состава случайной выборки. Однако в практике приходится решать обратные задачи, когда известен состав выборки и по нему требуется определить, какой была или есть генеральная совокупность. Такого рода обратные для теории вероятности задачи и составляют предмет математических методов моделирования.
Математические методы моделирования занимают самостоятельное положение в табеле о науках.
Математические методы моделирования можно назвать теорией статистических решений, поскольку данный предмет характеризуется как наука об оптимальных решениях, основанных на статистических (выборочных) данных.
Статистическая теория количественного описания и анализа массовых явлений берет своё начало в XV1 – XV11 вв. Особенно стремительное развитие она получила в первой половине ХХ века. В Госсет (1876-1937) разрабатывает «теорию малой выборки», разработка английским ученым Р.А. Фишером (1890-1962) методов статистического анализа малых выборок (дисперсионный анализ) привела к широкому применению этих методов в практику принятия рациональных решений и в экспериментальные исследования.
Многолетняя история статистических методов показывает, что лучшие результаты дает их применение специалистами в конкретных областях практики. В лесном хозяйстве статистическая теория является инструментом для обоснования решений лесоводственных, таксационных, биологических и др. задач. Специалист лесного хозяйства должен хорошо владеть этим важнейшим инструментарием математические методы моделирования.
Математическая статистика в лесных вузах нашей страны насчитывает вековую историю. Большую роль в разработке статистических методов в лесоводстве сыграли труды профессоров-математиков М.Ю. Поморского, В.В. Голубева, А.Н.Дьячкова, А.К. Митропольского, читавших данный курс в лесотехнических вузах.
Большой вклад в популяризацию статистических методов, их внедрение в лесоводственные дисциплины внесли профессора-лесоводы К.Е. Никитин, А.З. Швиденко, М.Л. Дворецкий, Н.Л. Леонтьев, Н.Н. Свалов, О.А. Трулль, И.И. Гусев, Э.Н. Фалалеев, В.В. Кузьмичёв и др.
Студентов лесохозяйственных факультетов математическим методам моделирования обучают в большинстве случаев специалисты лесного хозяйства. В этом есть определенная закономерность, обусловленная тем, что статистические решения лесоводственных задач лишь дополняют решения лесовода, основанные на знании биологических законов и закономерностей. Существующие в природе закономерности в первую очередь становятся понятны лесоводу, а математические методы подтверждают и численно выражают выдвигаемые лесоводами гипотезы. Более успешное решение задачи подготовки специалистов лесного хозяйства в освоении курса математических методов моделирования возможно при участии в этом процессе математика-прикладника при ведущей роли высококвалифицированного специалиста лесного хозяйства. Совместный труд ученых математика и лесовода позволит достичь наилучших результатов.
Учебное пособие содержит сведения о теории и практике проведения исследований лесных объектов, методику сбора и обработки информации, объяснение точности и уровней вероятности статистических заключений.
Раздел 1. Общие вопросы подготовки к исследовательской работе
Глава 1. Объекты и метод исследований математическими методами в лесном хозяйстве
Прежде чем приступить к изучению математических методов исследования необходимо дать краткое описание задач, наиболее типичных для лесохозяйственной науки и практики. Это необходимо для ориентирования сознания читающего данный курс на объекты исследований и «привязки» приводимых ниже определений.
1.1. Примеры лесохозяйственных задач, решаемых
с использованием математических методов
Пример 1. В почвенном слое лесных питомников обитают личинки разных видов насекомых. В качестве пищи они используют корни сеянцев древесных и кустарниковых пород. В благоприятные для размножения годы численность личинок увеличивается настолько, что их деятельность приводит к повреждению сеянцев в больших количествах и становится целесообразным проведение мер борьбы с ними, которые зависят от вида и численности личинок. Следовательно, необходимо определить среднее количество личинок насекомых в почве на единице площади лесного питомника. Очевидно, что для этого следует взять почву слоем от поверхности до заданной глубины и подсчитать встречающиеся в этом слое личинки. Учитывая трудоемкость такой работы, неизбежно придем к выводу, что перекопать всю площадь и просеять всю почву на питомнике невозможно. Целесообразно сделать так, чтобы с минимумом затрат получить интересующие нас данные с достаточной точностью и надежностью. Обычно учет личинок ведут на площадках размером один квадратный метр. Площадки располагают так, чтобы учесть почвенное разнообразие питомника. В результате получают ряд чисел, например 8, 25,12, каждое из которых означает количество личинок на одном квадратном метре в разных местах площади питомника. Среднее количество личинок на одном квадратном метре равно сумме этих трех значений, деленной на 3. Отсюда среднее количество личинок на одном квадратном метре из приведенных трех равно 15.
Насколько близко число 15 подходит к действительной цифре заселенности почвы питомника личинками насекомых (к параметру)? Совершенно случайно может найденная средняя величина совпадать с действительной средней заселенностью личинок. С точностью 0 % (совсем без ошибки) можно установить среднюю заселенность почвы личинками только по результатам сплошной перекопки и просеивания всего почвенного слоя. В действительности, не проводя сплошного учета, можно дать приближенную, интервальную оценку искомой величины с определенной уверенностью в надежности вывода. Она получится, если найденное среднее значение уменьшить и увеличить на ошибку, происхождение и величину которой можно объяснить количеством просеянной почвы и величиной расхождения между собой данных в выборке. Ошибки в подсчете числа личинок, обусловленные невнимательностью или плохими условиями обеспечения эксперимента, не допускаются. Очевидно, что чем больше выборка, тем меньше ошибка и чем больше разность между числами в выборке (выше изменчивость), тем больше ошибка выборочного среднего значения. Задача, среди прочих, состоит в том, чтобы найти величину изменчивости признака и величину ошибки, выразить их мерой и числом.
Пример 2. Нередко специалистам лесного хозяйства приходится решать задачу по прогнозной оценке урожайности, например семян ореха кедра сибирского. Исходными данными для оценки урожайности может служить количество шишек на деревьях, произрастающих в определенных условиях. Трудоемкость подсчета очевидна. Невозможно подсчитать количество шишек на всех плодоносящих деревьях. Необходимы только выборочные наблюдения, но по определенным правилам, таким, чтобы любое дерево имело равную возможность попасть в выборку независимо от исполнителя этой работы. В противном случае результаты наблюдений могут оказаться ошибочными в том смысле, что они сильно будут зависеть от исполнителя. Если исполнитель будет выбирать деревья для учета по своему усмотрению, то результаты не могут обрабатываться статистическими методами. Закономерности массовых, случайных величин не распространяются на выборки, полученные необъективными способами.
Пример 3. Большое влияние на надежность выборочных средних величин оказывает степень однородности изучаемых генеральных совокупностей. Чем однороднее генеральная совокупность, тем ниже изменчивость изучаемого признака и меньше необходимый объем выборки для получения среднего значения с заданной точностью. Например, следует определить средний диаметр для стволов соснового древостоя, произрастающего на большой площади (десятки га). Предварительный осмотр древостоя показал, что часть деревьев находится на склоне, другая - на заболоченной низине, где условия произрастания совершенно другие.
Напрашивается решение о целесообразности определения среднего диаметра отдельно для деревьев на крутом склоне и для деревьев на заболоченной низине. Другими словами, необходимо весь сосновый древостой разделить, как минимум, на две генеральные совокупности. Одна расположена на крутом склоне, другая - на заболоченной низине. Кроме того, детальный осмотр сосняка на склоне показал, что в нем преобладающая часть деревьев имеет возраст около 80 лет, другая, меньшая по численности, но значительная по запасу стволовой древесины, имеет возраст около 200 лет. Очевидно, что определять один средний диаметр для обоих древостоев будет большой ошибкой. Он может оказаться таким, что деревьев в изучаемом древостое с диметрами, близкими к рассчитанному среднему диаметру, не окажется вовсе. Методически правильное решение состоит в том, что разновозрастный древостой следует разбить на два одновозрастных и определять средние диаметры для каждого древостоя в отдельности.
Пример 4. Есть примеры, когда границы и размеры генеральной совокупности не могут быть установлены. Например, следует рассчитать количество гумуса в почве. Для определения количества гумуса в почве необходимо взять какое-то количество почвы и в лабораторных условиях провести анализ. Будет получена цифра, характеризующая количество гумуса в данной пробе. Очевидно, что количество таких проб может быть взято как угодно большое. Все они будут составлять выборку из генеральной совокупности. Размер всей генеральной совокупности неизвестен и не может быть определен. Генеральной совокупностью здесь является слой почвы в определенных лесорастительных условиях. Для его характеристики должна быть взята выборка достаточного объема.
Пример 5. Есть генеральные совокупности, которые как бы не существуют вовсе и, тем не менее, для их характеристики составляют выборки, которые обрабатывают математическими методами с целью определить выборочное среднее значение и его вероятную ошибку. В качестве примера можно привести эксперимент по оценке нового способа обработки почвы. Эффективность нового способа обработки почвы можно оценить специально поставленным экспериментом. Он может заключаться в том, что на небольшой площади будет проведена обработка почвы традиционным способом в некотором количестве повторений и рядом с ними заложены опытные площадки, обработанные по новой технологии. Эффективность обоих методов обработки почвы можно оценивать по приживаемости, по приросту, по урожайности и т.д. Так может быть получена выборка, а что здесь является генеральной совокупностью? Она не существует и размер генеральной совокупности установить невозможно, поскольку сам эксперимент проводится только с необходимым для заданной точности количеством повторений.
Пример 6. Оценка всхожести семян связана с проращиванием их в лабораторных условиях. Эксперимент по оценке всхожести также должен предусматривать определение средней величины всхожести и статистическое обоснование надежности полученного результата. Теория статистических исследований переменных величин требует организовать получение выборки так, чтобы она надежно характеризовала всю партию семян. В эксперименте должна быть получена всхожесть в нескольких повторностях, это позволит установить изменчивость всхожести и рассчитать среднее значение с ошибкой выборки.
Пример 7. Есть другой класс задач, решаемых также с применением статистических методов. Например, требуется определить возраст деревьев в древостое. Наиболее надежным способом определения возраста деревьев является подсчет числа годичных слоев на пне спиленного дерева. Это и трудоемкое дело и связано с уничтожением предмета изучения. Однако, возраст можно установить по косвенным признакам, таким, как толщина коры, наличие и глубина трещин в коре, цвет коры, диаметр дерева, форма кроны и др. Способ решения задачи состоит в том, чтобы установить зависимость возраста от многих перечисленных показателей. Если такая зависимость будет установлена, то её можно использовать для определения возраста через толщину коры, глубину трещин в коре и так далее. Надежность вывода о возрасте дерева будет зависеть от объема выборки и степени зависимости возраста от косвенных признаков. Математическими методами по выборке из данных толщины коры, её цвету и т.д. можно делать вероятностные заключения о возрасте дерева, говоря вообще, по выборке оценивать генеральную совокупность. Зависимость возраста от внешних признаков можно выразить математическими и графическими моделями.
1.2. Основные определения, используемые
в математических методах моделирования
После того, как вы получили некоторое представление о лесохозяйственных задачах, решение которых требует применения математических методов, можно перейти к формулированию часто используемых статистических определений. Прежде всего, необходимо дать определение тому, что является предметом (объектом) исследований математическими методами.
Предметом исследований математическими методами являются случайные величины
Под категорию «случайных величин» вполне подпадают приведенные выше объекты лесохозяйственной деятельности. Это и диаметры деревьев, и численность личинок на единице площади лесного питомника, и всхожесть семян и так далее. Все они обладают общим свойством принимать различные значения без очевидных на то оснований для их разнообразия. Изменяется количество личинок на 1 м2 питомника, имеют различные значения диаметры стволов в одновозрастном древостое, варьирует всхожесть семян в пробах из одной партии и тому подобное. Везде изучаемое свойство, качество признака, величина отдельных единиц из множества находятся под воздействием большого числа разнообразных и сложным образом взаимодействующих факторов, число которых учесть полностью и оценить влияние каждого из них отдельно невозможно. В результате совместного, разнонаправленного действия таких факторов отдельные значения изучаемой величины оказываются неодинаковыми, переменная величина является изменчивой, а сама изменчивость носит случайный характер. Однако случайный характер изменчивости признака не означает отсутствие какой-либо закономерности
Случайной величиной называют такую величину, которая под влиянием многих разнонаправленных, одновременно действующих факторов принимает различные значения в каких-то пределах.
Для обнаружения каких-либо закономерностей изучаемой случайной величины необходимо произвести достаточно большое число наблюдений. Например, для того, чтобы проявилась закономерность в распределении стволов по диаметру, необходимо обмерить, по крайней мере, 100 и более деревьев. Отсюда возникло еще одно понятие - массовое явление.
массовое явление – это необходимое свойство изучаемой случайной величины, которое обеспечивает наблюдение или эксперимент в практически одинаковых условиях
Получить представление о характере распределения деревьев по диаметру можно путем осмотра древостоя, отмечая каких деревьев больше, каких меньше. Если древостой одновозрастный, то большинство деревьев имеют диаметры, близкие к среднему арифметическому диаметру. По мере отдаления диаметров деревьев от среднего диаметра, как в большую, так и в меньшую сторону, количество деревьев снижается. Подтвердить это экспериментально можно только путем обмера достаточно большого количества деревьев. Например, обмер диаметров деревьев по 4-х сантиметровым ступеням толщины покажет, что в начале эксперимента никакой закономерности в распределении не проявляется. Продолжая обмер деревьев до нескольких десятков деревьев можно увидеть, что количество стволов в центре ряда увеличивается быстрее, чем по краям ряда. На рис. 1а показано распределение по диаметру 10 стволов (начало перечета). На рис 1б показано распределение 100 стволов того же древостоя.


Рис 1а Рис 1б
На левом графике (рис 1а) показано распределение 10 стволов, где никакой закономерности в распределении стволов не проявляется. На правом графике (рис 1б) показано распределение 100 стволов. По нему можно видеть, что наибольшее количество стволов имеют диаметры 22-30 см.
По мере продолжения обмера стволов, форма расположения точек на графике изменяется все медленнее, а график все точнее отражает распределение стволов, имеющееся в генеральной совокупности. Имеет место быть устойчивость явления.
Статистическая устойчивость – это стабильность распределения значений в выборке, достижение которой позволяет по выборке оценивать характеристики случайной величины в генеральной совокупности.
Чтобы узнать, как распределятся учетные площадки по количеству личинок на одном квадратном метре недостаточно иметь 5-10 площадок. Количество площадок нужно увеличивать до тех пор, пока характер распределения не станет устойчивым. Только с достижением устойчивости в распределении можно говорить о том, что выборочная совокупность надежно характеризует переменную величину генеральной совокупности. Пока не достигнуто состояние устойчивости распределения единиц в выборке, характеристика генеральной совокупности по выборке не надежна.
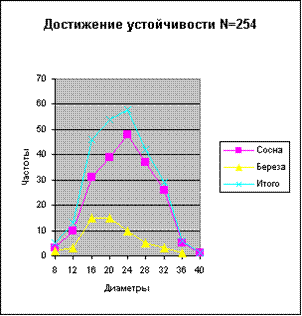
Чтобы закрепить представление о статистической устойчивости распределения проведите следующий эксперимент. Подберите однородный по составу и возрастной структуре древостой на достаточно большой площади, в составе которого 80 % деревьев сосны и 20 % деревьев березы. Древостой можно заменить имитационной моделью, планом, на котором условными знаками показать размещение деревьев сосны и березы. Проведите перечет деревьев по ступеням толщины в пять этапов. На первом этапе методом случайного отбора возьмите в перечет 10 деревьев сосны и березы вместе, на втором этапе количество деревьев в перечете доведите до 50 деревьев, третьем – до 100 деревьев, четвертом – до 200 деревьев и в пятом этапе – до 254 деревьев. Результаты перечета приведены в таблице 1. Графические изображения поэтапного перечета показаны на рис 2 – 4. Итоги 1-4 этапов перечета не позволяют утверждать, что характер кривой распределения в генеральной совокупности несущественно отличается от распределения стволов в выборке. Итоги перечета на 5 этапе несущественно изменили форму линии на графике по сравнению с 4 этапом. Можно говорить о достижении состояния устойчивости. Таким образом, для достижения состояния устойчивости выборочная совокупность должна быть достаточно большого объема.
| Таблица 1 | Этапы перечета деревьев по диаметру | ||||||||
| 1 этап | 2 этап | ||||||||
| Ступени толщины, см | Порода | Ступени толщины, см | Порода | ||||||
| Сосна | Береза | Итого | Сосна | Береза | Итого | ||||
| число стволов | Число стволов | ||||||||
| Итого, шт. % | Итого, шт % | ||||||||
| 3 этап | 4 этап | ||||||||
| Ступени толщины, см | Порода | Ступени толщины см | Порода | ||||||
| Сосна | Береза | Итого | Сосна | Береза | Итого | ||||
| Число стволов | Число стволов | ||||||||
| Итого, шт | Итого, шт | ||||||||
| % | % | 81,5 | 18,5 | ||||||
| Окончание табл.1 | 5 этап | ||||||
| Ступени толщины см | Порода |
| |||||
| Сосна | Береза | Итого | |||||
| Частота – число стволов | |||||||
| Итого, шт | Рис 2. Линии распределения | ||||||
| % | в состоянии устойчивости | ||||||
| |||||||
| Рис 3. Этапы достижения | Рис 4. Этапы достижения | ||||||
| устойчивости | устойчивости | ||||||
Совокупность всех возможных значений случайной величины, находящихся в одинаковых условиях, называется генеральной совокупностью.
Выборочная или частичная
совокупность- это некоторое число значений, взятых из генеральной совокупности.
Объем выборки, это количество всех единиц значений, составляющих одну выборку.
Другими словами, сколько деревьев попало в перечет, это и есть объем выборки.
В теории вероятностей используется такое понятие как случайное событие. В примере с поэтапным перечетом деревьев в качестве случайного события можно рассматривать любую ступень толщины стволов. В ходе перечета заранее неизвестно, какой диаметр у следующего обмеряемого дерева. Распределение деревьев разной толщины по площади древостоя имеет случайный характер.
Случайное событие-
это такое событие, которое в результате эксперимента или наблюдения может произойти, а может и не произойти.
Случайная величина и случайное событие. Что в них общего и в чем различие?
Чтобы избежать путаницы в определениях следует подчеркнуть имеющиеся различия в определении случайной величины и случайного события. Случайными событиями можно назвать диаметры ствола определенной величины. Например, ступени толщины 8 см, 12 см и т.д. можно отнести к категории случайных событий. Случайная величина может содержать в себе несколько случайных событий. Например, объект изучения диаметр деревьев есть случайная величина. Случайным событием можно назвать группу значений случайной величины, представляющую некоторый интерес для исследователя.
Частота случайного события есть число повторений одинаковых значений случайной величины.
В таблице 1 количество стволов по ступеням толщины называются частотами.
Частость случайного события – это частное от деления частоты на объем выборки.
Таблица 2– Определение устойчивой частости событий при перечете
Порода - сосна
| Ступени | Этапы перечета | |||||||||
| Частота | Частость | Частота | Частость | Частота | Частость | Частота | Частость | Частота | Частость | |
| 0,17 | 0,04 | 0,03 | 0,02 | 0,015 | ||||||
| 0,17 | 0,08 | 0,07 | 0,06 | 0,050 | ||||||
| 0,33 | 0,16 | 0,11 | 0,11 | 0,155 | ||||||
| 0,08 | 0,21 | 0,20 | 0,195 | |||||||
| 0,24 | 0,22 | 0,26 | 0,24 | |||||||
| 0,33 | 0,08 | 0,15 | 0,16 | 0,185 | ||||||
| 0,20 | 0,12 | 0,15 | 0,13 | |||||||
| 0,12 | 0,07 | 0,03 | 0,025 | |||||||
| 0,02 | 0,01 | 0,005 | ||||||||
| Σ |

Рис 5. Достижение устойчивой частости распределения
по диаметру стволов сосны
Вывод, который следует сделать из этого эксперимента в пяти этапах, состоит в том, что по мере увеличения объема выборки частости приближаются к вероятностям. Вероятностями для данного эксперимента являются частости, вычисленные по данным перечета всей генеральной совокупности. Перечет для генеральной совокупности можно получить в результате обмера всех деревьев породы в выделе.
1.3. Вероятностный характер статистических выводов
Достижение устойчивости в величине частости события дает возможность по частостям событий делать достаточно надежные выводы о вероятностях этих событий.
Вероятность события получится, если число случаев, благоприятствующих данному событию, разделить на общее число случаев.
Например, в древостое имеются деревья разных диаметров: - 20% деревьев имеют диаметры 12см, 30% имеют диаметры 16см, 40% - 20см и 10% имеют диаметры 24см. Всех деревьев разных диаметров 100%. Спрашивается, чему равна вероятность такого события, что первое встреченное в этом древостое дерево будет иметь диаметр 20см? Вероятность такого события можно вычислить путем деления числа деревьев с таким диаметром на общее количество деревьев в древостое. Вероятность того, что первое встреченное в таком лесу дерево будет иметь диаметр 20 см, равна 0,20 или 20 %.
Если вероятность обозначить буквой «p », число случаев проявления события буквой «m », общее число случаев буквой «n », то формулу вероятности можно записать так:
p = m/n. (1)
Следовательно, вероятность может принимать значения от 0 до 1 всегда со знаком плюс. Вероятность, равная 1, означает, что все 100% случаев благоприятны только одному событию. Это может быть в древостое, где все деревья имеют одинаковый диаметр, или когда во всех почвенных ямах равное количество личинок, или если всхожесть семян одинаковая во всех пробах и т.д. Вероятность события, равная 1.0, указывает на полное отсутствие альтернативы.
В теории вероятностей в тесной связи с вероятностями событий находится так называемый ЗАКОН БОЛЬШИХ ЧИСЕЛ.
Закон больших чисел имеет место при любой постоянной вероятности события при отдельном испытании. Простейший вид закона больших чисел называется теоремой Бернулли.
Теорема Бернулли. Если имеется неограниченный ряд независимых испытаний, при каждом из которых вероятность некоторого события остается постоянной, то при достаточно большом числе испытаний будет сколь угодно близкой к достоверности вероятность того, что отношение числа появлений события к числу испытаний произвольно мало отличается от вероятности события при отдельном испытании.
Закон больших чисел исключительно важен при научных исследованиях. На основании этого закона можно с необходимой уверенностью ожидать приближенное равенство между установленными из наблюдений частостями некоторых событий и их вероятностями, а также мы можем по вероятности события судить о том, как часто событие будет повторяться.
Основное положение закона больших чисел вскрывает сущность математических методов анализа и моделирования. При испытаниях в одной повторности достоверность результата неизвестна. Но при достаточно большом числе испытаний (повторностей) частости появлений того или иного события приближенно равны их вероятностям. Другими словами, закон больших чисел показывает, что заключения, неприменимые к каждому отдельному значению, оказываются вполне обоснованными по отношению к достаточно большой совокупности однородных значений. Теорема Бернулли нашла свое подтверждение в приведенном выше эксперименте поэтапного перечета деревьев.
К приведенному выше примеру вычисления среднего количества личинок на квадратном метре питомника теорема Бернулли имеет прямое отношение. На первой площадке 8 личинок, на второй - 25 личинок, на третьей - 12 личинок. Полученное среднее арифметическое значение 15 личинок на одном квадратном метре питомника не является величиной достаточно достоверной. Из трех испытаний все дали далекий результат по числу личинок от вычисленного среднего значения. Следовательно, вероятность того, что среднее значение в генеральной совокупности (для всего питомника) будет близка к цифре 15, очень низка.
Несколько забегая вперед, отметим, что с вероятностью 0,95 среднее значение равно 15 личинкам плюс-минус 3 личинки. Нужно, чтобы в этот интервал входило не менее 95 % благоприятных случаев. Нижняя граница интервала 12 личинок, верхняя граница интервала 18 личинок. Из трех значений (8, 25, 12) в этот интервал входит только одна площадка из трех. Следовательно, вероятность того, что среднее количество личинок на квадратном метре питомника находится в заданном интервале, равна:
p=1/3 или 0,33.,
что недостаточно.
Для повышения вероятности заключения необходимо увеличивать количество площадок, так как уменьшить степень изменчивости данной переменной величины невозможно по условию задачи. Изменчивость числа личинок на питомнике в данное время - это характеристика, аналогичная засоренности, изменить которую можно только проведением каких-то мероприятий, например прополки сорняков.
Теоремы сложения вероятностей
Здесь применено следствие из теоремы 1 сложения вероятностей совместных событий. Согласно теореме 1 вероятность появления двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
P(A+B) = P(A) + P(B) - P(AB). (2)
Следствие теоремы 1 гласит: «вероятность появления суммы двух несовместных событий равна сумме вероятностей этих событий».
P(A+B) = P(A) + P(B). (3)
В эксперименте с монетой и с диаметрами деревьев следует рассматривать и различные плоскости монеты, и разные диаметры деревьев как несовместные события. За одно бросание монеты не может быть события, когда монета упадет сразу обеими плоскостями. Аналогично можно рассуждать и в опыте по обмеру диаметров деревьев. Лесовод не может измерять одновременно два и более диаметров, значит два диаметра - два несовместных события.
Не возникает противоречия и в случае применения следствия к вычислению вероятности суммы более двух несовместных событий.
P(A+...+N) = P(A) +...+ P(N). (4)
На примере древостоя, в котором 20 % деревьев имеют диаметры 12 см, 30% имеют диаметры 16 см, 40% - 20см и 10% имеют диаметры 24см, покажем, чему равна вероятность того, что диаметр взятого наугад дерева попадет в интервал от 16 до 20 см включительно? Всех деревьев разных диаметров в древостое 100%. Число случаев, благоприятствующих встрече дерева с диаметрами от 16 до 20 см, составляет 70 (30% + 40%) из ста. Следовательно, вероятность того, что первое дерево в начале обмера по толщине попадет в интервал от 16 до 20 см, составит 0,70. Эта вероятность могла быть получена как сумма вероятностей для стволов 16 см (0,30) и для стволов 20см (0,40).
Теорема 2. Вероятность появления события « В», противоположного событию « А», равна разности между 1 и вероятностью наступления события А:
P(B) = 1 - P(A). (5)
Следствие теоремы 1сложения вероятностей лежит в основе вывода функции распределения случайной величины:
F(x) = å P(X = xi)., (6)
при условии, что xi < x.
(О.А. Шушерина. Высшая математика. Теория вероятностей.)
Теорема 2 используется в обосновании элементарных статистических выводов. Подробнее об этом будет изложено в главе 4 «оценка параметров».
1.4. Метод исследования переменных (случайных)
величин
Метод оценки генеральной совокупности по данным выборочных наблюдений называется
статистическим методом
Статистический метод используется всеми лесными науками и практикой лесного хозяйства. Обусловлено это тем, что переменные величины варьируют и надежность выводов об их свойствах зависит от степени изменчивости значений и объема выборки. На ошибки заключений по выборочным наблюдениям могут оказывать влияние и ошибки измерений, обусловленные использованием неисправных инструментов, проведением измерений в неблагоприятных условиях.
Поэтому важно иметь и правильно применять соответствующие инструменты и измерительные системы. Измерительные приборы и инструменты подлежат систематическим поверкам.
Также важно обеспечивать единообразие в использовании символов для обозначения тех или иных физических величин, что облегчит передачу информации математическими моделями. К сожалению, в настоящее время в научной литературе и производственных инструкциях для обозначения одних и тех же переменных величин нередко используются различные символы. Это затрудняет взаимопонимание, поэтому важно знать и строго соблюдать приведенные ниже измерительные системы.
Глава 2. Измерение переменных величин и измерительные системы
Из рассмотренных примеров ясно, что изучение природных объектов предполагает, в том числе, измерение длин, площадей, объемов, температуры и др. с последующей статистической обработкой результатов измерений. Необходимо знать и строго соблюдать в своей работе правила измерения физических величин во избежание трудно выявляемых ошибок.
2.1. Измерение физических величин. Понятие об измерениях
«Измерить» означает определить какой-нибудь мерой величину чего-нибудь. Измерить температуру, измерить длину ствола, измерить диаметр круга. Мерой называют единицу измерения, единицу учета. Мера длины, мера объема, мера площади и т.д. Измерение представляет собой сравнение измеряемой величины с другой величиной, принятой за единицу сравнения. Например, измерить длину ствола означает определить количество единиц измерения, которые могут быть расположены по его длине последовательно одна единица за другой. Единицей измерения длины стволов является один метр (1м). Каждое измерение протекает при наличии и взаимодействии следующих пяти факторов:
1. Объекта измерения;
2. Субъекта измерения, т.е. лица или автоматического устройства, осуществляющего процесс измерения;
3. Мерного прибора, посредством которого субъект или автоматическое устройство производит измерение объекта;
4. Способа измерения, т.е. совокупности тех действий, которые составляют процесс измерения;
5. Внешней среды, в которой протекает измерение.
Совокупность всех перечисленных факторов составляют условия измерения.
Результат измерения (например, объем бревна V=0.5м3) можно записать в форме уравнения:
V = n_u, (7)
где V - измеряемая величина;
n - количество единиц измерения, соответствующее измеряемой величине;
u - наименование единицы измерения.
Измерения могут быть прямыми и косвенными. Примером прямого измерения является измерение длины срубленного дерева рулеткой или мерной лентой. Пример косвенного измерения - измерение высоты растущего дерева высотомером. Здесь прямым способом измеряются: а) расстояние от точки измерения на местности до дерева, б) углы наклона линий от глаз субъекта до вершины дерева (одна линия) и до основания дерева (другая линия) к горизонтальной линии. Высота частей ствола вычисляется по известным геометрическим формулам. Высота ствола получается как сумма высот частей ствола ниже горизонтальной линии и выше горизонтальной линии.
2.2. Ошибки измерений
Условия измерения предопределяют возможные ошибки измерений. Ошибкой считается величина отклонения результата измерения от истинного значения измеряемого объекта. Очевидно, что ошибки измерений бывают как со знаком плюс, так и со знаком минус. Если результат измерения оказался меньше истинного значения, это означает, что допущена ошибка измерения со знаком минус, если больше - со знаком плюс. Сказанное можно выразить следующим уравнением:
@ = q - Q, (8)
где @ - ошибка измерения,
q - результат измерения (что есть),
Q - истинное значение (что должно быть).
Иначе можно сказать: ошибка равна тому, что есть, минус то, что должно быть. Ошибка имеет знак минус, если результат измерения меньше истинного значения и знак плюс, если результат измерения больше истинного значения.
Каждый из пяти факторов измерений может порождать ряд элементарных ошибок, совокупность которых дает общую ошибку. Все элементарные ошибки измерения можно подразделить на 2 класса: систематические и случайные. Суммарное влияние систематических элементарных ошибок порождает систематическую часть общей ошибки результата измерений, а все вместе случайные элементарные ошибки порождают случайную часть общей ошибки:
@ = У + ", (9)
где: @ общая ошибка;
У систематическая часть;
" случайная часть.
Систематическая ошибка
Систематические элементарные ошибки порождаются главными, существенными связями между факторами измерений и возникают всякий раз при данных условиях измерений. Систематические ошибки могут происходить чаще всего по вине субъекта измерения. Это, главным образом, работа ошибочно настроенным инструментом. Поэтому перед процессом измерений полагается проводить поверку измерительным инструментам специальными приемами с последующей регулировкой и снижением систематической ошибки измерения до нуля. Если систематическая ошибка обнаружена после проведения измерений, то ее можно легко исправить путем введения ее с обратным знаком в результаты измерений.
Граница между систематической и случайной ошибками не всегда четкая.
Случайные ошибки
Случайные элементарные ошибки порождаются второстепенными связями между факторами измерений, они могут быть, а могут и не появиться при данных условиях измерений. Исключить совершенно случайные ошибки невозможно, учесть их можно только в среднем.
Грубые ошибки
Кроме перечисленных двух классов ошибок иногда в результаты измерений попадают грубые ошибки (промахи). Они резко отклоняют результаты измерений от действительных значений измеряемых величин, поэтому должны обязательно своевременно исключаться. Одним из действенных способов недопущения грубых ошибок является сравнение инструментального результата с глазомерной оценкой в момент измерения. Например, грубая ошибка считывания диаметра ствола с линейки мерной вилки может быть обнаружена, если исполнитель при этом оценит диаметр «на глаз».
2.3. Свойства случайных ошибок
Случайные ошибки измерений являются ярким примером случайной величины, пригодной для исследования статистическими методами. Они обладают следующими основными свойствами:
1. Свойство ограниченности состоит в том, что при данных условиях измерений абсолютное значение случайной ошибки не может превзойти некоторого предела. Этот предел называется случайной предельной ошибкой измерения. В качестве предела случайной ошибки при измерении диаметра ствола мерной вилкой можно считать цену деления на линейке, равную 0.5 см.
2. Свойство компенсации - среднее арифметическое значение случайных ошибок при неограниченном увеличении количества повторных измерений стремится к нулю.
3. Свойство симметричности - при достаточно большом числе измерений одинаковые по абсолютной величине, но разные по знаку случайные ошибки встречаются с одинаковой частотой;
4. Свойство распределения по величине - при достаточно большом числе измерений наибольшие по абсолютной величине случайные ошибки встречаются реже, чем малые. Чем больше случайная ошибка, тем реже она встречается.
2.4. Измерительные системы
Для осуществления измерения необходимо располагать не только нужными измерительными приборами, но и установить единые для всех исполнителей соответствующие целям единицы измерения, которые объединяются в некоторую систему. До 1963 года были приняты три метрические системы единиц:
1. Абсолютная физическая система СГС (CGS), в которой основными единицами являются сантиметр, грамм, секунда;
2. Абсолютная практическая система МКС (MKS), в которой основными единицами являлись метр, килограмм и секунда;
3. Техническая система МКГСС (MKGS), в которой основными единицами являлись метр, килограмм-сила и секунда.
2.5. Международная система единиц (СИ), (SI).
В настоящее время повсеместно применяется принятая в 1960 году единая Международная система единиц. На всех языках мира эта система получила сокращенное название СИ (SI), а ее единицы называются единицами СИ.
Основные единицы СИ
В международной системе единиц измерения (СИ) в качестве основных используются следующие 7 единиц:
· единица длины метр (м),
· единица времени секунда (с),
· единица массы килограмм (кг),
· единица силы электрического тока ампер (А),
· единица температуры кельвин (К),
· единица количества вещества моль (моль),
· единица силы света кандела (кд).
Производные единицы СИ
Все остальные единицы Международной системы представляют собой произведения степеней основных единиц, не содержащие численных коэффициентов, или, иначе говоря, образуются когерентно (имеют постоянное соотношение) из основных единиц. Другие единицы являются некогерентными и потому не входят в СИ.
Десятичные кратные и дольные единицы
Единицы Международной системы при практическом использовании часто оказываются слишком большими или слишком малыми. Поэтому с помощью особых приставок могут быть образованы десятичные кратные и дольные единицы, если это не запрещено в отдельных случаях. Существуют некоторые правила использования приставок, приведем важнейшие из них:
· Единица измерения не может содержать более одной приставки.
· Комбинация сокращенного обозначения приставки и единицы измерения составляет единый символ, который можно возводить в степень; при этом скобки не применяются. Иными словами, если единица возводится в какую-либо степень (желательно целочисленную), то в ту же степень возводится и десятичная приставка.
· Приставки единиц измерения следует выбирать таким образом, чтобы численное значение результата лежало в области 0,1...1000.
Таблица 2 –Приставки к единицам СИ
| Приставка | Краткое обозначение | Значение | Приставка | Краткое обозначение | Значение |
| дека | да | деци | д | 10-1 | |
| гекто | г | 102 | санти | с | 10-2 |
| кило | к | 103 | милли | м | 10-3 |
| мега | М | 106 | микро | мк | 10-6 |
| гига | Г | 109 | нано | н | 10-9 |
| тера | Т | 1012 | пико | п | 10-12 |
| пета | П | 1015 | фемто | ф | 10-15 |
| экса | Э | 1018 | Атто | а | 10-18 |
2.6. Единицы, не входящие в СИ (SI)
Эти единицы выводятся не когерентно. Из-за важной роли, какую играют такие единицы в науке, технике и экономике, их разрешается применять в определенных областях в течение ограниченного, а в ряде случаев и неограниченного времени. Некоторые из них используются в специальных областях.
Единицы с десятичной кратной или дольной приставкой называются некогерентными и не входят в СИ. Однако они также являются законными единицами, например 1 километр (1км) =103 м.
2.7. Физические величины, часто применяемые
в лесных измерениях
В целях лучшего взаимопонимания и повышения однозначности трактовки тех или иных результатов измерений, необходимо придерживаться единой системы обозначений результатов измерений. Например, укоренившееся обозначение площади буквой S не соответствует признанному обозначению в международной системе единиц. Возраст у нас принято обозначать буквой «А», но как следует из приведенной ниже таблицы, буквой А обозначают площадь.
Таблица 3 – Единицы измерения случайных величин
| Физическая величина | Обозначения | Единица измерения, краткое обозначение, соотношение между единицами | Примечание |
| Длина | l, s, r | метр, м световой год, св. год = 9,4605*1015 | ОЕ (н) |
| Площадь | A | м2 гектар, га=104 м2 | СИ (н) |
| Объем | V | м3 литр, л=10-3м3=1 дм3 | СИ н |
| Плоский угол | a, j | радиан, рад = м/м=1 градус, 1o=1,745329*10-2 рад минута, 1ў =1o/60=2,908882*10-4 секунда, 1І =1ў/60=1o/3600=0,484814*10-5 рад | СИ н н н |
| Время | t | секунда, с минута, мин = 60 с час, ч = 60 мин = 3600 с сутки, сут=24 ч = 1440 мин = 86400 с | ОЕ н н н |
| Скорость | n | м/с км/ч = 1/3,6 м/с=0,277778 м/с | СИ н |
| Масса | m | килограмм, кг грамм, г=10-3кг тонна, т=103 карат, кар=0,2 г=2*10-4кг | ОЕ н н (огр) |
| Плотность | p | кг/м3 кг/дм3=т/м3=103кг/м3 г/см3 | СИ КД КД |
| Температура Кельвина | T | кельвин, К | ОЕ |
| Температура Цельсия | t | градус Цельсия, oС t=T-T0=273.15 К | н |
Примечание: ОЕ основная единица,
СИ единица СИ,
н единица с неограниченной областью и неограниченным сроком применения,
(н) единица с неограниченным сроком, но специальной областью применения,
КД десятичная кратная и дольная единица СИ
2.8. Шкалы измерений
Слово «шкала» в переводе с латинского языка означает:
1. Линейка или циферблат с равными интервалами в различных измерительных приборах;
2. Ряд цифр, или величин, расположенных в нисходящем или восходящем порядке через равные интервалы.
Лесоводы могут изучать разнообразные объекты: - диаметры стволов, формы крон, - овальные, конусовидные и др.; окраску семян или пыльников, - красные, желтые, белые; степень развития, - лучшие, отставшие в развитии. Измеряя и оценивая объекты, лесоводы получают «данные». Термин «данные» весьма популярен в научных исследованиях. Очевидно, что измерить диаметр можно различными приборами, имеющими линейку или циферблат. Результаты обмера (данные) - численная величина. Однако измерять форму кроны, или цвет листьев и тому подобное приборами пока не могут и ограничиваются глазомерной оценкой качественного признака. Поэтому шкалы измерений подразделяют на качественные и количественные.
Качественные шкалы - шкала наименований и порядковая шкала.
Шкала наименований используется для классификации индивидуумов в генеральной или выборочной совокупности. Например, все разнообразие цветовых оттенков семян кедра можно разбить на классы: а) темные, б) светлые. Могут быть и другие варианты оттенков. Структура шкалы наименований не изменится, если классы поменять местами, или вместо буквенных обозначений применить цифровые обозначения.
Порядковая шкала позволяет не только разбивать индивидуумы на классы, но и упорядочить сами классы. Каждому классу присваивается различное обозначение (буквенное или цифровое), но так, чтобы порядок обозначений соответствовал упорядоченному изменению уровня индивидуума от меньшего к большему или от большего к меньшему уровню. Если нумеровать классы, то они должны находиться в цифровом порядке, если обозначать классы буквами, то классы должны располагаться в алфавитном порядке. Например, те же семена кедра можно разгруппировать на три класса по цветовому оттенку: а) темные, б) средние и в) светлые. В данном случае применена порядковая шкала, так как упорядочены сами классы в порядке убывания густоты цвета. Характеристика изменчивости цветового оттенка семян не претерпит изменения, если классы расположить в обратном порядке – от светлого к темному оттенку.
Количественные шкалы - шкала отношений и интервальная шкала.
Шкала отношений. Эта шкала позволяет классифицировать и упорядочивать индивидуумы, а также количественно оценивать различие между классами. Она имеет единицу измерения, и в ней задано абсолютное начало отсчета. Например, диаметр величиной 20 см принадлежит шкале отношений, в которой 0 см есть фиксированное начало отсчета, а 1см - единица измерения. В этой шкале можно определить, во сколько раз одно измерение превосходит другое, например, диаметр 24 см в два раза больше диаметра 12 см.
Интервальная шкала. Она имеет единицу измерения и произвольное начало отсчета. Структура интервальной шкалы не изменяется при линейном преобразовании вида x` = ax + b, a>0. Это преобразование смещает начало на b единиц и изменяет единицу измерения в a раз. Преобразование x` = 0.55x-17.8, где x - температура по Фаренгейту, переводит шкалу Фаренгейта в шкалу Цельсия.
Нормальная температура человека по Цельсию равна 36.6 градуса. По уравнению вычислим нормальную температуру человека по Фаренгейту:
x = (x` + 17,8)/0,55 = (36,6 + 17,8)/0,55 = 98,9.
Раздел 2. Анализ распределения
Глава 1. Распределения случайных величин
1.1. Что означает понятие «распределения»
в статистических исследованиях?
Таблица 4. – Распределение.
| Значения случайной величины | Частоты | ||||||||||
Дата добавления: 2016-12-06; Мы поможем в написании ваших работ!; просмотров: 1825 | Нарушение авторских прав Поиск на сайте: Лучшие изречения: |
Ген: 0.016 с.