Пусть в пространстве даны две точки М1 и М2. Говорят, что точка М делит отрезок М1М2. в отношении 
, если 
 |
Точка М делит отрезок М1М2 в отношении 
.
Точка N делит тот же отрезок М1М2 в отношении 
.
Видимо, при 
мы получим середину отрезка.
Если известны координаты начала М1 и конца М2 отрезка, то координаты точки М, делящей отрезок М1М2 в отношении , находят по формулам:
, 
,
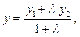
где т. М1(х1, у1, z1), т. М2(х2, у2, z2), т. М(х, у, z).
Координаты середины отрезка получают при :
Например, если т. А(-2, 3, 4), т. В(0, 1, -2), то координаты середины отрезка АВ получим из формул:
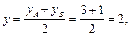
z= 
Итак, точка С(-1, 2, 1) является серединой отрезка АВ.
3. Угол между векторами вычисляется по формуле
cos 
.
4. Условие перпендикулярности двух векторов: х1×х2+у1×у2+z1×z2=0.
5. Условие коллинеарности двух векторов: 
Если векторы коллинеарны, то их соответствующие координаты пропорциональны.
Пример № 1.
Даны три вершины параллелограмма: А(4;2), В(5;7), С(-3;4). Найти четвертую вершину D, противолежащую вершине В.
Для решения этой задачи воспользуемся свойством диагоналей параллелограмма: диагонали его, пересекаясь, делятся точкой пересечения пополам.
Пусть точка М – точка пересечения диагоналей параллелограмма АВСD.
Тогда точка М – середина отрезка АС; координаты точки М найдем из формул:
|
Итак, т. М(
.
Но точка М является серединой и отрезка ВD. Поэтому верны равенства:
и 
.
; 
.
Из этих равенств находим координаты вершины D(-4, -1).
 |
Проверить правильность решения можно, построив все вершины параллелограмма.
Пример № 2.
Найти центр тяжести треугольника, зная координаты его вершин:
А(1;4), В(-5;0), С(-2;-1).
Центр тяжести треугольника лежит в точке пересечения медиан, которая делит отрезок любой медианы в отношении 2:1, считая от вершины.
Точка М делит отрезок СD в отношении =2, а точка D – середина стороны АВ.
; 
Середина стороны АВ – точка D(-2;2). Координаты точки М найдем, рассматривая отрезок СD.
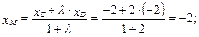
Итак, центр тяжести треугольника лежит в точке М(-2,1).
Построим все точки и убедимся, что решение верно.
Пример № 3.
Проверить, что четырехугольник, вершины которого находятся в точках А(5; 2; 6;), В(6; 4; 4), С(4; 3; 2) и D (3; 1; 4), есть квадрат.
Квадратом является четырехугольник, у которого стороны взаимно перпендикулярны и длины сторон равны.
Запишем координаты векторов, совпадающих со сторонами:
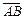=(6-5; 4-2; 4-6)=(1; 2; -2)
=(4-6; 3-4; 2-4)=(-2; -1; -2)
=(3-4; 1-3; 4-2)=(-1; -2; 2)
=(5-3; 2-1; 6-4)=(2; 1; 2)
Проверим, выполняется ли условие перпендикулярности для каждой пары смежных сторон-векторов.
=1×(-2)+2×(-1)+(-2)×(-2)=-2–2+4=0, что и доказывает, что ^ .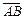
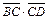=(-2)×(-1)+(-1)×(-2)+(-2)×2=2+2–4=0, т. е. ^ .
=(-1)×2+(-2)×1+2×2=0, т. е. ^ .
=2×1+1×2+2×(-2)=0, т. е. ^ .
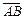Мы установили, что стороны четырехугольника взаимно перпендикулярны. Покажем, что и длины сторон его равны.
,
Итак, АВСD – квадрат. Заметим, что построением эту задачу не проверить, так как точки заданы не на плоскости, а в пространстве.
