«адача 1. Ќайти длину волны де Ѕройл€ дл€ электрона, кинетическа€ энерги€ которого равна:
1) 10 кэ¬, 2) 1 ћэ¬.
| ƒано: | 
|
| Ќайти: | 
|
–ешение: ƒлина волны де Ѕройл€ св€зана с импульсом:
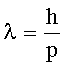
где  - посто€нна€ ѕланка;
- посто€нна€ ѕланка;
р - импульс частицы.
»мпульс частицы зависит от ее скорости. ≈сли скорость движени€ частицы много меньше скорости света в вакууме (v<<c), то это случай нерел€тивистский. ≈сли скорость движени€ частицы соизмерима со скоростью света в вакууме, то это случай рел€тивистский. »мпульс частицы св€зан с энергией. ѕоэтому, чтобы вы€снить, какой это случай, вычислим энергию поко€ частицы и сравним ее с энергией движущейс€ частицы. ¬ычислим энергию поко€ электрона:

—равним кинетическую энергию электрона с энергией поко€ E0. ¬ первом случае W1<<E0, значит это случай нерел€тивистский и импульс равен: p = mv. »мпульс св€зан с кинетической энергией соотношением:

ќтсюда: 
“огда:

¬о втором случае  , значит это случай рел€тивистский. »мпульс равен:
, значит это случай рел€тивистский. »мпульс равен:  , где с - скорость света. “огда:
, где с - скорость света. “огда:

ќтвет:  ,
, 
«адача 2. „астица находитс€ в бесконечно глубокой одномерной потенциальной €ме шириной l на втором энергетическом уровне. ¬ каких точках €мы плотность веро€тности обнаружени€ частицы совпадает с классической плотностью веро€тности?
| ƒано: | 
|
| Ќайти: | x. |
–ешение: ¬олнова€ функци€ ψ, описывающа€ состо€ние частицы в бесконечно глубокой одномерной потенциальной €ме шириной l, имеет вид:
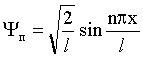 (1)
(1)
где n - номер энергетического уровн€ (n = 1,2,3...),
х - координата частицы в €ме (0 ≤ х ≤ l).
—огласно физическому смыслу волновой функции:
 (2)
(2)
где w - плотность веро€тности обнаружени€ частицы в точке с координатой х.
≈сли частица находитс€ на втором энергетическом уровне (n = 2), т.е.:
 (3)
(3)
¬ыражение дл€ классической плотности веро€тности имеет вид:
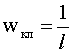 (4)
(4)
ѕриравнива€ по условию выражени€ (3) к (4), получим:
 (5)
(5)
–еша€ уравнение (5), найдем:

¬ пределах €мы (0 ≤ х ≤ l) таких точек четыре:

ќтвет: 
«адача 3. Ќекоторый примесный полупроводник имеет решетку типа алмаза и обладает только дырочной проводимостью. ќпределить концентрацию дырок nр и их подвижность uр, если посто€нна€ ’олла Rх = 3,8Ј10-4 м3/ л. ”дельна€ проводимость полупроводника σ =110 (ќмЈм)-1.
| ƒано: | 
|
| Ќайти: | nр, uр. |
–ешение: онцентраци€ дырок nр св€зана с посто€нной ’олла, котора€ дл€ полупроводников с решеткой типа алмаза, обладающих носител€ми только одного знака, выражаетс€ формулой:
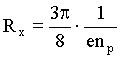 (1)
(1)
где е - элементарный зар€д.
ќтсюда:
 (2)
(2)
ѕодставим числовые значени€ величин в формулу (2) и проведем вычислени€:

”дельна€ проводимость полупроводников выражаетс€ формулой:
 (3)
(3)
где nn и np - концентрации электронов и дырок,
un и up - их подвижности.
ѕри отсутствии электронной проводимости первое слагаемое в скобках равно нулю, и формула (3) примет вид:
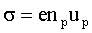
ќтсюда искома€ подвижность:
|
|
|
 (4)
(4)
ѕодставим в (4) выражение nр, описываемое формулой (2):
 (5)
(5)
ѕодставим в (5) численные значени€ и проведем вычислени€:

ќтвет:  ,
, 






