‘изические основы механики
ѕо€снение к рабочей программе
‘изика, нар€ду с другими естественными науками, изучает объективные свойства окружающего нас материального мира. ‘изика исследует наиболее общие формы движени€ материи. ѕростейшей и наиболее общей формой движени€ €вл€етс€ механическое движение. ћеханическим движением называетс€ процесс изменени€ взаимного расположени€ тел в пространстве и с течением времени.
лассическа€ механика изучает движение макроскопических тел, совершаемых со скорост€ми, малыми по сравнению со скоростью света в вакууме. «аконы классической механики были сформулированы ». Ќьютоном в 1687 году, но не утратили своего значени€ в наши дни. ƒвижение частиц со скорост€ми пор€дка скорости света рассматриваетс€ в рел€тивистской механике, основанной на специальной теории относительности, а движени€ микрочастиц изучаетс€ в квантовой механике. Ёто значит, что законы классической механики имеют определенные границы применени€.
ћеханика делитс€ на три раздела: кинематику, динамику и статику. ¬ разделе кинематика рассматриваютс€ такие кинематические характеристики движени€, как перемещение, скорость, ускорение. «десь необходимо использовать аппарат дифференциального и интегрального исчислени€. ¬ контрольной работе - это задачи 101-110.
¬ основе классической динамики лежат три закона Ќьютона. «десь необходимо обратить внимание на векторный характер действующих на тела сил, вход€щих в эти законы (задачи 111-120).
ƒинамика охватывает такие вопросы, как закон сохранени€ импульса (задачи 121-130), закон сохранени€ полной механической энергии, работа силы (задачи 131-140).
ѕри изучении кинематики и динамики вращательного движени€ следует обратить внимание на св€зь между угловыми и линейными характеристиками. «десь ввод€тс€ пон€ти€ момента силы, момента инерции, момента импульса и рассматриваетс€ закон сохранени€ момента импульса (задачи 141-160).
ќсновные формулы
—корость мгновенна€: где  - радиус-вектор материальной точки, t - врем€; - радиус-вектор материальной точки, t - врем€;  - производна€ радиус-вектора материальной точки по времени. - производна€ радиус-вектора материальной точки по времени.
| 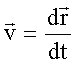
|
| ћодуль вектора скорости: где s - рассто€ние вдоль траектории движени€ (путь) | 
|
| —корость средн€€ (модуль): |  
|
| ”скорение мгновенное: | 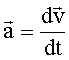
|
| ћодуль вектора ускорени€ при пр€молинейном движении: | 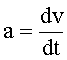
|
| ”скорение при криволинейном движении: нормальное где R - радиус кривизны траектории, тангенциальноеполное (вектор)(модуль) |    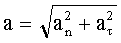
|
| —корость и путь при движении: равномерномравнопеременном V0- начальна€ скорость; а > 0 при равноускоренном движении; а < 0 при равнозамедленном движении. |  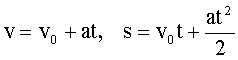
|
| ”глова€ скорость: где φ - угловое перемещение. | 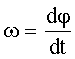
|
| ”гловое ускорение: | 
|
| —в€зь между линейными и угловыми величинами: | 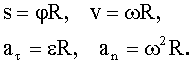
|
| »мпульс материальной точки: где m - масса материальной точки. | 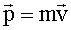
|
ќсновное уравнение динамики поступательного движени€ (II закон Ќьютона): где 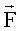 - результирующа€ сила, - результирующа€ сила,  <> <>
| 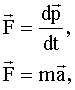
|
| ‘ормулы сил: т€жести где g - ускорение свободного падени€ трени€ где μ - коэффициент трени€, N - сила нормального давлени€, упругости где k - коэффициент упругости (жесткости), Δх - деформаци€ (изменение длины тела). | 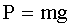 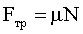 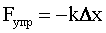
|
«акон сохранени€ импульса дл€ замкнутой системы, состо€щей из двух тел: где  - скорости тел до взаимодействи€; - скорости тел до взаимодействи€; 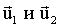 - скорости тел после взаимодействи€. - скорости тел после взаимодействи€.
| 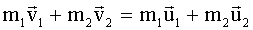
|
| ѕотенциальна€ энерги€ тела: подн€того над «емлей на высоту hупругодеформированного | 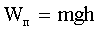 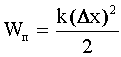
|
| инетическа€ энерги€ поступательного движени€: | 
|
| –абота посто€нной силы: где α - угол между направлением силы и направлением перемещени€. | 
|
| ѕолна€ механическа€ энерги€: | 
|
| «акон сохранени€ энергии: силы консервативнысилы неконсервативны где W1 - энерги€ системы тел в начальном состо€нии; W2 - энерги€ системы тел в конечном состо€нии. |  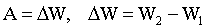
|
| ћомент инерции тел массой m относительно оси, проход€щей через центр инерции (центр масс): тонкостенного цилиндра (обруча) где R - радиус, сплошного цилиндра (диска)шарастержн€ длиной l, если ось вращени€ перпендикул€рна стержню и проходит через его середину | 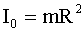 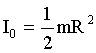 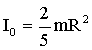 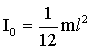
|
ћомент инерции тела относительно произвольной оси (теорема Ўтейнера): где  - момент инерции тела относительно оси, проход€щей через центр масс, d - рассто€ние между ос€ми. - момент инерции тела относительно оси, проход€щей через центр масс, d - рассто€ние между ос€ми.
| 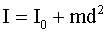
|
| ћомент силы(модуль): где l - плечо силы. | 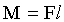
|
ќсновное уравнение динамики вращательного движени€: где 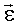 - угловое ускорение, - угловое ускорение, 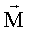 - результирующий момент сил. - результирующий момент сил.
| 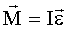
|
| ћомент импульса: материальной точки относительно неподвижной точки где r - плечо импульса, твердого тела относительно неподвижной оси вращени€ |  
|
«акон сохранени€ момента импульса: где 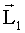 - момент импульса системы в начальном состо€нии, - момент импульса системы в начальном состо€нии, 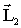 - момент импульса системы в конечном состо€нии. - момент импульса системы в конечном состо€нии.
| 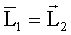
|
| инетическа€ энерги€ вращательного движени€: | 
|
| –абота при вращательном движении где Δφ - изменение угла поворота. | 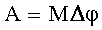
|
|
|
|
ѕримеры решени€ задач по механике
«адача 1. ƒвижение тела массой 2 кг задано уравнением: 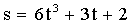 , где путь выражен в метрах, врем€ - в секундах. Ќайти зависимость ускорени€ от времени. ¬ычислить равнодействующую силу, действующую на тело в конце второй секунды, и среднюю силу за этот промежуток времени.
, где путь выражен в метрах, врем€ - в секундах. Ќайти зависимость ускорени€ от времени. ¬ычислить равнодействующую силу, действующую на тело в конце второй секунды, и среднюю силу за этот промежуток времени.
| ƒано: | 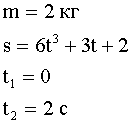
|
| Ќайти: | 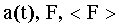
|
–ешение: ћодуль мгновенной скорости находим как производную от пути по времени:
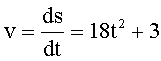
ћгновенное тангенциальное ускорение определ€етс€ как производна€ от модул€ скорости по времени:
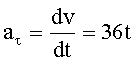
—реднее ускорение определ€етс€ выражением:
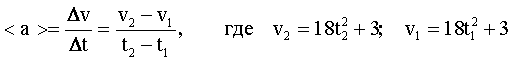
ѕосле подстановки:
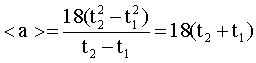
–авнодействующа€ сила, действующа€ на тело, определ€етс€ по второму закону Ќьютона:

“огда
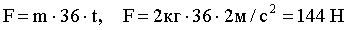
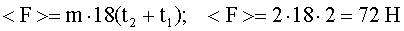
ќтвет: a(t) = 36t, F = 144 H, = 72 H.
«адача 2. ѕо наклонной плоскости, составл€ющей с горизонтом угол 30º, движетс€ тело массой 5 кг. этому телу с помощью нераст€жимой нити, перекинутой через блок, прив€зано тело такой же массы, движущеес€ вертикально вниз (рис. 1). оэффициент скольжени€ между телом и наклонной плоскостью 0,05. ќпределить ускорение тел и силу нат€жени€ нити.
| ƒано: | 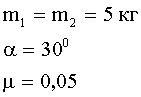
|  –ис. 1
–ис. 1
|
| Ќайти: | 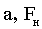
|
–ешение: ѕокажем на рисунке силы, действующие на каждое тело. «апишем дл€ каждого из тел уравнение движени€ (второй закон Ќьютона):
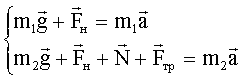
¬ проекци€х на выбранные оси координат:

”читыва€, что 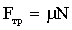 , где
, где 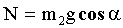 , получим систему уравнений:
, получим систему уравнений:
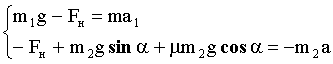
¬ычтем из первого уравнени€ второе:
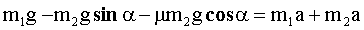
»скомое ускорение равно:
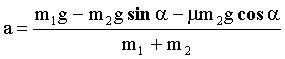
|
|
|
¬ычислим ускорение а:

—илу нат€жени€ найдем из первого уравнени€ системы:
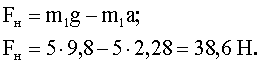
ќтвет: 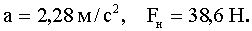
«адача 3. Ќайти линейные ускорени€ движени€ центров т€жести шара и диска, скатывающихс€ без скольжени€ с наклонной плоскости. ”гол наклона плоскости равен 30º. Ќачальна€ скорость тел равна нулю.
| ƒано: | 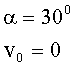
| 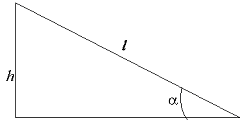 –ис. 2
–ис. 2
|
| Ќайти: | 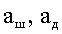
|
–ешение: ѕри скатывании тела с наклонной плоскости высотой h его потенциальна€ энерги€ переходит в кинетическую поступательного и вращательного движени€. ѕо закону сохранени€ энергии:
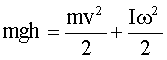 (1)
(1)
где I - момент инерции тела, m - масса.
ƒлина наклонной плоскости l св€зана с высотой соотношением (рис. 2):
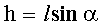 (2)
(2)
Ћинейна€ скорость св€зана с угловой:
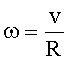 (3)
(3)
ѕосле подстановки (2) и (3) в (1), получим:
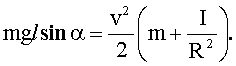 (4)
(4)
“ак как движение происходит под действием посто€нной силы (силы т€жести), то движение тел - равноускоренное. ѕоэтому:
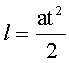 (5)
(5)
и
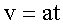 (6)
(6)
–еша€ совместно (4), (5) и (6), получим:
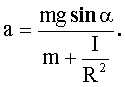 (7)
(7)
ћоменты инерции:
| дл€ шара: | 
|
| дл€ диска: | 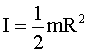
|
ѕодставл€€ выражение дл€ момента инерции в формулу (7), получим:
| дл€ шара: | 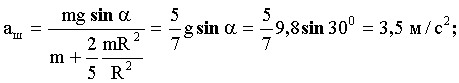
|
| дл€ диска: | 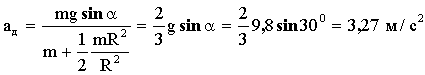
|
ќтвет: 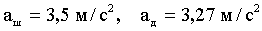
Ёлектричество и магнетизм






