В инерционной системе значение процесса на выходе y (t) зависит не только от значения процесса x (t), действующего на входе в тот же момент времени, но и от его значений в предшествующие моменты времени. Следовательно, процесс на выходе линейной инерционной системы будет представлять собой суперпозицию откликов на все воздействия в интервале от нуля до t включительно. Эта суперпозиция характеризуется известным интегралом Дюамеля
, (6)
где 
- значение процесса на входе в момент времени τ;
- импульсная характеристика системы, т.е. ее отклик на импульсное
воздействие в виде δ -функции;
t - момент наблюдения процесса на выходе;
τ - момент начала действия (приложения) процесса на входе.
Для линейных систем с постоянными параметрами импульсная характеристика зависит только от (t -τ), т. е. g (t, τ) = g (t- τ). В этом случае
. (7)
Импульсная характеристика и коэффициент передачи линейной инерционной системы связаны между собой парой преобразований Фурье:
(8)
Энергетический спектр случайного процесса на выходе линейной
инерционной системы определяется выражением
(9)
Пусть, например, белый шум с равномерной спектральной плотностью мощности 
воздействует на интегрирующую RC -цепь, для которой
. (10)
Тогда
.
Корреляционная функция на выходе линейной инерционной системы
является преобразованием Фурье от энергетического спектра 
. (11)
Сложной задачей является определение функции распределения процесса на выходе линейной инерционной системы. Только в частном случае, когда x (t) является гауссовским процессом с нормальным законом распределения вероятностей мгновенных значений, процесс на выходе y (t) также остается гауссовским, но при этом изменяются его числовые характеристики.
Характерной особенностью линейных инерционных систем является свойство "нормализации" процесса на их выходе (при определенных условиях). Оно заключается в том, что распределение процесса на выходе достаточно хорошо аппроксимируется нормальным законом, независимо от того, какое распределение процесс имел на входе. Такое явление возможно лишь при условии, когда длительность переходных процессов линейной инерционной цепи велика по сравнению со скоростью изменения процесса на входе. Физически это объясняется тем, что отдельные отклики на выходе, вызванные хаотическими воздействиями входного процесса, не успевают затухать (инерционность цепи), накладываются друг на друга и образуют новый случайный процесс (суперпозиция). А согласно центральной предельной теоремы теории вероятностей (теорема Ляпунова) закон распределения этого процесса, представляющего собой сумму большого числа независимых случайных величин (откликов), стремится к нормальному закону распределения вероятностей.
Длительность переходных процессов 
радиотехнической цепи
однозначно определяется ее полосой пропускания примерным соотношением
. В свою очередь скорость изменения процесса на входе цепи будет определяться шириной его энергетического спектра, – чем быстрее изменяется процесс, тем шире его спектр. Следовательно, явление "нормализации" будет иметь место только на выходе узкополосных линейных инерционных цепей, т.е. таких, у которых полоса пропускания много меньше, чем ширина энергетического спектра процесса на входе.
В качестве примера рассмотрим прохождение смеси синусоидального
колебания 
с гауссовским случайным процессом через типовое
радиотехническое устройство: узкополосный усилитель – линейный амплитудный детектор – фильтр нижних частот. Распределение мгновенных значений y (t) на выходе узкополосной системы будет нормальным с математическим ожиданием 
, а его огибающая 
(после амплитудного детектора) будет иметь обобщенное распределение Релея (см. рисунок 1,
кривые б и в)
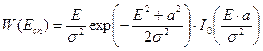. (12)
В отсутствие синусоидального сигнала (a = 0) огибающая узкополосного гауссовского процесса будет иметь простое распределение Релея (рисунок 1, кривая а)
. (13)
