Приложение 8.1
ПРОХОЖДЕНИЕ СЛУЧАЙНЫХ СИГНАЛОВ
ЧЕРЕЗ ЛИНЕЙНЫЕ И НЕЛИНЕЙНЫЕ УСТРОЙСТВА
Обшие сведения
Типовые задачи, связанные с преобразованием случайных процессов
радиотехническими устройствами, можно разбить на две группы:
1 Определение функций распределения выходного случайного процесса (общая задача).
2 Определение числовых характеристик процесса на выходе устройства.
Очевидно, что решение задач второй группы в общем случае может быть получено на основе результатов задач первой группы.
В большинстве случаев элементы радиотехнических устройств необходимо рассматривать как нелинейные инерционные. Однако, анализ прохождения случайных сигналов через радиотехнические устройства при столь общих предположениях связан со значительными математическими трудностями, так как в этом случае используются нелинейные дифференциальные уравнения
со случайными коэффициентами.
С учетом степени сложности анализа преобразования случайных сигналов радиотехнические цепи подразделяются на нелинейные безынерционные, линейные инерционные, параметрические, нелинейные инерционные. Так, например, амплитудный детектор можно рассматривать как последовательное соединение нелинейного безынерционного элемента (выпрямительного диода) и линейного инерционного в виде нагрузки (селективного RC фильтра). Таким образом, полное преобразование сигнала в амплитудном детекторе является результатом двух преобразований: нелинейного безынерционного и линейного инерционного
Нелинейные безынерционные устройства
Нелинейное преобразование называют безынерционным (или функциональным), если значение выходного процесса y (t)(отклик) в любой момент времени определяется только значением входного процесса x (t) (воздействие) в тот же момент времени и не зависит от его значений в предшествующие моменты времени. Такое функциональное преобразование имеет место, например, при ограничении, модуляции, преобразовании частоты, детектировании и т. д.
Характеристика нелинейного безынерционного элемента задается в виде функционального соотношения
 (1)
(1)
Функция распределения процесса на выходе для таких цепей определяется для заданной плотности распределения воздействия по известному правилу функционального преобразования случайных величин (процессов). Числовые характеристики процесса на выходе нелинейных безынерционных устройств можно определить без знания его плотности распределения W (y) по известным W (x) и функциональной зависимости y=f (x). Можно показать, что они будут
определяться следующими выражениями:
математическое ожидание
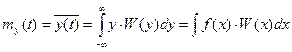 , (2)
, (2)
дисперсия
 , (3)
, (3)
корреляционная функция
 . (4)
. (4)
Соответственно
 . (5)
. (5)
Таким образом, при воздействии случайного процесса на нелинейную систему изменяются на ее выходе спектр процесса, закон распределения вероятностей и все связанные с ними параметры процесса.






