Зависимость балансовой прибыли и ежегодной суммы амортизации.

Ежегодная сумма амортизации, млн.руб.	Число предприятий, fi	åyi	Средняя величина балансовой прибыли, млн.руб.,
30 – 34			156,0
34 – 38			165,4
38 – 42			169,3
42 – 46			173,7
Итого:			–

Как видно из данных групповой таблицы 10.3 с увеличением годовой суммы амортизации возрастает величина балансовой прибыли. На рис. 10.1 представлен график связи.

Рис. 10.1. Зависимость балансовой прибыли от ежегодной суммы амортизации.

Эмпирическая линия связи приближается к прямой линии. Следовательно, можно считать наличие прямолинейной корреляции.

1. Для измерения степени тесноты связи используется линейный коэффициент корреляции:

 

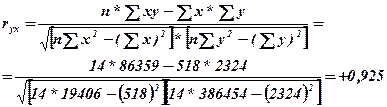
Для расчета коэффициента корреляции была использована вспомогательная таблица 10.4:

 

Таблица 10.4.

№ предприя-тия	Сумма аморти-зации, млн.руб., х	Балансовая прибыль, млн. руб., у	х2	у2	ху	ут	у-ут	(у-ут)2
						163,0	-1,0	1,00
						170,5	+3,5	12,25
						155,5	-0,5	0,25
						173,5	-1,5	2,25
							+7,0	49,00
						167,5	-1,5	2,25
						161,5	+0,5	0,25
						160,0	0,0	0,00
						164,5	+2,5	6,25
						157,0	-4,0	16,00
						164,5	-1,5	2,25
						175,0	-2,0	4,00
						169,0	-1,0	1,00
						176,5	-0,5	0,25
Итого						–	–	97,00

 

Значение линейного коэффициента корреляции (r=+0,925) свидетельствует о наличии прямой и очень тесной связи.

Средняя квадратическая ошибка коэффициента корреляции:

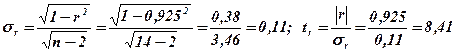
Далее необходимо сравнить расчетное значение t -критерия с табличным, которое определяется по таблице значений t -критерия Стьюдента в зависимости от k степеней свободы и заданного уровня значимости[1].

Согласно таблице, t -критерий Стьюдента при уровне значимости 95% и числе степеней свободы k=14-2=12 составит 2,179.

Так как расчетное значение t_r=8,41>2,179, можно утверждать значимость коэффициента корреляции.

 

1. Определяем модель связи. График линии средних показывает наличие линейной связи, поэтому используется функция .

 

Определим коэффициенты уравнения, используя следующие формулы:

 

Таким образом, модель связи следующая:

Для возможности использования линейной функции определяется величина , которая оценивает возможность использования подобранной функции в качестве модели, характеризующей изучаемое явление.

Для расчета теоретического значения F -критерия исчисляется корреляционное отношение (по данным табл. 10.4):

Следовательно, корреляционное отношение показывает наличие достаточно тесной связи.

 

Определим F -критерий:

 

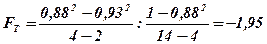
При вероятности 95%, числе степеней свободы k₁=m-2=4-2=2 и k₂=n-m=14-4=10, табличное значение F=4,10. Так как расчетное значение меньше табличного, то возможность использования линейной функции не опровергается.

Средняя квадратическая ошибка уравнения:

где у_т – значения результативного признака, рассчитанные по уравнению связи.

Так для предприятия №1 у_т=110,5+1,5*35=163; для остальных предприятий расчет выполняется аналогично. Результаты расчета представлены в табл. 10.4.

Для оценки взаимосвязи двух признаков необходимо рассчитать коэффициент аппроксимации:

Полученный коэффициент аппроксимации значительно меньше 15%, поэтому уравнение достаточно хорошо отображает взаимосвязь двух признаков и может быть использовано в практической работе.

Задачи

 

10.1. Зависимость между объемом реализованной продукции и балансовой прибылью по 10 предприятиям одной из отраслей промышленности характеризуется следующими данными:

 

№ предприятия	Объем реализованной продукции, млн.руб.	Балансовая прибыль, млн.руб.
	491,8	133,8
	483,0	124,1
	481,7	62,4
	478,7	62,9
	478,9	51,4
	475,2	72,4
	474,4	99,3
	459,5	40,9
	452,9	104,0
	446,5	116,1

Определите вид корреляционной зависимости, постройте уравнение регрессии, рассчитайте параметры уравнения, вычислите тесноту связи.

 

10.2. По данным задачи 3.1. (тема: Сводка и группировка) постройте зависимость между суммой активов и величиной балансовой прибыли, рассчитайте коэффициент корреляции и определите тесноту связи.

 

10.3. Имеются следующие данные:

№ предприятия	Объем продукции, млн.руб.	Стоимость основного капитала, млн.руб.	Чистый доход, млн.руб.	Численность, чел.
	507,2		352,9
	506,6		187,1
	487,8		375,2
	496,0		287,9
	493,6		444,0
	458,9		462,4
	429,3		459,5
	386,9		511,3
	311,5		328,6
	302,2		350,0
	262,0		298,7
	242,4		529,3
	231,9		320,0
	214,3		502,0
	208,4		194,9

Составьте линейное уравнение регрессии зависимости чистого дохода от стоимости основного капитала. Дайте характеристику тесноты и направления связи между признаками.

 

10.4. По данным задачи 3.1 (тема: Сводка и группировка) постройте зависимость между величиной собственного капитала и величиной балансовой прибыли. Рассчитайте коэффициент корреляции и определите тесноту связи. Проверьте аналитическое выражение связи на достоверность.

 

10.5. Используя данные задачи 10.3, определите вид корреляционной зависимости между объемом производства и стоимостью основного капитала. Постройте линейное уравнение регрессии, вычислите параметры уравнения, рассчитайте коэффициент корреляции и корреляционное отношение. Сравните величину коэффициента корреляции и корреляционного отношения. Проверьте аналитическое выражение связи на достоверность. Сделайте выводы.

 

10.6. По данным задачи 10.3 определите вид корреляционной зависимости между показателями чистого дохода и численностью персонала. Найдите параметры уравнения регрессии, определите направление и тесноту связи. Проверьте аналитическое выражение связи на достоверность.

 

10.7. Для выявления зависимости производительности труда рабочих, выполняющих в цехе операцию, от стажа их работы был найден линейный коэффициент корреляции, равный 0,8. Кроме того, известны следующие данные:

• средний стаж работы рабочих 5 лет;
• среднее квадратическое отклонение по стажу 2 года;
• среднее квадратическое отклонение по производительности труда 4,4 шт.;
• коэффициент вариации по производительности труда 40%.

Найдите аналитическое уравнение связи, характеризующее зависимость производительности труда рабочих от стажа их работы.

 

10.8. По 20 однородным предприятиям была получена модель, отражающая зависимость выпуска продукции (у) за месяц от размера основного капитала (х): .

Кроме того, по этой совокупности известны следующие данные:

• средняя стоимость основного капитала на одно предприятие 12 млн.руб.;
• средний размер выпуска продукции на одно предприятие 18 млн.руб.;
• среднее квадратическое отклонение по стоимости основного капитала 3,5 млн.руб.;
• среднее квадратическое отклонение по размеру выпуска продукции 2 млн.руб.

Определите степень тесноты связи между размером выпуска продукции и стоимостью основного капитала, учитывая форму связи и используя для этого приведенные данные.

 

Рекомендуемая литература

Рекомендовано Министерством образования РФ

 

1. Громыко Г.Л. Статистика. Практикум. – М.: Инфра-М, 2003.

2. Гусаров В.М. Теория статистики: Учеб. Пособие для ВУЗа. – М.: Аудит, ЮНИТИ, 1998.

3. Ефимова М.Р. Общая теория статистики. – М.: Финансы и статистика, 2001.

4. Ефимова М.Р. Практикум по общей теории статистики. – М.: Финансы и статистика, 2005.

5. Практикум по статистике / Под ред. Симчеры В.М., – М.: Финстатинформ, 1999.

6. Практикум по теории статистики / Под ред. Шмойловой Р.А., – М.: Финансы и статистика, 2004.

7. Сборник задач по общей теории статистики / Под ред. Глинского Н.Н. – М.: Инфра-М, 2002.

8. Статистика / Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2003.

9. Статистика. Курс лекций / Под ред. Ионина И.Г.- М.: Инфра-М, Новосибирск: изд-во НГУ, 2002.

10. Теория статистики / Под ред. Шмойловой Р.А., – М.: Финансы и статистика, 2004.

[1] Таблицы значений t-критерия Стьюдента можно найти в рекомендованных учебниках по теории статистики.