Задача. Имеются данные по восьми фирмам о часовой оплате труда х и уровне текучести кадров у. Необходимо измерить тесноту связи между х и у.
Расчетная таблица для определения линейного коэффициента корреляции
| № п/п | Часовая оплата труда, руб. х | Уровень текучести кадров, % у | х2 | ху | у2 |
| Σ | |||||
| Средняя величина | 
| 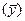
| 
| 
| 
|
Предположив линейную зависимость между ними, сначала рассчитаем σx и σy:
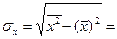

Линейный коэффициент корреляции:

Таким образом, получен результат: r = ______, что позволяет сделать вывод о том, что между оплатой труда х и уровнем текучести кадров у существует сильная ________ связь, т.е. с увеличением оплаты труда текучесть кадров снижается.
Проверка коэффициента корреляции на значимость (существенность)
Интерпретируя значение коэффициента корреляции, следует иметь в виду, что он рассчитан для ограниченного числа наблюдений и подвержен случайным колебаниям, как и сами значения х и у, на основе которых он рассчитан, т.е., как любой выборочный показатель, он содержит случайную ошибку и не всегда однозначно отражает действительно реальную связь между изучаемыми показателями.
Для того чтобы оценить существенность (значимость) самого r и, соответственно, реальность измеряемой связи между х и у, необходимо рассчитать среднюю квадратическую ошибку коэффициента корреляции σr.
Оценка существенности (значимости) линейного коэффициента корреляции основана на сопоставлении значения r с его средней квадратической ошибкой:

Укажем особенности расчета этого критерия в зависимости от числа наблюдений (объема выборки) – n.
1. Если число наблюдений достаточно велико (n > 50) и есть основания полагать, что выборка осуществлена из нормальной совокупности, то средняя ошибка коэффициента корреляции рассчитывается по следующей приближенной формуле:
 .
.
Обычно при большом n, если коэффициент корреляции r превышает свою среднюю ошибку σr. больше чем в 3 раза, т.е.

он считается значимым (существенным), а связь - реальной. Задавшись определенной вероятностью, можно определить доверительные пределы (границы) r. Так, при вероятности 0,95, для которой коэффициент доверия t = 1.96, доверительные границы r составят:

При вероятности 0,997, для которой коэффициент доверия t = 3, доверительные границы r составят:

Поскольку значение r не может превышать единицу, то в случае, если  следует указывать только нижний предел, т.е. утверждать, что реальный r не менее чем
следует указывать только нижний предел, т.е. утверждать, что реальный r не менее чем 
2. При небольшом числе наблюдений (n < 30) средняя ошибка линейного коэффициента корреляции определяется как:

а значимость r проверяется на основе t- критерия Стьюдента. При этом выдвигается и проверяется нулевая гипотеза о равенстве коэффициента корреляции нулю, т.е. гипотеза об отсутствии связи между х и у в генеральной совокупности. Для этого определяется расчетное значение критерия:

и сопоставляется с tтабл.
Если нулевая гипотеза верна, т.е. r = 0, то распределение t- критерия подчиняется закону Стьюдента (с заданными параметрами: уровнем значимости α, принимаемым обычно за 0,05, и числом степеней свободы v = n – 2). Поэтому в каждом конкретном случае по таблице распределения t- критерия Стьюдента находится критическое значение t, которое допустимо при справедливости нулевой гипотезы, и с ним сравнивается фактическое (расчетное) значение t.
Если tрасч>tтабл, то нулевая гипотеза отвергается и линейный коэффициент считается значимым, а связь между х и у - реальной.
Если tрасч<tтабл, то нулевая гипотеза не отвергается и коэффициент корреляции считается незначимым, т.е. считается, что связь между х и у отсутствует, и значение r отличное от нуля, получено случайно.
Проверим на значимость рассчитанный в нашем случае линейный коэффициент корреляции. Так как n = 8, r = ______, средняя ошибка коэффициента корреляции:
 Отсюда:
Отсюда: 
По таблице находим (при α = 0,05 и числе степеней свободы v = 8 – 2 = 6: tтабл = 2.4469).
Так как полученное tрасч =______ > tтабл = 2,4469, то нулевая гипотеза об отсутствии связи между х и у в генеральной совокупности отвергается, т.е. мы делаем вывод, что коэффициент корреляции значим и существенно отличается от нуля, подтверждая тем самым реальную связь между х и у.
Список литературы
1. Башкатов Б.И. Статистика сельского хозяйства с основами общей теории статистики: Курс лекций. – М.: ТАНДЕМ, 2001.
2. Годин А.М. Статистика: Учебник. – 2-е изд., перераб. – М.: Изд. торг. корпорация «Дашков и К», 2004.
3. Елисеева И.И., Юзбашев М.М. Общая теория статистики: Учебник /Под ред. И.И. Елисеевой. – 5-изд., перераб и доп. - М.: Финансы и статистика, 2006.
4. Зинченко А.П. Сельскохозяйственная статистика с основами социально-экономической статистики: Учебник. - М.: Изд-во МСХА, 1998.
5. Практикум по статистике: Учебное пособие. Зинченко А.П., Шибалкин А.Е., Тарасова О.Б., Шайкона Е.В. - М.: Колос, 2001.
6. Статистика: учебник /И.И. Елисеева [и др.]; под ред. И.И. Елисеевой. – М.: ТК Велби, Изд-во Проспект, 2006.
7. Статистика: Учебник /Под ред. проф. И.И. Елисеевой. – М.: ПРОСПЕКТ, 2003.
8. Экономическая статистика. Учебник. Иванов Ю.Н., Казарина С.Е., Громыко Г.Л. и др. - М.: ИНФРА-М, 2006. - 736 с.
9. Теория статистики /Под ред. Р.А. Шмойловой. - М.: Финансы и статистика, 2002.
Составитель Шелковников Сергей Александрович
СТАТИСТИКА
Методические указания
Компьютерная верстка Харченко Е.В.
Подписано к печати 05.03.2008 г.
Объем 1,45 п.л. Формат 84 x 108/32. Тираж 100 экз. Изд. №10.
Отпечатано в типографии Экономического института
630039, Новосибирск, ул. Никитина, 155






