| Номер группы банков | Собственный капитал, млн р. | Удельный вес банков dj, % | Средняя величина привлеченных средств  , млн руб.
| Дисперсия привлеченных средств σj2 |
| 200-300 | ||||
| 300-400 | ||||
| 400-500 | ||||
| 500-600 | ||||
| Итого | - | - | - |
Определить показатели тесноты связи между величиной собственных средств и привлеченными капиталами.
Показателями тесноты связи являются:
Средний размер привлеченных средств по всей совокупности банков:
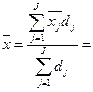
Межгрупповая дисперсия:
Внутригрупповая дисперсия:
Общая дисперсия 
Коэффициент детерминации:
Эмпирическое корреляционное отношение:
Изменение величины собственного капитала влияет на изменение размера привлеченных средств на ________ %. Между показателями существует тесная прямая связь.
Тема 4. Ряды динамики
| Показатели | Цепные | Базисные |
| Абсолютный прирост ∆i | yi - yi-1 | yi - y1 |
| Темп роста (Tp) | yi / yi-1 | yi / y1 |
| Темп прироста (Тп) | Tp – 100% | Tp – 100% |
| Коэффициент опережения (К) |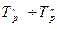 
| |
| Абсолютное значение одного процента прироста – αi | 
| |
Средний абсолютный прирост 
| 
| |
| Средний относительный прирост (коэффициент роста) | 
| |
Средний темп роста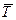 
|  
| |
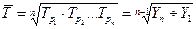
| Средний темп прироста | 
|
В формулах Yi обозначает текущий уровень ряда, y i-1 – предшествующий, Y1 – начальный уровень ряда.
Задача. Рассчитайте цепные и базисные абсолютные приросты, темпы роста и прироста, средний абсолютный прирост, средний темп роста, коэффициенты опережения по элементам рынка ссудных капиталов.
| Виды ставок | I год | II год | III год | IV год |
| Ставка по кредитам | 187,8 | 176,4 | 142,8 | 80,2 |
| Учетная ставка ЦБ | 136,2 | 96,2 | 59,8 |
Произведем расчеты и занесем значения в таблицу.
| Показатели | Ставка по кредитам | Учетная ставка ЦБ |
| ∆i: цепной | ||
| базисный | ||
| Тp: цепной | ||
| базисный | ||
| Тn: цепной | ||
| базисный | ||
|
| ||
|
| ||
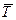
| Коэффициент опережения (К) |
Задача. На основе данных о динамике дефицита федерального бюджета необходимо определить основную тенденцию рассматриваемого показателя.
| Дата | t | Дефицит федерального бюджета у, (в % к общей сумме расходов) | y·t | t2 | 
| 
| 
|
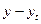
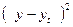
| 1.01. | -4 | ||||||
| 1.02. | -3 | ||||||
| 1.03. | -2 | 16,5 | |||||
| 1.04. | -1 | 19,8 | |||||
| 1.05. | |||||||
| 1.06. | 12,4 | ||||||
| 1.07. | 11,3 | ||||||
| 1.08. | |||||||
| 1.09. | |||||||
| Итого |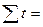 
| 
| 
| 
| 
| – | 
|
1. Исходя из внутригодовой фактической динамики показателя в качестве функции выравнивания выберем уравнение прямой: 
2. Для нахождения параметров уравнения выравнивания решите систему:
Функция выравнивания принимает вид: = ______ - _____ t
3. Найдите выравненные значения функции .
4. Изобразите график фактических данных и тренд.
у, %
20
0
T, время
5. Найдите показатель относительной колеблемости уровней ряда около тренда:
Величина относительной колеблемости уровней ряда около тренда, значение коэффициента вариации, а также графическое изображение фактической динамики дефицита государственного бюджета и тренда показывают, что функция выравнивания достаточно точно воспроизводит фактические данные. Таким образом, дефицит государственного бюджета имел тенденцию к понижению.
Задача. Заключая договор, страхователь уплачивает не нетто-ставку, а брутто-ставку, так как страховая компания должна покрыть расходы на ведение дела и получить прибыль:
Брутто-ставка = Нетто-ставка + Нагрузка.
Нагрузка определяется исходя из затрат, связанных с затратами компании по выполнению своих функций, на базе информации бухгалтерского учета, фактических затрат и стратегии компании на страховом рынке. Если, предположим, 20% общего размера брутто-ставки составляют расходы на ведение дела, комиссионные вознаграждения, прибыль компании, то брутто-ставка будет равна: Нетто-ставка/(1-0,2).
Нетто-ставка в общем виде равна сумме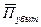 
и рисковой надбавки. Последняя представляет собой допустимую ошибку, взятую с положительным знаком. Расчет рисковой надбавки опирается на законы распределения случайной величины. Для нормального закона распределения можно записать 
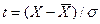, откуда ожидаемая убыточность будет равна 
. Задавая вероятность р, можно определить значение I, воспользовавшись соответствующими таблицами. Отсюда следует, что в общем виде нетто-ставка в имущественном страховании может быть рассчитана по формуле 
.
Важно, чтобы ошибка ожидаемого страхового возмещения не превысила с определенной вероятностью заданных пределов. Вероятность такой ошибки устанавливается страховщиком. Величина ошибки подбирается на основе стратегии компании путем соответствующего значения коэффициента t из таблицы:
| t | 1,6 | |||
| P | 0,683 | 0,9 | 0,954 | 0,997 |
В условиях нестабильной экономики при расчете тарифных ставок в каждом конкретном виде имущественного страхования необходимо учитывать тенденции, складывающиеся в динамике убыточности.
Предположим, что мы располагаем следующими данными:
| Годы | Средние показатели убыточности по отдельным видам страхования на 100 руб. страховой суммы | ||
| вид №1 | вид №2 | вид №3 | |
| 1. | – | – | 28,0 |
| 2. | 30,0 | 20,0 | 31,0 |
| 3. | 32,0 | 23,0 | 31,5 |
| 4. | 34,0 | 28,0 | 37,0 |
| 5. | 35,0 | 31,0 | 39,0 |
| 6. | 36,0 | 28,0 | 43,0 |
| 7. | 38,0 | 30,0 | 48,0 |
| 8. | 39,0 | 32,0 | 55,5 |
| 9. | 40,0 | 32,0 | 61,5 |
| 10. | – | – | 77,0 |
Определите тенденцию, сложившуюся в изменении тарифной ставки по каждому виду страхового продукта. Представьте данные таблицы и полученные результаты графически.
1. По виду страхования №1 показатель убыточности равномерно возрастает, поэтому при расчете нетто-ставки можно опираться на средний показатель убыточности и среднее квадратическое отклонение от нее. Схема расчета имеет следующий вид:
| Годы | Пубыт на 100 руб. страховой суммы, руб. | 
| 
|
|
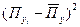
Средний показатель убыточности
______________________________ руб. на 100 руб. страховой суммы.
Определим среднее квадратическое отклонение:
Таким образом, при t = 2 (p = _________) рисковая надбавка:
tσ = ______________ руб.
В этом случае нетто-ставка за 9 год может быть принята в размере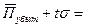 
____________________________ руб.
Исходя из полученных выше значений показатель убыточности равномерно возрастает во времени, поэтому целесообразно учесть данную тенденцию.
Покажите выравнивание показателя убыточности по прямой в таблице и на графике.
| Годы | t | t2 | Пубыт на 100 руб. страховой суммы, руб. | Пyt | 
| 
| 
|
| 1. | 30,0 | ||||||
| 2. | 32,0 | ||||||
| 3. | 34,0 | ||||||
| 4. | 35,0 | ||||||
| 5. | 36,0 | ||||||
| 6. | 38,0 | ||||||
| 7. | 39,0 | ||||||
| 8. | 40,0 | ||||||
|
|
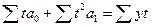
Делим оба уравнения на коэффициенты при а0:
Вычитаем из второго уравнения первое:
На основе рассчитанных коэффициентов получаем уравнение прямой с параметрами:
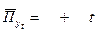
| Показатель убыточности, на 100 руб. страховой суммы | ||||||||||
Используя полученные данные, осуществите прогноз значения показателя убыточности на 9 год, подставив в уравнение t = ___:
Теперь рассчитайте среднее квадратическое отклонение фактических значений показателя убыточности от его теоретических значений:
Определите значение величины рисковой надбавки tσ при t=2 (σ = ______):
tσ = ___________________
Для того чтобы исчислить размер нетто-ставки на 9 год, суммируйте теоретическое значение уровня среднего показателя убыточности и рисковую надбавку, измеренную с вероятностью 0,954:
Нетто - ставка (на 9 год) = 
_______________________
Этот показатель ___________ показателя, рассчитанного на основе простой средней, поскольку на его значении отразилась тенденция увеличения убыточности, сложившаяся в 1– 8 годах.
2. По виду страхования №2 показатель убыточности развивается по ________________________функции, поэтому расчеты имеют следующий вид:
| Годы | Пубыт на 100 руб. страховой суммы | lgt | (lgt)2 | ylgt |
|
|
| 1. | 20,0 | |||||
| 2. | 23,0 | |||||
| 3. | 28,0 | |||||
| 4. | 31,0 | |||||
| 5. | 28,0 | |||||
| 6. | 30,0 | |||||
| 7. | 32,0 | |||||
| 8. | 32,0 | |||||
|
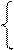
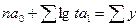
Изобразите полученные результаты на графике. Используя полученные данные, спрогнозируйте значение показателя убыточности на 9 год. Подставив в уравнение t = __, получим:
Тенденцию изменения показателя убыточности покажите на графике.
| Показатель убыточности, на 100 руб. страховой суммы | ||||||||||
Теперь рассчитайте среднее квадратическое отклонение фактических значений показателя убыточности от его теоретических значений:
На основе значений а получим величину рисковой надбавки tσ при при t=2 (σ = _______):
tσ = ______________________
Для того чтобы определить размер нетто-ставки, суммируйте теоретическое значение уровня среднего показателя убыточности на 9 год и рисковую надбавку, рассчитанную с вероятностью 0,954.
Нетто-ставка на 9 год будет равна _____________________руб. на 100 руб. страховой суммы.
3. Значение среднего показателя убыточности может иметь и другую тенденцию развития. Для расчета нетто-ставки на перспективу в этом случае прибегают к соответствующим приемам выравнивания.
Для вида страхования №3 сделайте следующие расчеты:
| Годы | Пу руб. | t | Пyt | Пyt2 | t2 | t3 | t4 |
| 
|
| 1. | 28,0 | ||||||||
| 2. | 31,0 | ||||||||
| 3. | 31,5 | ||||||||
| 4. | 37,0 | ||||||||
| 5. | 39,0 | ||||||||
| 6. | 43,0 | ||||||||
| 7. | 48,0 | ||||||||
| 8. | 55,5 | ||||||||
| 9. | 61,5 | ||||||||
| 10. | 77,0 | ||||||||
|
|
Решите систему уравнений.
Тенденцию изменения показателя убыточности покажите на графике.
| Годы | ||||||||||||||||||
Используя полученное уравнение, осуществите прогноз значения показателя убыточности на 11 год, подставив в уравнение t = ____.
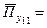
Теперь рассчитайте среднее квадратическое отклонение фактических значений показателя убыточности от его теоретических значений:
На основе значений а получим значение величины рисковой надбавки tσ при при t=3 (σ = _________): tσ = ______________________
Для того чтобы определить размер нетто-ставки, суммируйте спрогнозированное значение уровня среднего показателя убыточности на 11 год и рисковую надбавку, соответствующую вероятности 0,997. Нетто-ставка на 11 год: _____________________руб. на 100 руб. страховой суммы.
Тема 5. Индексы
Задача.
Исчисление индексов цен
| Товар | Единица измерения | Базисный период | Текущий период | Индиви-дуальные индексы цен ip = p1/ p0 | ||
| цена за единицу, тыс. руб. p0 | Количество q0 | цена за единицу, тыс. руб. p1 | Количество q1 | |||
| А | шт. | |||||
| Б | м | |||||
| В | т |
Исчислите агрегатный индекс цен по формуле, предложенной Г. Пааше:
По ассортименту товаров отчетного периода в целом цены повысились в среднем на _____%.
Абсолютный прирост товарооборота за счет роста цен в текущем периоде по сравнению с базисным периодом определим из индекса путем разности числителя и знаменателя, а именно:
Исчислите общий индекс цен по формуле Этьена Ласпейреса:
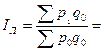
По ассортименту базисного периода в целом цены повысились в среднем на _____%.
Абсолютный прирост товарооборота, обусловленный повышением цен в текущем периоде по сравнению с базисным составил:
Таким образом, исчисление абсолютных и относительных показателей по разным формулам логично приводит к различным результатам. Индекс Пааше характеризует влияние изменения цен на стоимость товаров, реализованных в отчетном периоде, индекс Ласпейреса показывает влияние изменения цен на стоимость товаров, реализованных в базисном периоде. Это обусловливает применение индекса при прогнозировании товарооборота и цен на предстоящий период.
Тема 6. Выборочный метод
Выборочное статистическое исследование - это обследование выборочной совокупности с целью получения достоверных суждений о характеристиках или параметрах генеральной совокупности.
Генеральная совокупность - это полная совокупность единиц (статистическая совокупность).
Выборочная совокупность (выборка) – это часть единиц генеральной совокупности, отобранная в соответствии с принципами выборочного метода. Основное требование к отбору – он должен быть по возможности простым, отбор единиц в выборочную совокупность может быть повторным или бесповторным. При повторном – каждая отобранная единица возвращается в генеральную совокупность и может вновь попасть в выборку, при беcповторном – нет.
Сущность метода заключается в том, чтобы, не прибегая к обследованию всей генеральной совокупности, а, пользуясь данными только выборочной совокупности, определить обобщающие характеристики, полученные на основе данных выборочной совокупности. Выборочные характеристики всегда на какую-либо величину отличаются от генеральных. Величину отклонения иначе называют ошибкой выборочного наблюдения. При этом следует различать виды и способы отбора, при которых меняются методы расчета средней и предельной ошибок выборочного наблюдения, при определении среднего признака и доли (части совокупности, обладающей каким-то определенным признаком).
В статистике применяются различные способы формирования выборочных совокупностей, что обусловливается задачами исследования и зависит от специфики объекта изучения.
Существуют следующие способы отбора единиц из генеральной совокупности:
1) индивидуальный отбор – в выборку отбираются отдельные единицы;
2) групповой отбор – в выборку попадают качественно однородные группы или серии изучаемых единиц;
3) комбинированный отбор – это комбинация индивидуального и группового отбора.
Способы отбора определяются правилами формирования выборочной совокупности.
Собственно-случайная выборка состоит в том, что выборочная совокупность образуется в результате случайного (непреднамеренного) отбора отдельных единиц из генеральной совокупности. При этом количество отобранных в выборочную совокупность единиц обычно определяется исходя из принятой доли выборки.
Доля выборки есть отношение числа единиц выборочной совокупности n к численности единиц генеральной совокупности N, т.е. 
.
Так, при 5%-ной выборке из партии товара в 2 000 ед. численность выборки n составляет 100 ед. (5*2000:100), а при 20%-ной выборке она составит 400 ед. (20*2000:100) и т.д.
Механическая выборка состоит в том, что отбор единиц в выборочную совокупность производится из генеральной совокупности, разбитой на равные интервалы (группы). При этом размер интервала в генеральной совокупности равен обратной величине доли выборки.
Так, при 2%-ной выборке отбирается каждая 50-я единица (1:0,02), при 5%-ной выборке – каждая 20-я единица (1:0,05) и т.д.
На практике часто используют тот порядок, в котором фактически размещаются единицы генеральной совокупности. Например, последовательность выхода готовых изделий с конвейера или поточной линии, порядок размещения единиц партии товара при хранении, транспортировке, реализации и т.д.
Типическая выборка. При типической выборке генеральная совокупность вначале расчленяется на однородные типические группы. Затем из каждой типической группы собственно-случайной или механической выборкой производится индивидуальный отбор единиц в выборочную совокупность. Например, при выборочном обследовании производительности труда работников торговли, состоящих из отдельных групп по квалификации.
При одноступенчатой выборке каждая отобранная единица сразу же подвергается изучению по заданному признаку. Так обстоит дело при собственно-случайной и серийной выборке.
При многоступенчатой выборке производят подбор из генеральной совокупности отдельных групп, а из групп выбираются отдельные единицы. Так производится типическая выборка с механическим способом отбора единиц в выборочную совокупность.
Комбинированная выборка может быть двухступенчатой. При этом генеральная совокупность сначала разбивается на группы. Затем производят отбор групп, а внутри последних осуществляется отбор отдельных единиц.
Задача. В населенном пункте проживает 250 тыс. семей. Для определения среднего числа детей в семье была организована 2% случайная бесповторная выборка семей. По ее результатам было получено следующее распределение семей по числу детей:
| Число детей в семье | ||||||
| Количество семей |
С вероятностью 0,954 найдите пределы, в которых будет находиться среднее число детей в генеральной совокупности.
Решение: Вначале определим выборочную среднюю и дисперсию.
Расчет для определения средней и дисперсии выборки
| Число детей в семье xi | Количество семей fi | xi· fi | xi-x | (xi-x)2 | (xi-x)2· fi |
| Итого |
x = xi· fi / Σ fi =
σ2x = (xi-x)2· fi / Σ fi
Исчислим предельную ошибку выборки с учетом P = 0.954, t = 2.
Δx = 
Следовательно, пределы генеральной средней X = X + Δx
Вывод: с вероятностью 0,954 можно утверждать, что среднее число детей в семье практически не отличается от ___, т.е. в среднем на каждые две семьи приходится ___ ребенка.
