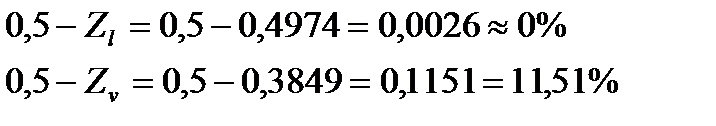Выполнил студент 4-ИТ-5____________________Е.В. Синева
подпись, дата
Проверил к.т.н., доцент _____________________Н.А. Сазонникова
подпись, дата
Самара 2007
Полученные данные это результаты измерения размеров 100 деталей (в мм). Необходимо:
1 Построить контрольный листок;
2 Провести предварительную обработку данных:
2.1 определить выборочное среднее – оценку математического ожидания;
2.2 определить исправленную выборочную дисперсию;
2.3 проверить закон распределения на нормальность;
2.4 построить гистограмму;
3 Вычислить индекс воспроизводимости процесса Ср и Срк, определить процент брака;
4 Построить диаграмму Парето, проведя расслоение по:
4.1 станкам 1–50 – 1 станок
51–100 – 2 станок;
4.2 времени сбора информации
1 мес. 1 – 25
51 – 75
2 мес. 26 – 50
76 – 100;
4.3 контрольно-измерительным приборам
1 прибор 1 – 13, 51 – 63
2 прибор 14 – 25, 64 – 75
3 прибор 26 – 38, 76 – 88
4 прибор 39 – 50, 89 – 100
5 Построить диаграмму Исикавы
Содержание
1 Предварительная обработка данных.. 4
1.1 Нахождение размаха. 4
1.2 Определение выборочного среднего – оценки математического ожидания. 5
1.3 Определение исправленной выборочной дисперсии. 5
1.4 Проверка закона распределения на нормальность. 5
1.5 Построение контрольного листка. 8
2 Расчет коэффициента годности изделий Ср и показателя мощности процесса Срк. 11
4 Построение диаграммы Исикавы.. 13
5 Построение диаграмм Парето.. 14
6 Построение Х-R контрольной карты.. 16
1 Предварительная обработка данных
Таблица 1 результаты 100 измерений
| 41.32 | 41.33 | 41.28 | 41.26 | 41.25 | 41.29 | 41.30 | 41.28 | 41.32 | 41.29 |
| 41.31 | 41.25 | 41.24 | 41.23 | 41.22 | 41.29 | 41.31 | 41.28 | 41.27 | 41.27 |
| 41.28 | 41.23 | 41.27 | 41.24 | 41,22 | 41.25 | 41.27 | 41.30 | 41.24 | 41.30 |
| 41.32 | 41.24 | 41.26 | 41.26 | 41.25 | 41.26 | 41.31 | 41.27 | 41.26 | 41.30 |
| 41.23 | 41.29 | 41.26 | 41.28 | 41.25 | 41.25 | 41.30 | 41.27 | 41.31 | 41.26 |
| 41.26 | 41.29 | 41.26 | 41.28 | 41.26 | 41.29 | 41.29 | 41.27 | 41.30 | 41.27 |
| 41.27 | 41.21 | 41.26 | 41.28 | 41.23 | 41.27 | 41.30 | 41.30 | 41.27 | 41.25 |
| 41.27 | 41.25 | 41.28 | 41.26 | 41.27 | 41.27 | 41.28 | 41.30 | 41.27 | 41.26 |
| 41.30 | 41.25 | 41.27 | 41.26 | 41.28 | 41.27 | 41.28 | 41.30 | 41.29 | 41.27 |
| 41.31 | 41.25 | 41.26 | 41.27 | 41.29 | 41.32 | 41.29 | 41.30 | 41.27 | 41.32 |
Для удобства обработки значений отбросим целую часть.
1.1 Нахождение размаха

Так как размах равен 12, то целесообразно разбить данные на 6 интервалов с шагом, равным 2.
| № интервала | Границы интервала | Середина интервала | Частота попадания в интервал, Пi | ∑Пi | Пi/n, n=100 | Накопленная относительная частота, ∑Пi/n |
| 21-23 | 0,07 | 0,07 | ||||
| 23-25 | 7+14=21 | 0,14 | 0,21 | |||
| 25-27 | 21+35=56 | 0,35 | 0,56 | |||
| 27-29 | 56+21=77 | 0,21 | 0,77 | |||
| 29-31 | 77+17=94 | 0,17 | 0,94 | |||
| 31-33 | 94+6=100 | 0,06 |
1.2 Определение выборочного среднего – оценки математического ожидания
Несмещенной, состоятельной и эффективной оценкой математического ожидания является среднеарифметическое, вычисленное по результатам n независимых наблюдений над случайной величиной Х:

1.3 Определение исправленной выборочной дисперсии
Состоятельной, несмещенной и эффективной оценкой дисперсии является величина:
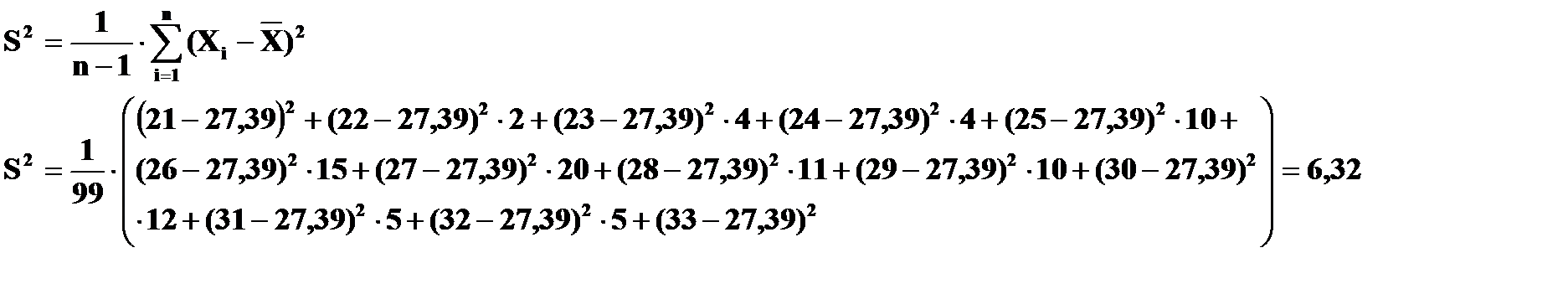
1.4 Проверка закона распределения на нормальность
Проверка гипотезы о виде распределения осуществляется по критерию Пирсона χ2

f – наблюдаемые частоты;
f’ – теоретические частоты, которые соответствуют выбранному закону 
Таблица 3 Результаты расчета F’
| Границы интервала | Частота попадания в интервал | Середина интервала | 
| Z | Ф(Z) | F’ |
| 21-23 | -5,4 | -2,15 | 0,0396 | 3,156 | ||
| 23-25 | -3,4 | -1,35 | 0,1604 | 12,78 | ||
| 25-27 | -1,4 | -0,56 | 0,3410 | 27,18 | ||
| 27-29 | 0,6 | 0,24 | 0,3876 | 30,89 | ||
| 29-31 | 2,6 | 1,04 | 0,2323 | 18,51 | ||
| 31-33 | 4,6 | 1,83 | 0,0748 | 5,96 |

После нахождения значений Z по таблице значений функции нормального распределения находим Ф(Z).
Далее находим Fʹ

Fʹ= 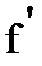 *Ф(Z)
*Ф(Z)
Далее находим

1.5 Построение контрольного листка
Контрольный листок является вспомогательным методом для построения гистограмм, диаграмм Парето, контрольных карт. Контрольный листок – инструмент для сбора первичной информации, ее фиксации и автоматического упорядочения. Контрольный листок обеспечивает наглядность и полноту данных.
| Номинальное значение 27 мм | ||||||||||||||||||||||
| х | ||||||||||||||||||||||
| х | х | |||||||||||||||||||||
| х | х | х | х | |||||||||||||||||||
| х | х | х | х | |||||||||||||||||||
| х | х | х | х | х | х | х | х | х | х | |||||||||||||
| х | х | х | х | х | х | х | х | х | х | х | х | х | х | х | ||||||||
| х | х | х | х | х | х | х | х | х | х | х | х | х | х | х | х | х | х | х | х | |||
| х | х | х | х | х | х | х | х | х | х | х | ||||||||||||
| х | х | х | х | х | х | х | х | х | х | |||||||||||||
| х | х | х | х | х | х | х | х | х | х | х | ||||||||||||
| х | х | х | х | х | ||||||||||||||||||
| х | х | х | х | х | ||||||||||||||||||
| х |
Рисунок 1 – контрольный листок
Из данного контрольного листка видно, что из ста полученных результатов измерения наиболее часто встречается значение 41,27 20 раз, 41,26 15 раз, а закон распределения близок или является нормальным.
1.6 Построение гистограммы
Гистограмма – это инструмент представления данных, сгруппированных по частоте попадания в некоторый интервал, это столбиковая диаграмма, служащая для графического представления имеющейся информации. При простоте построения гистограмма дает много полезной информации о разбросе качественных показателей, о средних значениях, о точностных возможностях технического оборудования.
Порядок построения гистограммы:
1 Определение наибольшего (λ) и наименьшего (S) значений среди данных.
λ=33
S=21
Интервал между λ и S делится на участки.
2 Определение ширины участка h.
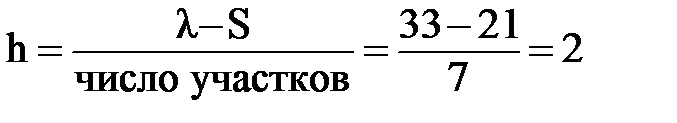
3 Определение значения границ участков
Сначала находят наименьшее граничное значение для первого участка, как

Прибавляя к полученному значению величину h, получают границы остальных участков:
20,5+2=22,5
22,5=2=24,5
24,5+2=26,5
26,5+2=28,5
28,5+2=30,5
30,5+2=32,5
32,5+2=34,5
4 Определение частоты попадания в каждый интервал
Таблица 4 Частоты попадания в интервал
| Границы интервала | Частота попадания |
| 20,5–22,5 | |
| 22,5–24,5 | |
| 24,5–26,5 | |
| 26,5–28,5 | |
| 28,5–30,5 | |
| 30,5–32,5 | |
| 32,5–34,5 |
5 Построение графика гистограммы

Рисунок 2 - Гистограмма распределения
2 Расчет коэффициента годности изделий Ср и показателя мощности процесса Срк
Т=100 мкм=0,1мм, номинальный размер равен 41,25.
2.1 Рассчитаем верхнюю и нижнюю границу поля допуска:
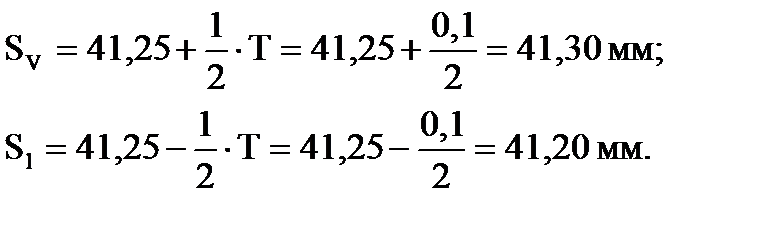

Рисунок 3 – Гистограмма распределения с нанесенными границами поля допуска
2.2 Рассчитаем коэффициент годности изделий и показатель мощности процесса Ср и Срк
Для количественное оценки того, сколько изделий вошло в поле допуска используется коэффициент годности (Ср). Исследование воспроизводимости процесса с помощью этого коэффициента позволяет оценить качество процесса в соответствии с требованиями потребителя. Чем больше Ср, тем выше качество процесса, тем меньше вероятность его несоответствия ожиданиям потребителя.

Из этого следует, что процесс неконтролируем, ширина интервала не превышает величины 4S, процент брака превышает 4,56%. Необходим сплошной контроль продукции, чтобы предотвратить выпуск бракованной продукции.

2.3 Далее рассчитаем процент бракованных изделий
Для этого определим нормированные отклонения верхней и нижней границы от  :
:

Затем, пользуясь таблицей функции нормального распределения определим вероятность попадания в интервалы (0;Zv) и (Zl;0). Получим следующие значения:

Процент брака по верхней и по нижней границам: