Абсолютні показники варіації

Методичні вказівки та завдання

до виконання розрахункової роботи

з дисципліни ''Статистика''

студентами за напрямом підготовки

«Менеджмент організацій»

 

 

Рівне 2012

 

 

Упорядник: Н.С. Качан, старший викладач кафедри трудових ресурсів і підприємництва.

 

 

Зміст

Вступ …………………………………………………………………
1. Вимоги до змісту та оформлення розрахункової роботи ………...
2. Завдання і методичні рекомендації до виконання розрахункової роботи ………………………………………………………………..
	Завдання 1……………………………………………………….
	Завдання 2……………………………………………………….
	Завдання 3……………………………………………………….
	Завдання 4……………………………………………………….
Додатки……………………………………………………………....

© Н.С. Качан, 2012

© НУВГП, 2012

Вступ

Статистика є однією із фундаментальних економічних наук, а статистичний інструментарій та методи широко використовуються у практичній діяльності. У сучасних умовах оволодіння методологією статистики є однією з неодмінних умов пізнання закономірностей розвитку соціально-економічних процесів, дослідження особливостей ринкової кон'юнктури, вивчення тенденцій та прогнозування розвитку економічних явищ. Інформація, отримана в ході статистичних досліджень та аналізу сприяє прийняттю оптимальних управлінських рішень на всіх рівнях господарювання. Як дисципліна статистика забезпечує формування у фахівців економічної підготовки комплексу професійних знань щодо організації досліджень, збору, оброблення та аналізу одержаних даних.

Метою розрахункової роботи є набуття студентами навичок практичного використання теоретичних знань зі статистики, зокрема:

- зі зведення і групування даних статистичного спостереження;

- із визначення середніх величин, моди і медіани, встановлення їх типовості як характеристик сукупності;

- із виявлення та аналізу взаємозв'язків між ознаками різними способами, оцінювання та аналізу щільності зв'язку у випадку парної лінійної залежності, визначення параметрів лінійного рівняння регресії та побудови емпіричної та теоретичної лінії регресії;

- з аналізу рядів динаміки;

- із визначення індивідуальних і зведених індексів та застосування їх у факторному аналізі соціально-економічних явищ і процесів.

Методичні вказівки містять такі структурні частини: вступ, вимоги до змісту та оформлення, завдання і методичні рекомендації до виконання розрахункової роботи, додатки, які складаються з вихідних даних та довідкової інформації.

Завдання розрахункової роботи охоплюють переважну більшість тем, які повинні засвоїти студенти заочної форми навчання згідно з робочою програмою дисципліни.

Вимоги до змісту та оформлення

Розрахункової роботи

У пункті 2 методичних вказівок подано умови 4 завдань, що складаються із задач, які необхідно розв’язати відповідно до індивідуального варіанту та методичних рекомендацій до їх виконання. Вихідні дані до розрахункової роботи та допоміжна довідкова інформація наведено у додатках.

Номер індивідуального варіанту завдання – це номер студента у списку академічної групи.

Контрольна робота повинна містити: умови задач, відповідно оформлені таблиці і графіки; формули, до них розрахунки і пояснення. Важливою частиною виконання роботи є висновки у вигляді економічної інтерпретації отриманих результатів.

Контрольна робота виконується в зошиті (12 – 18 аркушів) або на стандартних листах не більше 10 – 12 аркушів формату А4 (210´297 мм), шрифтом 12 кегль, одинарний інтервал на одній стороні аркуша.

На титульному листі вказується назва вищого навчального закладу, факультету, кафедри, дисципліни, відомості про студента: прізвище, ім’я, по-батькові, спеціальність, курс, група, варіант, номер залікової книжки. Сторінки розрахункової роботи нумеруються.

Завдання і Методичні рекомендації до

Виконання розрахункової роботи

 

Завдання 1

Задача 1

Використовуючи дані управлінського обліку 20 рекламних агентств у регіоні щодо зміни витрат на навчання і підвищення кваліфікації одного працівника у поточному році в порівняні з попереднім - факторна ознака, (додаток А, таблиця А 1), побудувати ряд розподілу, утворивши групи з рівними закритими інтервалами. Результати групувань викласти у формі статистичної таблиці.

Задача 2

Знайти середню величину зміни (абсолютного приросту) витрат на навчання і підвищення кваліфікації одного працівника у поточному році в порівняні з попереднім, моду, медіану. Пояснити зміст отриманих значень показників. Зробити висновок про форму розподілу рекламних агентств за абсолютним приростом витрат на навчання і підвищення кваліфікації одного працівника.

Задача 3

Визначити абсолютні і відносні показники варіації. Пояснити зміст отриманих значень показників. Зробити висновки про ступінь однорідності сукупності. Визначити коефіцієнт асиметрії. Зробити висновок про форму асиметрії розподілу рекламних агентств за факторною ознакою та ступінь асиметричності розподілу.

Методичні рекомендації до виконання завдання 1

Задача 1

Результати розрахунків викласти в у табличній формі:

Таблиця 1

Розподіл рекламних агентств за абсолютним приростом

витрат на навчання і підвищення кваліфікації одного працівника

Групи за абсолютним приростом витрат, грн.	Частота в групі, f
...	...
Разом

 

У розрахунках використати формули:

Величина інтервалу (h):

, (1.1)

де x_max, x_min – відповідно найбільше і найменше значення ознаки в сукупності;

m – кількість груп.

Кількість груп (m):

, (1.2)

де n – кількість елементів сукупності.

Задача 2

Результати розрахунків викласти у табличній формі:

Таблиця 2

Вихідні дані для розрахунку моди і медіани

Групи за абсолютним приростом витрат, грн.	Середина інтервалу, грн., xі	Частота в групі, f	Накопичена частота, од., Sf
...	...	...
Разом		-

 

У розрахунках використати формули:

Середня арифметична зважена (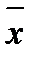 - величина, яка характеризує типовий рівень ознаки в сукупності):

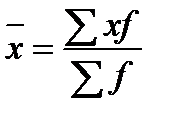, (1.3)

де x – окремі значення ознаки в сукупності (тут: середина інтервалу x_і);

f – частота появи ознаки в сукупності.

Середина інтервалу (x_і):

, (1.4)

де x_*, x^* - відповідно найбільше і найменше значення ознаки в інтервалі.

Мода (М_о – варіанта, яка в ряді розподілу має найбільшу частоту, тобто частку):

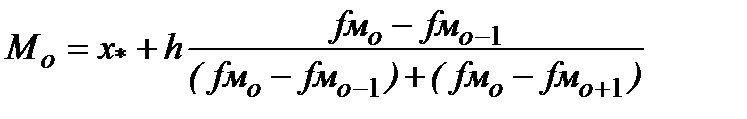, (1.5)

де x_* – найменше значення ознаки в модальному інтервалі;

h – ширина модального інтервалу;

f_мо – частота модального інтервалу;

f_мо-1 – частота передмодального інтервалу;

f_мо+1 – частота післямодального інтервалу.

Медіана (М_е – варіанта, яка ділить упорядкований ряд розподілу на дві рівні частини):

, (1.6)

де x_* – найменше значення ознаки в медіанному інтервалі;

h – ширина медіанного інтервалу;

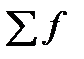- сума частот;

Sf_ме-1 – накопичена частота передмедіанного інтервалу;

f_ме – частота медіанного інтервалу.

Форми розподілу:

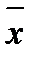= М_е = М_о – розподіл симетричний;

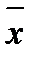> М_е > М_о – правостороння асиметрія;

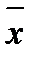< М_е < М_о – лівостороння асиметрія.

Задача 3

Результати розрахунків викласти у табличній формі:

Таблиця 3

Вихідні дані для визначення абсолютних і відносних

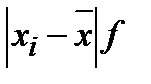
Групи за абсолютним приростом витрат, грн.	Середина інтервалу, грн. xі	Частота в групі f			()2	()2 f
...	...	...
Разом

показників варіації

 

У розрахунках використати формули:

Абсолютні показники варіації

Розмах варіації (R):

R = x_max - x_min. (1.7)

Середнє лінійне відхилення зважене ():

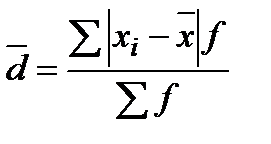. (1.8)

Середнє квадратичне відхилення зважене (σ):

. (1.9)

Дисперсія зважена (σ² – середній квадрат відхилення):

. (1.10)

Якщо σ = 1,25 або R = 6·σ = 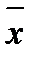± 3σ, то розподіл є симетричним, близьким до нормального.