Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
Закон распределения дискретной случайной величины обычно задается рядом распределения, который представляется в виде таблицы:

| 
| 
| … | 
|

| 
| 
| … | 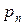
|
где в первой строке перечислены все возможные значения случайной величины, а во второй – соответствующие им вероятности 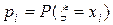 , удовлетворяющие соотношению
, удовлетворяющие соотношению  .
.
Закон распределения может быть задан графически в виде многоугольника распределения вероятностей, т.е. в виде ломаной, соединяющей точки с координатами  для
для 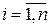 .
.
Математическим ожиданием или средним значением дискретнойслучайной величины  называется сумма произведений всех ее возможных значений на соответствующие им вероятности:
называется сумма произведений всех ее возможных значений на соответствующие им вероятности:
 . (7)
. (7)
Дисперсией случайной величины  называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания, т.е.
называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания, т.е.
 . (8)
. (8)
Для вычисления дисперсии на практике бывает удобнее использовать другую формулу, которую можно получить из формулы (8) с помощью простых преобразований:
 . (9)
. (9)
Средним квадратическим отклонением или стандартным отклонением случайной величины называется корень квадратный из ее дисперсии:
 . (10)
. (10)
Непрерывная случайная величина и ее числовые характеристики
Закон распределения непрерывной случайной величины  удобно задавать с помощью функции плотности вероятности
удобно задавать с помощью функции плотности вероятности  . Вероятность
. Вероятность 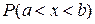 того, что значение, принятое случайной величиной
того, что значение, принятое случайной величиной  , попадет в интервал
, попадет в интервал  , определяется равенством:
, определяется равенством:
 .
.
Математическим ожиданием или средним значением непрерывной случайной величины  с плотностью распределения вероятности
с плотностью распределения вероятности  называется число:
называется число:
 ,
,
если этот интеграл сходится абсолютно. В противном случае математическое ожидание случайной величины  не существует.
не существует.
Дисперсия непрерывной случайной величины определяется также, как и для дискретной. Для непосредственного вычисления дисперсии используют формулы:
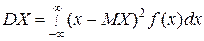 или
или  .
.
Нормальное распределение
Непрерывная случайная величина имеет нормальное или гауссовское распределение с параметрами  и
и 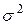 , где
, где  и
и  (пишут
(пишут  ), если функция плотности случайной величины имеет вид:
), если функция плотности случайной величины имеет вид:
 ,
,
для любого  .
.
При 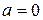 и
и  , т.е.
, т.е.  , нормальный закон распределения называется стандартным или нормированным.
, нормальный закон распределения называется стандартным или нормированным.
Если случайная величина  имеет нормальное распределение с параметрами
имеет нормальное распределение с параметрами  и
и 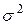 , то
, то
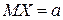 и
и  .
.
Найти вероятность попадания случайной величины  , распределенной по нормальному закону с параметрами
, распределенной по нормальному закону с параметрами  и
и 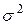 , в интервал
, в интервал 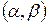 можно по формуле:
можно по формуле:
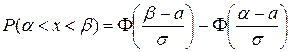 , (11)
, (11)
где  – функции Лапласа, значения которой определяются по таблице. При использовании таблицы необходимо учитывать, что функция
– функции Лапласа, значения которой определяются по таблице. При использовании таблицы необходимо учитывать, что функция  является нечетной и при
является нечетной и при 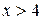 значения
значения  считаются равными 0,5.
считаются равными 0,5.
Математическая статистика






