Выпуск товарной продукции и ее оптовая цена

60,2

2003

32,6

9

10)

11. 14 15" 16 17_ J3_ 19.20 21 22 23 24 25 26 27 28 29 30_ зД

12_

186,6

 

Заболеваемость населения наркоманией (на 100 000 человек населения)

 

	144.4/*^
	62,6^*
	60,2 Jr
	44 ^^^ic^
19,1

1999 2000 2001 2002 2003 2004 2005 2006

 

Рис. 4.10. Вид рабочего листа после построения диаграммы

 

быть отражена как во время создания диаграммы, так и позднее. Если легенда создается одновременно с диаграммой, в Мастере диаграмм на третьем шаге на вкладке Легенда ставится флажок напротив соответствующей опции. Если легенда добавляется позднее, в свободном поле диаграммы выполняется щелчок пра­вой клавишей мыши и из контекстного меню выбирается ко­манда Параметры диаграммы. В результате открывается то же самое диалоговое окно.

Результат работы будет выглядеть следующим образом (рис. 4.12).

Ввод e действие жилых домов (на
________ 1000 человек населения) ____________________

Общая площадь, кв. м

¹

3 4

_L

_7_ 8

14 1A 16 17 18 19 20 21. 22 23 24"

9_ J£ 11 11 1_3 год

 

1997 1998

 

в городах и поселках городского типа

285 298

230 220 228 218 231

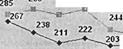Ввод в действие жилых домов (на 1000 человек населения)

 

Год

1997 1998 1999 2000 2001 2002 2003 2004 2005 2006 2007

- Общая площадь, кв. м в сельской местности

- Общая площадь, кв. м в городах и поселках городского типа

 

Рис. 4.12. Вид рабочего листа книги Excel

 

вают диалоговое окно Выбор рисунка, в котором указывают файл с интересующим изображением. Результат показан на рис. 4.13. Более подробно приемы работы изложены в приложении 6.

Для наглядного сравнения объемов изучаемых явлений во времени или в пространстве, а также для изображения структуры явлений используются столбиковые диаграммы. Столбиковыми диаграммами называют графические изображения статистичес­ких данных в виде вертикально размещенных столбиков — пря­моугольников, у которых все основания равны, а их высота про­порциональна числовым значениям изображаемых показателей, т. е. для всех столбиков принимается один и тот же масштаб. Все столбики строятся на одной базовой линии. О соотношении между величинами изображаемых показателей судят по высоте столби­ков, поэтому разрыв шкалы для них не допускается.

Рис. 4.13. Вид рабочего листа после создания вспомогательной оси

 

На рис. 4.14 изображена столбиковая диаграмма, показыва­ющая структуру валового внутреннего продукта по видам пер­вичных доходов (в текущих ценах).

Для построения гистограммы, представленной на рис. 4.14, в Excel также используется Мастер диаграмм. В качестве типа диаграммы выбран объемный вариант гистограммы с накоплени­ем. Исходные данные и результат их обработки представлены на рис. 4.15.

Для изображения структуры совокупности, как правило, ис­пользуются секторные диаграммы. Они представляют собой гра­фическое изображение результатов статистического наблюдения в виде площадей, образуемых секторами круга. При этом на по­верхности круга той или иной части наблюдаемого статисти­ческого явления отводится сектор с числом градусов по окруж­ности, пропорциональным удельному весу этой части явле­ния во всем его объеме, принимаемом за 100% (так как окруж­ность имеет 360 градусов, то каждому проценту соответствует 3,6 градуса).

2003 2004 2005 2006 Год

□ Валовая прибыль экономики и валовые смешанные доходы

□ Чистые налога на производство и импорт

□ Скрытая оплата труда

□ Официальная оплата труда

Рис. 4.14. Столбиковая диаграмма. Структура валового внутреннего продукта

 

_| А _ J___ __________ В_____ [_____ С___ ]_________ D____ Е I F < 9

, Структура валового внутреннего продукта

 

		Валовая прибыль	Чистые налоги на	Скрытая	Официальная
	Год	экономики п валовые	производство и	оплата	оплата
		мешанные д	1 ы т	труда.*.	труда.%

Струтчуро валового внутреннего продукта

Офнцмальн оплат труда,'; _Sl

25 | кр пая оплата треда.

26 ' ■ -г
2j О Чистые налоги на производство и i. *•

28 I а Валовая при ы ль экономики н валовые с шины доходы,*

29 I_____:_________ *

Рис. 4.15. Вид рабочего листа Excel после построения гистограммы

На рис. 4.16 изображена секторная диаграмма, характеризу­ющая состав численности работников органов государственной власти и местного самоуправления. Отдельные секторы для на­глядности отличаются разной расцветкой или штриховкой.

Законодательная власть

Исполнительная власть и местное самоуправление Судебная власть и прокуратура Другие государственные органы

 

 

Рис. 4.16. Секторная диаграмма. Численность работников органов государственной власти и местного самоуправления по ветвям власти

 

Вид секторной диаграммы в Excel представлен на рис. 4.17 (см. также приложение 6).

Если значение одного из секторов должно быть детализиро­вано, в Excel используют круговую диаграмму с частью значений, вынесенных в гистограмму. На рис. 4.18 представлен образец ис­пользования подобного типа диаграммы. Деление государствен­ных органов на виды а, в, с условное.

В некоторых случаях применяют фигурные диаграммы, кото­рые чаще всего используют для популяризации статистической

7-2447

.B__L

 

 

5_ J5_ _7_ 8 9" 10 11 J2 13

Л J5

I⁶ J7_

J8

J9

Ж 21

22 23

2£ 25 26 27

Численность работников органов государственной власти и местного самоуправления по ветвям власти

Законодательная власть _ 9,9%

Исполнительная власть 88,5%

Судебная власть и прокуратура 1.3%

88,5

нЗаконодательная власть □ Судебная власть и прокуратура

Другие государственные органы. 0,3%

□Исполнительная власть

□Другие государственные органы.

 

Рис. 4.17. Вид рабочего листа Excel после построения секторной диаграммы

 

информации. Они представляют собой изображения в форме рисунков, соответствующих материальному содержанию иссле­дуемых явлений, на которых величина изображаемого показате­ля пропорциональна площади фигуры, изображающей данное явление. Например, представление о производстве автомашин (или другой продукции) в разных странах или в одной стране за ряд лет можно дать с помощью изображения автомашин разно­го размера, площадь которых пропорциональна изображаемым

Численность работников органов государственной власти и местного самоуправления по ветвям власти

 

 

_9_ 10

11 11 "13

J 4

X⁵ 16 J7 J 8

J.9 20"

22 23 24 25

__2_6_ 27 28 29

Ж 31

"33 _< "34

 

Законодательная власть__ Исполнительная власть Судебная власть и прокуратуру Другие государственные органы, в том числе: а в

88,5

Численность работников органов государственной сласти и местного самоуправления по ветвям власти. %

 

ниш	^-0,05
МИШ	---- 0.10
> Л W	0,15

□ Законодательная власть

□ Исполнительная власть

□ Судебная власть и прокуратура

■ Другие государственные органы, в том числе: па

08 0 С

i

 

Рис. 4.18. Вид рабочего листа Excel после построения секторной диаграммы с частью значений, вынесенных в гистограмму

 

числовым показателям. Динамику добычи угля можно изобра­зить, нарисовав вагоны, число которых пропорционально чис­лам ряда динамики.

Возможности такого изображения статистических рядов весь­ма разнообразны.

2001 2002 2003 2004 2005 2006

 

Рис. 4.19. Фигурная диаграмма грузоперевозки морского торгового флота

 

В Excel построение графиков подобного типа может осуще­ствляться на основе любого графика, фоном для которого слу­жит рисунок или фотография заданной тематики.

В статистике используется еще особый вид графических изоб­ражений экономических показателей — картограммы и карто­диаграммы. Этот вид графиков предусматривает нанесение того или иного изображения экономических показателей на геогра­фические карты.

Картограммы — это изображение величины интересующего нас признака на географической карте с помощью графических символов: штриховки, расцветки, точек.

Для построения картограммы надо изображаемый на карте показатель разделить на интервалы или группы по интенсивно­сти проявления наблюдаемого явления и определить для каждо­го из них густоту штриховки или окраски. При этом штриховать или красить надо тем гуще, чем больше размер показателя. Та­ким образом, если обозначить разную плотность населения в административно-территориальных федеральных округах Рос­сийской Федерации и соответственно заштриховать эти районы на географической карте, то будет наглядно видно различие плот­ности распределения населения по стране. Для получения ко­личественных характеристик исследуемых величин и для анали­за корреляционных связей между ними на картограммах могут использоваться изолинии.

Изолинии (от греческого isos — равный, одинаковый, подоб­ный) — это линии равного значения какой-либо величины в ее распространении на поверхности, в частности на географичес­кой карте или графике. Изолиния отражает непрерывное изме­нение исследуемой величины в зависимости от двух других пе­ременных и применяется при картографировании природных и социально-экономических явлений.

Наглядным примером построения картограммы может слу­жить группировка субъектов Российской Федерации по числен­ности населения (рис. 4.20).

Если после заштриховки или окраски соответствующих уча­стков карты обнаруживается определенная закономерность в географическом расположении территории с одинаковой вели­чиной изображаемого показателя, то можно говорить о зависи­мости данного показателя от географического фактора. Если же районы с одинаковой окраской или штриховкой разбросаны в беспорядке на карте, то, очевидно, нет определенной законо­мерности в пространственном размещении данного показателя, т.е. его распространение или уровень не связаны с географичес­ким расположением района.

Картодиаграмма — это сочетание географической карты и диаграммы. На картодиаграммах распределение показателей по территории дается на схематической географической карте в форме столбиков, треугольников, силуэтов зданий, нефтяных вышек и других графических символов. Современные информационные технологии позволяют моделировать трехмерные картодиаграм­мы, в том числе имитирующие перемещение над выбранным уча­стком географической карты с одновременным динамично меня­ющимся отображением статистических показателей. Такие технологии требуют значительных вычислительных ресурсов, по­этому используются в проектах государственного масштаба (как правило, при организации выборов). С трехмерными картодиаг­раммами можно ознакомиться, к примеру, на сайте http:// www.mercator.ru/.

Источник. Официальный сайт Федеральной службы Государственной статистики Российской Федерации, 2007 г.

Рассмотренные виды графиков наиболее часто употребляемы. Графические изображения социально-экономических показателей придают письменному или устному изложению особую нагляд­ность. Графики служат не только средством наглядности для ил­люстрации количественных закономерностей, но играют также большую роль в сравнительной оценке и статистическом анализе различных видов эмпирических распределений. Графики являют­ся методом обобщения исследуемой информации. Они позволяют осуществить контроль достоверности статистических данных.

Тесты к главе 4

1. Абсолютная статистическая величина — это:

а) качественный показатель размера или объема исследуемо-
го явления, не зависящий от времени и территории;

б) количественный показатель размера или объема исследуе-
мого явления в конкретное время и на определенной территории;

в) качественный показатель размера или объема исследуемо-
го явления в конкретное время и на определенной территории.

2. Абсолютная статистическая величина измеряется:

а) в натуральных именованных числах;

б) в процентах;

в) в долях единицы.

3. Объем совокупности — это:

а) численность единиц, составляющих статистическую сово-
купность;

б) сумма всех значений усредняемого признака по совокуп-
ности;

в) произведение числа единиц в совокупности на сумму всех
значений усредняемого признака.

4. Относительная величина — это:

а) показатель, получаемый как частное отделения одной вели-
чины на другую, характеризующий количественные соотношения
между социально-экономическими явлениями или процессами;

б) показатель, получаемый как произведение одной величи-
ны на другую, характеризующий количественные соотношения
между социально-экономическими явлениями или процессами;

в) показатель, получаемый как разность от вычитания одной
величины из другой, характеризующий количественные соотно-
шения между социально-экономическими явлениями или про-
цессами.

5. Относительная статистическая величина измеряется:

а) в натуральных физических единицах;

б) в условно-натуральных;

в) в долях единицы или процентах.

6. Относительная величина, характеризующая изменение яв-
лений во времени, — это:

а) относительная величина динамики;

б) относительная величина сравнения;

в) относительная величина интенсивности.

7. Относительная величина, характеризующая сопоставление
величин однородных явлений, относящихся к различным объек-
там за один и тот же период времени, — это:

а) относительная величина динамики;

б) относительная величина сравнения;

в) относительная величина интенсивности.

8. Относительная величина, характеризующая степень разви-
тия исследуемого явления в определенной среде, — это:

а) относительная величина динамики;

б) относительная величина сравнения;

в) относительная величина интенсивности.

9. При построении линейной диаграммы используются шкалы:

а) равномерные;

б) неравномерные;

в) логарифмические.

10. Изображение величины признака на географической карте
с помощью графических символов — это:

а) фигурные диаграммы;

б) картограммы;

в) картодиаграммы.

11. Сочетание географической карты и диаграммы - это:

а) картодиаграмма;

б) картограмма;

в) фигурная диаграмма.

Глава 5

 

СРЕДНИЕ ВЕЛИЧИНЫ

И ПОКАЗАТЕЛИ ВАРИАЦИИ

 

 

5.1.

Средние величины, их сущность и значение

При обработке и анализе статистического материала, кроме сравнительных данных (в виде относительных величин), часто возникает необходимость получить обобщающую харак­теристику уровня изучаемых явлений. Как правило, цифровое значение того или иного признака у отдельных единиц совокуп­ности неодинаково. В этом случае требуется определить сред­нюю величину признака, которая давала бы обобщающую ха­рактеристику совокупности.

Например, если возникла необходимость сопоставить зара­ботную плату рабочих трех предприятий, входящих в одну и ту же отрасль, то, очевидно, что заработная плата отдельных рабо­чих не может быть использована для такого сравнения, так как она будет зависеть от уровня их квалификации, стажа работы и многих других причин. Значит, надо сравнивать не индивидуаль­ные, а обобщающие показатели уровня заработной платы. Одной из таких обобщающих характеристик может рассматриваться фонд заработной платы всех рабочих каждого завода, но этот показа­тель также непригоден для решения поставленной задачи, так как при прочих равных условиях общая сумма заработной платы тем больше, чем больше рабочих на данном предприятии. Следо­вательно, лишь разделив фонд заработной платы на число рабо­чих и получив среднюю заработную плату по каждому предприя­тию, можно сравнить полученные величины и определить, на каком предприятии уровень заработной платы рабочих выше.

Средней величиной в статистике называется обобщающий показатель, который характеризует типичный уровень варьиру­ющего признака в расчете на единицу совокупности в конкрет­ных условиях места и времени. Средняя величина всегда имеет ту же размерность, что и варьирующий признак.

Метод средних является одним из важнейших статистических методов, но он неотделим от метода группировок. Основным ус­ловием правильного научного использования средней величины в статистике является качественная однородность совокупности, по которой исчислена средняя. В связи с этим перед исчислени­ем средних величин все единицы совокупности расчленяют на однородные группы, по которым и исчисляют средние.

Метод средних неотделим от метода группировок, так как именно группировки обеспечивают качественную однородность исследуемых статистических совокупностей.

Но и одних только средних показателей недостаточно для оценки тех или иных явлений. Средние уравнивают, сглаживают индивидуальные особенности отдельных единиц совокупности и тем самым могут затушевывать проявление различных тенден­ций. Средние величины широко используются при изучении со­циально-экономических процессов, отражающих результаты де­ятельности фирм, предприятий и организаций (например, средняя заработная плата, производительность труда, урожайность, сред­ние темпы роста и прироста объема производства продукции или продаж, изменение себестоимости продукции).

5.2.

Виды средних величин

Существуют несколько видов средних, которые исполь­зуются в социально-экономической статистике. К их числу отно­сятся: средняя арифметическая, средняя гармоническая, средняя геометрическая, степенная средняя, средняя хронологическая, а также структурные средние — мода, медиана.

Основная задача средней величины любого вида — показать типичный уровень признака изучаемой однородной совокупно­сти при исключении влияния индивидуальных различий. Наи­более распространенным видом средних показателей в практи­ке экономических расчетов является средняя арифметическая величина. Средняя арифметическая величина рассчитывается как частное от деления суммы индивидуальных значений признака на число единиц совокупности. Средняя арифметическая вели­чина бывает простой и взвешенной.

Допустим, что заработная плата у 10 рабочих составляла в месяц (руб.): 3100, 3600, 4500, 4900, 5300, 5400, 5600, 5700, 5900, 6000. Размер заработной платы каждого из десяти рабочих зави­сит от многих факторов и является величиной индивидуальной и тем самым не может дать представления об ее уровне по всей группе рабочих. Для этого надо определить средний уровень заработной платы. Суммируем заработную плату всех рабочих и полученный итог, представляющий собой фонд заработной пла­ты, разделим на число рабочих. Это составит:

 

3100 + 3600 + 4500 + 4900 + 5300 + 5400 + 5600 + 5700 + 5900 + 6000 _

₌ 5Щ0₌ 5ооо руб.

 

Среднемесячный размер заработной платы по группе рабочих составляет 5000 руб. Это средняя арифметическая величина про­стая, поскольку исчисляется простым суммированием индиви­дуальных значений признака и делением этой суммы на число значений.

Отдельные значения признака единицы статистической сово­купности, отличные от значений его у других единиц (в нашем примере заработная плата каждого рабочего — 3100, 3600, 4500 и т.д.), в статистике принято называть вариантами и обозначать символом х_{9 где / может принимать любые значения от 1 до п. При наличии в совокупности п вариант последняя из них обозна­чается х_п. В нашем примере п = 10, таким образом, х_{ = 3100,

3600 и т.д., х₁₀= 6000. Величина средней варианты обознача­ется х, а знак суммы вариант - через S.

Расчет средней арифметической простой можно записать в виде следующей формулы:

п

- _ Х\+Х2+Хз+... + Х_п _ _i=\ (5 1)

^ар п п

Для того чтобы использовать данную формулу в Excel, необ­ходимо ввести исходные данные в таблицу, установить курсор в свободную ячейку и вызвать Мастер функций. В открывшемся диалоговом окне нужно выбрать категорию Статистические, функцию СРЗНАЧ(рис. 5.1).

Мастер функций - шаг 1 из 2

Поиск функции:

Введите краткое описание действия, которое нужно выполнить, и нажмите кнопку "Найти"

Найти

Справка по этой функции

ОК

Отмена

 

В данном примере только двое рабочих получили по 2500 руб., шесть — по 4500 руб. и т.д., т.е. индивидуальные значения зара­ботной платы рабочих повторяются неодинаковое число раз, поэтому при исчислении средней заработной платы нельзя пользоваться формулой средней арифметической простой. Для вычисления средней заработной платы 50 рабочих (см. табл. 5.1) необходимо, как и в первом случае, определить общий фонд заработной платы всех рабочих. Для этого индивидуальную за­работную плату каждой группы рабочих умножают на число ра­бочих в данной группе и полученные произведения суммируют. Затем для вычисления средней заработной платы всей совокуп­ности рабочих необходимо полученный фонд заработной платы разделить на общую численность рабочих.

 

_ _ 2500-2+4500-6+5000-12+6000-16+8000-14 _ 300000 _ ^ЛЛО ^
V" 2+6+12+16+14 " 50 -°^иииРУ°-

 

Числа, которые показывают, сколько раз (или как часто) повторяются конкретные значения признака статистической совокупности, в статистике принято называть частотами. В на­шем примере частотами являются 2; 6; 12; 16; 14. Они показыва­ют, что заработная плата 2500 руб. встречается два раза, 4500 руб. — шесть раз и т.д. Частоты еще называют весами средней, отсюда и происходит название средней взвешенной.

Расчет средней арифметической взвешенной можно выразить следующей формулой:

п

- _ + x₂f₂ + х_г/₃ +...+x_kf„ _ ,₌₁ (5.2)

Хар--------------------------------------------------------------------------, ⁴ '

 

где Xj — значение вариант; ^/=|

fi — значение весов (частот).

Таким образом, при исчислении средней арифметической взвешенной величины все варианты надо умножить на их час­тоты, тогда каждая величина х. будет участвовать в образовании средней пропорционально своему значению.

В Excel функция для расчета взвешенной средней арифме­тической в явном виде отсутствует, однако ее можно получить комбинацией функций СУММПРОИЗВ и СУММ. Функция СУММПРОИЗВ позволяет перемножить соответствующие эле­менты массивов или диапазонов и возвращает сумму произведе­ний. Функция СУММ суммирует аргументы указанного диапа­зона. Отношение этих двух функций позволяет вычислить искомое значение.

Введем исходные данные (рис. 5.2).

 

 

	А_ J........... В JL С 1 _ D J. Е_ F |
	Месячная заработная плата рабочих, руб
3 4	Число рабочих
	Среднее арифметическое взвешенное 6000

Рис. 5.2. Вид рабочего листа Ср.арифм. после ввода исходных данных В результате итоговая формула примет вид:

=CyMMnPOH3B(B2:F2;B3:F3)/CyMM(B3:F3).

Иногда среднюю арифметическую величину исчисляют по данным интервального вариационного ряда (когда варианты признака, по которому исчисляется средняя величина, представ­лены в виде интервалов «от и до»). Например, определим сред­ний размер капитальных затрат на одно хозяйство, используя данные табл. 5.2.

В таблице данные первого и последнего интервалов размера капитальных затрат являются открытыми. Для последующих расчетов необходимо определить недостающие границы этих интервалов. Граница первого интервала определяется величи­ной последующего, а последнего — величиной предыдущего. Далее необходимо вычислить середину каждого интервала.

Группировка леспромхозов по размеру капитальных затрат
\ (данные условные)

 

Размер капитальных затрат, млн руб.	Число леспромхозов
До 10
10- 12
12- 14
14- 16
16- 18
18 и более

Расчет среднего размера капитальных затрат на один леспромхоз по данным приведенного вариационного ряда (данные условные)

 

Расчет средней арифметической величины проведем на при­мере двойного интервального вариационного ряда (табл. 5.3). Первый и второй столбцы содержат исходные данные.

Далее необходимо определить середину интервала каждой группы (графа 3) и вычислить размер капитальных затрат по каждой группе леспромхозов и общий (суммарный) объем ка­питальных затрат по всем леспромхозам (графа 4).

В результате предварительных расчетов, представленных в табл. 5.3, и используя формулу (5.2) средней арифметической взвешенной, определим величину среднего размера капиталь­ных затрат в расчете на один леспромхоз.

В нашем примере средний размер капитальных затрат на один леспромхоз составит (млн руб.):

п

" -°Z°-141

2jJi i=l

Необходимо помнить, что средняя арифметическая интер­вального ряда менее точна, чем средняя арифметическая, ис­численная из конкретных вариант, потому что при исчислении середины интервалов допущена некоторая условность. Предпо­лагается, что значения признака x_i внутри интервала распреде­лены равномерно.

Средняя арифметическая величина является одним из важ­нейших обобщающих показателей изучаемых статистических совокупностей и обладает важными свойствами.

1. Сумма всех положительных и отрицательных отклонений вариант от средней арифметической равняется нулю:

п

^(jc, -1) = 0 (если частоты равны единице);

/=1

-x^fi= 0 (если частоты различны).

/=1

 

2. Сумма квадратов отклонений вариант от средней арифме­тической величины всегда меньше, чем сумма квадратов откло­нений вариант от любого другого числа:

 

i(*i-x)²<i(xi-Af

/=1 1=1

3. Если каждую варианту совокупности умножить или разде­лить на некоторое постоянное число А, то средняя арифмети­ческая увеличится или уменьшится во столько же раз:

 

& х-А или = i

п п А

 

4. Если к каждой варианте совокупности прибавить или из каж­дой варианты вычесть некоторое постоянное число А, то средняя арифметическая увеличится или уменьшится на ту же величину:

£ (*i±A)

&-------- = х±А.

 

5. Если увеличить или уменьшить частоту каждой варианты совокупности/в А раз, то величина средней арифметической не изменится:

2*/// /=i

X.

п f (п

1=1

ц

Для определения средней арифметической величины, как было показано выше, необходимо иметь значения вариант х/ и частот //. В тех случаях, когда при вычислении средней вели­чины имеются данные об индивидуальных значениях признака х и его общем объеме в совокупности W= xf, но исходная стати­стическая информация не содержит сведений о частотах /, тог­да суммированию подлежат не сами варианты, а обратные им величины. Обратной называется величина, получаемая в резуль­тате деления единицы на данное число. Для расчетов применя­ется формула средней гармонической взвешенной:

3? =&-L (5.3)

 

 

где X; — значение отдельной варианты;

T^jy. — общее число вариант, или объем выборки. /=1

8-2447 113

Рассчитать значение взвешенной средней арифметической ве­личины на примере интервального вариационного рада можно и в Excel. Используемые для этого формулы приведены на рис. 5.3. Более детально процесс вычислений представлен в приложении 7.

Если отдельные индивидуальные значения признака (вари­анты) встречаются по одному разу, то для расчетов используется формула средней гармонической простой:

 

•*тарм п ⁹ (5-4)

 

где j^_L - сумма обратных значений вариант; п — число вариант.

Рассмотрим вычисление средней гармонической величины на условном примере (табл. 5.4). Допустим, имеются данные о затратах на производство и о себестоимости единицы продук­ции А по трем заводам. Требуется определить среднюю себесто­имость единицы продукции по всем заводам в целом.

Таблица 5.4

Расчет средней гармонической величины (данные условные)

 

Номер завода	Себестоимость единицы продукции, РУб. (А)	Затраты на производство, РУб. (И*	Количество произведенной продукции, единиц
			400000: 40 = 10000
			920000: 46 = 20000
			220000: 44 = 5000
Итого	-	W= 1540000	W: ЛГ= 35000

Средняя себестоимость единицы продукции может быть вы­числена по формуле средней арифметической. Для этого необхо­димо общую сумму затрат на производство продукции разделить на количество произведенной продукции. Но если общая сумма затрат на производство продукции нам известна, то количество произведенной продукции можно определить только расчетным путем (в исходных данных эти сведения отсутствуют).

Таким образом, средняя себестоимость может быть определе­на в результате выполнения двух арифметических действий. Преж­де всего необходимо определить общее количество выработанной продукции на трех заводах. Для этого следует произведенные зат­раты на каждом заводе разделить на соответствующую себестои­мость единицы продукции и полученные результаты по каждому заводу суммировать. Затем общую сумму затрат разделить на об­щее количество произведенной продукции на всех заводах. По­лученный результат будет представлять собой среднюю себестои­мость единицы продукции по всем заводам, но тот же результат можно получить более рациональным способом.

Для этого необходимо воспользоваться формулой средней гармонической взвешенной (5.3). С этой целью среднюю себес­тоимость единицы продукции по всем заводам вычислим путем деления общей суммы затрат на общее количество произведен­ной продукции по формуле

 

 

i=i

В этой формуле числитель отражает общую сумму затрат, а знаменатель — общее количество произведенной продукции (об­ратные значения признака). Эта формула носит название сред­ней гармонической взвешенной величины.

В практике статистической обработки материала кроме сред­ней арифметической и средней гармонической применяют сред­нюю геометрическую, среднюю квадратическую и т.д.

Средняя геометрическая величина представляет собой корень /а-й степени из произведения п последовательных сомножите­лей — вариант признака:

х_геом = ц1х_ух₂-х₃-...-х_п = /|П^, <⁵-⁶>

где п — число вариант; П — знак произведения.

В практике экономических расчетов, когда исходные дан­ные представлены в виде квадратных единиц измерения, для определения среднего значения признака применяют формулу средней квадратической величины.

Средняя квадратическая взвешенная величина является квад­ратным корнем из частного от деления: в числителе — сумма произведений квадратов отдельных значений признака на их веса, а в знаменателе — сумма этих весов:

*квадр t

 

 

Ы (5.7)

4 ^п

15^Л

где x_f — значения признака наблюдаемой совокупности; ft - веса.

Средняя квадратическая простая величина вычисляется по формуле

 

I ₌Ji=l_ (5.8)

•*квадр V _п •

 

Все перечисленные средние величины относятся к так назы­ваемой степенной средней:

 

(5.9)

где х. — конкретное значение признака наблюдаемой статистической совокупности;

j - среднее значение признака; п — число единиц совокупности;

к - показатель степени, значение которого определяет вид сред­ней величины.

Таким образом, подставляя соответствующие значения по­казателя степени к, получим следующие формулы:

п

при к = 1 средняя арифметическая равна дс_ар ⁼ⁱ⁼Jp;

и

при к = 2 средняя квадратическая равна х_К = *1Ы_ при £ = 0 средняя геометрическая равна

= Hlx_rx₂-x_r...-x_n =^П^»

при £ = — 1 средняя гармоническая равна

 

ⁿ 1

*гарм ~ у '„ ~

£1

Для расчета средней гармонической взвешенной с помощью Excel введем исходные данные в виде таблицы и воспользуемся формулами, представленными на рис. 5.4.

 

	А	в.	С	D |
	Расчет средней гармонической величины (данные условные)
	Номер завода	Себестоимость единицы продукции, руб (X)	Затраты на производство, тыс. руб. (W)	Количество произ­веденной продукции, единиц (W:X)
				=СЗ/В3*1000
				=С4/В4*1000
				=С5/В5*1000
	Итого		=СУММ(СЗ:С5)	=CyMM(D3:D5)
_7_ 8	Средняя себестоимость единицы продукции (взвешенная средняя гармоническая)	=C6*1000/D6

 

Рис. 5.4. Вид рабочего листа в режиме отображения формул

 

Следует обратить внимание, что таблица включает данные в разных единицах измерения, поэтому при расчете они должны приводиться к общему виду. Например, в ячейке D3 формула примет вид: —СЗ/ВЗЧ000, а в ячейке Добудет введено -С6Ч000/ D6. Для более наглядного отображения данных для ячейки ДО с помощью команды Формат ячеек контекстного меню установим новый формат числа — Денежный. К сожалению, автоматизиро­вать расчет с помощью функции СРГАРМневозможно, посколь­ку она рассчитывает значение невзвешенной средней гармони­ческой.

Все указанные средние величины относятся к разряду пара­метрических показателей.

Рассмотренные средние величины обладают некоторыми общими свойствами. Во-первых, все указанные средние вели­чины относятся к разряду параметрических показателей, т.е. таких, по которым можно судить о параметрах генеральной со­вокупности. Во-вторых, указанные средние находятся между собой в определенных отношениях. Это объясняется тем, что величина степенных средних, рассчитанных на основе одних и тех же индивидуальных значений признака при различных зна­чениях показателя степени к, неодинакова. Чем выше показа­тель степени к, тем больше значение средней величины:

 

■^квадр ^ -*ар ^ -^геом ^ *гарм •

Это соотношение называется правилом мажорантности сред­них величин, оно впервые было сформулировано профессором А.Я. Боярским.

5.3.

Вариация признаков

Средняя величина служит одним из важнейших показа­телей статистической совокупности и представляет собой обобща­ющую характеристику вариационного ряда. Но этот показатель не позволяет выявить различия или вариацию индивидуальных зна­чений признака внутри изучаемой совокупности и тем более сопо­ставить между собой несколько совокупностей.

Вариации (колебания) могут возникнуть под влиянием раз­нообразных внешних или внутренних факторов, а также их со­вместного воздействия. Под влиянием этих факторов в процес­се статистического исследования отдельные единицы наблюдения могут существенно различаться между собой даже в пределах однородной совокупности. Например, качество произведенной продукции зависит от квалификации рабочих, качества исход­ного материала, станочного оборудования, соблюдения техно­логических режимов и т.д.

Возможны варианты, когда две статистические совокупнос­ти, отражающие один и тот же признак, имеют одинаковые сред­ние показатели, но их индивидуальные значения существенно отличаются друг от друга по степени вариации (колебания) ве­личины изучаемого признака. Индивидуальные значения изу­чаемого признака в одной совокупности могут мало отличаться друг от друга и близко группироваться вокруг средней, а в дру­гой могут наблюдаться значительные колебания относительно средней величины данного ряда.

Например, имеются сведения о дневной выручке двух мага­зинов (табл. 5.5). В каждом магазине работали пять продавцов.

Таблица 5.5 Данные о дневной выручке двух магазинов

 

Магазин	Число продавцов	Дневная выручка каждого продавца, тыс. руб.	Средняя дневная выручка одного продавца, тыс. руб.
Nq 1
№ 2

 

Средняя дневная выручка одного продавца в магазинах № 1 и 2 одинаковая и составляет 30 тыс. руб. Дневная выручка каж­дого отдельного продавца различна и, видимо, зависит от мно­гих факторов: уровня квалификации, ассортимента, места рас­положения магазина, организации рабочего места, цены товара и т.д.

На дневную выручку продавцов магазина № 2 воздействовало значительно больше разнообразных условий, чем на результаты работы продавцов магазина № 1, у которых дневная выручка близ­ко группируется вокруг среднего показателя.

Вариация свойственна практически всем без исключения при­родным и общественным явлениям и процессам. Мера вариации позволяет установить различие между значениями отдельных еди­ниц статистической совокупности и ее средним значением. Ве­личина возможных колебаний индивидуальных значений статис­

тической совокупности оценивается числовыми показателями, которые в обобщенном виде отражают особенности изучаемых распределений и позволяют сопоставлять их между собой.

В зависимости от целей и задач исследования конкретных распределений в статистике исчисляют разнообразные показа­тели вариации (рис. 5.5). К их числу можно отнести:

Показатели структуры вариации

Показатели размера вариации

• показатели структуры вариационного ряда распределения (мода, медиана, квартили, децили, перцентили);

• показатели размера вариации (размах вариации; среднее линейное отклонение; средний квадрат отклонения (дисперсия); среднее квадратическое отклонение, коэффициент вариации);

• показатели формы вариационного ряда распределения (асимметрия, эксцесс).

Показатели формы вариации

Рис. 5.5. Виды показателей вариации

Кроме средних величин для определения обобщающей ха­рактеристики ранжированного варьирующего признака изучае­мых явлений вычисляют так называемые структурные средние — моду и медиану. Средний показатель является некоторой обоб­щающей характеристикой, в то время как модальная средняя и медиана представляют собой конкретное число в наблюдаемом вариационном ряду, которое не всегда совпадает по абсолютно­му значению с расчетной величиной степенной средней.

5.4.

Показатели структуры вариации

Модой (Мо) в статистике называют величину признака, наиболее часто встречающуюся в данной совокупности. В вари­ационном ряду моду будет представлять варианта, которая об­ладает наибольшей частотой.

Показатель моды характеризует спрос, предложение, рыноч­ную цену, по которой было продано наибольшее количество товара, и т.д. Мода вычисляется только для большого объема статистической совокупности. Она может быть вычислена для несгруппированного и сгруппированного вариационного диск­ретного ряда, а также для статистических данных, представлен­ных в виде двойного интервального вариационного ряда.

Рассмотрим наиболее простой случай. Предположим, что 14.02. 2007 г. магазин продал обувь следующих размеров (табл. 5.6). Дан­ные о продаже обуви представляют собой несгруппированный диск-ретный вариационный ряд.

Таблица 5.6

Данные о продаже обуви в магазине

(уело	вные)
Дата продажи	Размер обуви	Дата продажи	Размер обуви
14.02.2007		14.02.2007
14.02.2007		14.02.2007
14.02.2007		14.02.2007
14.02.2007		14.02.2007
14.02.2007		14.02.2007
14.02.2007		14.02.2007
14.02.2007

 

Из таблицы видно, что наиболее часто встречающийся раз­мер обуви - 39.

В Excel для определения данной величины используется фун­кция МОДА (см. приложение 7). Иногда в результате расчета в ячейке отображается значение #Н/Д(нет доступного значения). Это означает, что все значения признака уникальны и не имеют повторений в пределах указанного диапазона.

Довольно часто возникают ситуации, когда исходные дан­ные представлены в таблице в упорядоченном виде. В этом слу­чае говорят о сгруппированном дискретном вариационном ряде. Если значения единиц статистической совокупности представляют собой дискретный признак, то мода определяется очень просто — по наибольшей частоте.

Например, при обследовании 500 семей рабочих одной из отраслей промышленности установлены следующие их размеры по количеству членов семей (табл. 5.7).

Таблица 5.7

Вариационный ряд

 

Количество членов семьи, чел.
Количество семей

 

Модальной величиной в данном случае будет семья, в составе которой четыре человека, так как этому значению в нашем ряду распределения соответствует наибольшее число семей — 260.

В дискретном ряду модой является варианта с наибольшей частотой. Для вычисления моды необходимо найти частоту мо­дального интервала, а затем соответствующее ему значение при­знака. Решение этой задачи в Excel показано на рис. 5.6. Детальное описание вычислений приведено в приложении 7.

В отличие от дискретных вариационных рядов вычисление моды в интервальных рядах осуществляют по следующей формуле:

Мо = *о ^{+ /}

(/Мо ~ /Мо-\) ⁺ (fMo ~ Д/о+1)

(5.10)

/ Л/о Л/о-/ Л/0+/

где х₀ — нижняя граница модального интервала (модальным является интервал, имеющий наибольшую частоту); величина модального интервала; частота модального интервала; частота интервала, предшествующего модальному; частота интервала, следующего за модальным.

Проиллюстрируем вычисление моды на следующем примере (табл. 5.8).

Таблица 5.8

Распределение по возрасту населения, занятого предпринимательской деятельностью без образования юридического лица в одном из регионов России (данные условные)

 

Возраст населения, лет	Середина интервала, лет	Население, тыс. чел.
До 20
20-25
25-30
30-35
35-40
40-45
45-50
50-55
55-60
Итого

Интервал с границами от 35 до 40 лет будет модальным, так как он имеет наибольшую частоту — 120 тыс. чел. были заняты в этом возрасте предпринимательской деятельностью без образо­вания юридического лица. Воспользуемся приведенной ранее формулой (5.10) и определим величину моды:

 

Мо = 35 + 5_______ 120-90________ = 35 + 5311 = 38

мо ^^+:>(₁₂о-90)+(120-100) ^{JD + D}50 ^

Расчетная величина моды, равная 38 годам, — это наиболее часто встречающийся возраст лиц, занятых предпринимательс­кой деятельностью без образования юридического лица в одном из регионов России.

В Excel вычисление моды по интервальному ряду выполняют по формуле (5.10). После формирования таблицы и ввода исход­ных данных выполняют расчет показателей, входящих в формулу. Промежуточные значения указывают под таблицей. Это делают для упрощения итоговой формулы и повышения наглядности. Ра­бочий лист с используемыми формулами представлен на рис. 5.7. Комментарии к вычислениям можно найти в приложении 7.

Медианой (Мё), или серединным значением наблюдаемой совокупности, в статистике называют величину варьирующего признака, которая находится в середине ряда, расположенного в порядке возрастания или убывания.

Иначе можно сказать, что медиана — это серединное значе­ние вариационного ряда. Отсюда нетрудно сформулировать ос­новное свойство медианы: сумма абсолютных отклонений зна­чений признака от медианы меньше, чем от любой другой вели­чины:

 

£1*,- -Me | = min.

Медиана, как и мода, может быть рассчитана для несгруп-пированных и сгруппированных данных дискретного вариаци­онного ряда и для исходных данных, представленных в виде двойного интервального вариационного ряда.

Пример. Допустим, что процент выполнения плана това­рооборота за месяц в 13 торговых организациях города соста­вил (%):

126,0; 98,0; 135,0; 101,0; 109,0; 115,0; 104,0; 119,0; 202,0; 144,0; 95,0; 176,0; 223,0.

Упорядочим исходный дискретный ряд по мере возрастания процента выполнения торговыми организациями плана товаро­оборота. В этом случае полученные данные выстроятся в следу­ющий ряд (%):

95,0; 98,0; 101,0; 104,0; 109,0; 115,0; 119,0; 126,0; 135,0; 144,0; 176,0; 202,0; 223,0.

Медианой здесь будет 7-я варианта, которая делит упорядо­ченный ряд пополам и соответствует 119,0% выполнения плана товарооборота.

Для определения места медианы в дискретном вариацион­ном ряду надо к сумме частот этого ряда п прибавить единицу и полученное число разделить на два:

 

n_me=*£, (5.11)

где n_me — место медианы;

п — объем совокупности (сумма частот).

Если в вариационном ряду четное число вариант, тогда ме­дианой будет половина суммы двух серединных вариант:

 

_Мс= х_Ме+х_Ме+1 (512)

 

Для вычисления медианы неупорядоченного дискретного ряда в Excel используется функция МЕДИАНА (рис. 5.8 и приложе­ние 7).

 

	А	В
	Выполнение плана товарооборота предприятиями торговли
	Номер предприятия	Процент выполнения
Л. 17;	Медиана	=МЕДИАНА(ВЗ:В16)

 

Рис. 5.8. Вид рабочего листа в режиме отображения формул

 

Медиана позволяет определить значение признака, находя­щегося в середине упорядоченной (ранжированной) совокупно­сти. Ранжирование ряда при использовании функций Excel выполняется автоматически. При нечетном числе элементов ме­дианой является варианта, расположенная в центре. При чет­ном количестве элементов вычисляется среднее значение двух центральных вариант. Например, если в ячейку В16 поместить дополнительное число 144.0, то вычисления по измененной фор­муле =МЕДИАНА(ВЗ:В16) позволит получить значение 122.5.

Вычисление медианы можно выполнить и для сгруппиро­ванных данных дискретного ряда. Определим место медианного значения признака по данным табл. 5.7. Например, если общее количество обследованных семей равно 500, то в данном случае имеем:

 

Ы_Ме=Щ±± = 250,5. (5-13)

 

При четном или нечетном числе единиц статистической со­вокупности всегда получаем конкретное место медианы, по ко­торому определяем медианное значение признака. В нашем слу­чае среднее количество человек у 250-й и 251-й семей и будет представлять собой медианное значение признака. Чтобы найти 250-ю и 251-ю семью, необходимо последовательно суммиро­вать все частоты и таким образом построить ряд накопленных частот. Для этого к 50 семьям, состоящим из двух человек, при­бавим 80 семей, состоящих из трех человек, и необходимо при­бавить еще 120 семей, чтобы вычислить численность 250-й се­мьи. Таким образом, убеждаемся, что 250-я и 251-я семьи состоят из четырех человек. Следовательно, медиана Me = 4.

В Excel задача разбивается на несколько этапов (см. прило­жение 7):

• подсчет общего числа семей;

• вычисление накопленных частот;

• поиск медианного (среднего) значения;

• определение ячейки, в которой хранится медианное зна­чение;

• выбор соответствующего этой ячейке значения из диапа­зона А2:А9.

Используемые для расчета формулы представлены на рис. 5.9. Для интервального вариационного ряда медиана вычисляет­ся по следующей формуле:

 

	А	В	С	D
	Количество	Количество семей	Накопленные
	членов семьи	частоты	t
			=В2	'|=ЕСЛИ(И[$В$12>0;$В$12<С2); 1	0)
			=С2+В3	1=ЁСЛЙ(И($В$12>С2;$В$12<СЗ)		0)
	А		=СЗ+В4	"=ЕСЛИ(И($В$12>СЗ;$В$12<С4)		0)
			=С4+В5	"=ЕСЛИ(И($В$12>С4;$В$12<С5)		0)
			=С5+В6	=ЕСЛИ(И($В$12>С5;$В$12<С6)		0)
			=Сб+В7	| =ЕСЛИ(И($В$12>С6;$В$12<С7)		0)
			=С7+В8	=ЕСЛИ(И($В$12>С7;$В$12<С8)		0)
			=С8+В9	" =ЕСЛИ(И($В$12>С8;$В$12<С9)		0)
	Общее число семей	=СУММ(В2:В9)
	Номер медианного
	значения	=В11/2
Ж	Поиск позиции	=nOMCKn63(1;D2:D9;0)
14n	Медиана	=ИНДЕКС(А2:А9;В13;1)

 

 

Рис. 5.9. Вид рабочего листа в режиме отображения формул

Me = xo+i-^—-------------, (5.14)

JMe

 

где х₀ — нижняя граница медианного интервала (медианным назы­вается первый интервал, накопленная частота которого пре­вышает половину общей суммы частот); / — величина медианного интервала;

S_Me__{ - накопленная частота интервала, предшествующего медиан­ному;

f_Me — частота медианного интервала.

Определим величину медианы для данных, приведенных в табл. 5.8. С этой целью дополним табл. 5.8 столбцом накоплен­ных частот, в результате получим табл. 5.9.

Таблица 5.9

Распределение по возрасту населения, занятого в сфере предпринимательской деятельности без образования юридического лица в одном из регионов России (данные условные)

 

Возраст населения, лет	Середина интервала, лет	Население, тыс. чел.	Накопленные частоты
До 20
20-25
25-30
30-35
35-40
40-45
45 - 50
50-55
55 - 60
Итого

---

<== предыдущая лекция | следующая лекция ==> Реакция среды растворов солей | Співвідношення та взаємодія держави і особи

Поделиться с друзьями:

---

Дата добавления: 2016-12-06; Мы поможем в написании ваших работ!; просмотров: 511 | Нарушение авторских прав

---

Лучшие изречения:

© 2015-2024 lektsii.org - Контакты - Последнее добавление