Применение счетчиков для изучения законов радиоактивного распада
Для изучения радиоактивного распада применяют счётчики Гейгера-Мюллера, пропорциональные счётчики, сцинтилляционные счётчики и др.[1,4,5]. Число отсчётов счетчика за равные промежутки времени пропорционально активности λN препарата. В силу случайности характера радиоактивного распада, определяемого формулами (1.13), (1.18) и (1.19), случайным оказывается и число импульсов, зарегистрированных за определенный интервал времени. Образовавшиеся при распаде α-,β-частицы и γ–кванты ионизируют газ, которым наполнен счетчик, или вызывают вспышки свечения в кристалле сцинтилляционного счетчика. В электронной части образуются импульсы напряжения, которые регистрируются установкой. Докажем, что вероятность появления импульсов во временном интервале от t до t+dt также определяется распределением Пуассона. При практических измерениях справедливы два приближения:
1.Число регистрируемых частиц несравненно меньше полного числа радиоактивных ядер (n<<N).
2.Время измерения мало по сравнению с периодом полураспада (λt<< 1).
Рассмотрим счетчик, регистрирующий ионизирующие частицы, попавшие в его объем. Найдем вероятность того, что при интенсивности n излучения препарата (т.е. отношения к единице площади числа отсчетов счетчика в секунду, усредненного за очень большой отрезок времени) счетчик за время измерения сработает n раз. Будем для простоты считать, что счетчик обладает единичной площадью. Окончательные формулы от этого предположения не зависят.
При вычислении вероятностей представим себе очень большое число N 1 совершенно одинаковых одновременно работающих счетчиков. За выбранный интервал времени некоторая часть их сработает n раз. Доля, составляемая этими счетчиками, по отношению к полному числу счетчиков и равна вероятности того, что через счетчик за время измерения пройдет n частиц. Через все счетчики в секунду в среднем проходит N 1 n частиц, а за небольшое время dt пройдет N 1 ndt частиц. Если dt достаточно мало, то ни через один из счетчиков за это время не пройдет двух частиц, и наши счетчики можно разбить на два класса: те, через которые за dt прошла частица, и те, через которые не прошла. Последние составляют, конечно, огромное большинство. Число счетчиков, через которые прошла частица, равно, очевидно, числу сосчитанных частиц, т.е. приблизительно N 1 ndt, а их доля по отношению к полному числу счетчиков составляет N 1 ndt /N 1 =ndt. Вероятность того, что за время dt через отдельный счетчик пройдет частица, равна, следовательно, ndt. Это утверждение справедливо только при очень малом отрезке dt.
Вычислим вероятность P 0(t) того, что за время t через счетчик не пройдет ни одной частицы. По определению число таких счетчиков в момент t составляет N 1 P 0(t), а в момент t+ dt равно N 1 P 0(t+dt), причем N 1 P 0(t+dt)< N 1 P 0(t), так как за время dt число таких счетчиков убавится на N 1 P 0(t)ndt, поэтому
N 1 P 0(t+dt) = N 1 P 0(t) – N 1 P 0(t)ndt,
или
P 0(t+dt) - P 0(t) = - P 0(t)ndt.
Отсюда получим уравнение
dP 0/ dt = -n P 0,
интегрируя которое, получим
P 0(t) = е-n t . (2.1)
При интегрировании было принято во внимание, что в начальный момент времени вероятность найти счетчик, не сработавший ни разу, равна, конечно, единице.
Вычислим теперь Pn (t+dt) – вероятность того, что за время t+dt через отдельный счетчик пройдет ровно n частиц. Эти счетчики делятся на две группы. К первой принадлежат те, через которые все n частиц прошли за время t, а за время dt не прошло ни одной. Ко второй группе принадлежат счетчики, чарез которые за время t прошла n -1 частица, а последняя частица прошла за время dt. Число первых счетчиков равно N 1 P n(t)(1-n dt), а число вторых составляет N 1 Pn- 1(t)n dt. Каждое из этих выражений состоит из двух сомножителей. Первый из них определяет вероятность нужного числа срабатываний за время t, а второй – вероятность несрабатывания или срабатывания за время dt. Имеем, следовательно,
N 1 Pn (t+dt)= N 1 Pn (t)(1-n dt)+ N 1 Pn- 1(t)n dt.
Перенесем первое слагаемое справа в левую часть, разделим обе части на N 1 dt и, перейдя к пределу при dt ®0, получим
dPn /dt + nPn= n Pn -1.
Последовательно применяя полученную рекурентную формулу к n= 1, n =2 и т. д. с помощью (2.1) найдем
 (2.2)
(2.2)
Заметим теперь, что n t, которое мы обозначим через n 0, равно среднему числу частиц, проходящих через счетчик за время t. Формула (2.2) примет вид
 (2.3)
(2.3)
Эта формула является окончательной и носит название распределения Пуассона с математическим ожиданием п 0. Она в нашем случае определяет вероятность того, что при среднем числе срабатываний n 0 (это число, вообще говоря, не является целым) произойдет именно n срабатываний (n – целое число).
Поскольку с помощью счетчиков регистрируется число импульсов, пропорциональное числу распавшихся ядер за определенный интервал времени, то не удивительно, что характер распределения импульсов такой же, а формулы (1.9) и (2.3) определяют пуассоновский характер распределения.
Из всех характеристик работы счетчика осталась одна – среднее число срабатываний за время измерения, которое можно выбрать произвольно. Площадь поперечного сечения счетчика, которую мы для простоты положили равной единице, также не входит в окончательный результат.
Рассмотрим некоторые свойства формулы (2.3). Вычислим, прежде всего, вероятность найти какое угодно значение n:

Этот результат является очевидным, т.к. мы вычислили вероятность достоверного события.
Хоть какое-нибудь значение n, конечно, всегда будет найдено на опыте.
Для дискретного распределения среднее значение n вычисляется по формуле (1.12)
 (2.4)
(2.4)
где s=n- 1 [2,3]. Как и следовало ожидать, среднее число импульсов соответствует максимуму в распределении Pn (n 0). Сравните этот результат с формулой (1.13). Было уже доказано [см. формулы (1.15) – (1.17)] а также [6], что дисперсия
 (2.5)
(2.5)
а стандартная (среднеквадратичная) ошибка (СКО) по определению
 (2.6)
(2.6)
Если в некотором интервале t число импульсов п подсчитывается один раз, то с вероятностью, составляющей»70%, можно утверждать, что среднее значение n 0 находится в интервале от 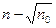 до
до  [5].
[5].
Истинное среднее значение измеряемой величины неизвестно, поэтому по этому в формулу для определения стандартной ошибки отдельного измерения приходится подставлять не истинное среднее значение п 0, а измеренное значение п
 , (2.7)
, (2.7)
а результат определения среднего значения записывать так [5]
 . (2.8)
. (2.8)
Обычно пользуются понятием скорости счета и определяют число импульсов в минуту. Если измерение проводят t минут (время измеряется без погрешности),то, поделив (2.7 на время и обозначив скорость счета буквой J, получим
 . (2.8)
. (2.8)
Среднюю квадратическую ошибку можно уменьшить, проведя серию измерений числа импульсов за интервал времени t, получив выборку из К значений. К равно количеству попыток измерения скорости счета. Методом максимального правдоподобия [4] доказано, что
 , (2.9)
, (2.9)
дисперсия уменьшится в К раз, а результат следует записывать в виде
 . (2.10)
. (2.10)
Ошибка определения наиболее вероятной (средней) скорости счета уменьшается обратно пропорционально корню квадратному из числа К измерений.
Если некоторая величина y является функцией нескольких независимых переменных y=y (x 1 ,x 2 ,…,xm), определяемых с погрешностями D x 1, D x 2,…,D xm, то ошибку зависимой переменной находят по формуле [5]
 . (2.11)
. (2.11)
В предположении идеальности измерения времени без учета фона скорость счета импульсов определяется по формуле JA=n/t и в соответствии с (2.11) при относительно малых D n имеем
 . (2.12)
. (2.12)
Относительная ошибка равна
 . (2.13)
. (2.13)
Как видно, эта ошибка уменьшается обратно пропорционально корню квадратному от времени, в течение которого определялась скорость счета.
При измерениях JA часто необходимо учитывать фон. Регистрируется суммарное воздействие на счетчик фона и радиоактивного препарата и только фона JA+Ф и JФ соответственно. Скорость счета от препарата представляет собой разность JА+Ф-JФ, поэтому [5]
 . (2.14)
. (2.14)
При выполнении измерений возникает задача наилучшего распределения некоторого заданного времени T=tА+Ф+tФ между tА+Ф и tФ для того, чтобы ошибка D JA была минимальной, то-есть
 =0.
=0.
Отсюда имеем
 ,
,
или
 . (2.15)
. (2.15)
С учетом фона относительную ошибку измерения скорости счета при измерении активности препарата определяют по формуле
 (2.16)
(2.16)
Откуда
 . (2.17)
. (2.17)






