Компьютерные технологии статистического прогнозирования (2 ч.)
Цель работы: Изучение метода регрессионного анализа с использованием табличного процессора Microsoft Excel.
Содержание отчета:
1. Тема лабораторной работы.
2. Цель работы.
3. Порядок выполнения работы.
4. Ответы на контрольные вопросы.
Построение парной регрессии при помощи линий тренда
Если изменение значений объекта исследования y связано со временем t, то такой случайный процесс y (t) называется временным рядом, а построенная регрессионная модель – линией тренда: 
.
Пример 1. Требуется оценить величину спроса на товар фирмы на следующие два месяца (июль и август 2013 г.). В качестве исходных данных взята динамика изменения спроса за последние 18 месяцев (рис. 1, блок ячеек А1:С19).
Решение: Прогнозирование спроса будем осуществлять по математической модели в виде уравнения регрессии. При этом на первом этапе, в качестве первого приближения выберем линейную модель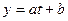 
(здесь t – регрессионная переменная).
I этап. Линейная аппроксимация.
Шаг 1. Ввести исходные данные (диапазон А1:С19).
Шаг 2. Вызвать мастер диаграмм (Вставка / Диаграмма).
Шаг 3. В открывшемся окне Тип диаграммы выбрать тип Точечная. Выбрать 1-й тип в виде отдельных точек.
Шаг 4. В окне Источник данных диаграммы ввести диапазон $B$2:$C$19.
Шаг 5. В окне Параметры диаграммы ввести название диаграммы «Линейная модель», осей X, Y и убрать легенду. В окне Размещение диаграммы нажать кнопку Готово.
Шаг 6. Нажать правой кнопкой мыши на одну из точек диаграммы. В появившемся меню выбрать пункт Добавить линию тренда. В окне Линия тренда на вкладке Тип выбрать Линейная; на вкладке Параметры поставить флажки:
Показать уравнение на диаграмме,
Поместить на диаграмму величину достоверности аппроксимации (R^2).
На диаграмме «Линейная модель» будет выведен график 
и 
.
Шаг 7. Вывод: данным уравнением пользоваться нельзя, т.к. коэффициент детерминации 
. Для того, чтобы выяснить, какие изменения необходимо внести в модель, проведем анализ остатков.
Шаг 8. Вывод остатков. В ячейку D2 введем формулу =35,019*В2-117,12 и скопируем протягиванием от D2 до D19. Получим, что в ячейках D2:D19 вычислены значения отклика y по уравнению регрессии. В ячейку Е2 введем формулу =С2-D2. Далее копируем формулу протягиванием от ячейки Е2 до Е19, получаем столбец остатков. При помощи Мастера диаграмм строим «график остатков». При этом в качестве исходных данных по оси Х следует брать ячейки В2:В19 (для этого в Мастере диаграмм на шаге 2: «источник данных диаграммы» на вкладке Ряд нажмите кнопку Добавить и вводите данные).
Рис. 1. Линейная регрессия
Шаг 9. Анализ остатков. По виду расположения точек на графике остатков, делаем заключение: необходимо в модель добавить квадратичный член, т.е. искать зависимость в виде: 
.
