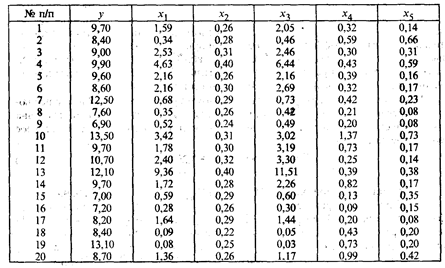
Решение. С целью предварительного анализа взаимосвязи показателей построена матрица R — таблица парных коэффициентов корреляции.
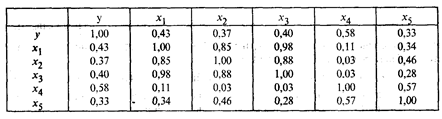
Анализ матрицы парных коэффициентов корреляции показывает, что результативный признак наиболее тесно связан с показателем х4 — количеством удобрений, расходуемых на гектар (ryx4 = 0,58).
В то же время связь между аргументами достаточно тесная. Так, существует практически функциональная связь между числом колесных тракторов (x1) и числом орудий поверхностной обработки почвы x3 (rx1x3) = 0,98.
О наличии мультиколлинеарности свидетельствуют также коэффициенты корреляции rx1x2 = 0,85 и rx3x2 = 0,88.
Чтобы продемонстрировать отрицательное влияние мультиколлинеарности, рассмотрим рассчитанное на ЭВМ регрессионное уравнение урожайности, включив в него все исходные показатели:
= 3,515 – 0,006 x1 + 15,542 x2 + 110 x3 + 4,475 х4 - 2,932 x5. (53.22)
(-0,01) (0,72) (0,13) (2,90) (-0,95)
В скобках указаны t набл (β j) = tj — расчетные значения t -критерия для проверки гипотезы о значимости коэффициента регрессии Н0: β j = 0, j = 1, 2, 3, 4, 5. Критическое значение t кр = 1,76 найдено по таблице t -распределения при уровне значимости α = 0,1 и числестепеней свободы v = 14.Из уравнения следует, что статистически значимым является коэффициент регрессии только при х4, так как | t4 | = 2,90 > t кр = 1,76. Не поддаются экономической интерпретации отрицательные значения коэффициентов регрессии при х1 и x5, из чего следует, что повышение насыщенности сельского хозяйства колесными тракторами (х1) и средствами оздоровления растений (x5) отрицательно сказывается на урожайности. Таким образом, полученное уравнение регрессии неприемлемо.
После реализации алгоритма пошагового регрессионного анализа с исключением переменных и учетом того, что в уравнение должна войти только одна из трех тесно связанных переменных (x1, х2 или x3), получаем окончательное уравнение регрессии
= 7,342 + 0,345 x1 + 3,294 x4. (53.23)
(11,12) (2,09) (3,02)
Уравнение значимо при α = 0,05, так как F набл = 266 > F кр = 3,20, найденного по таблице F -распределения при α = 0,05, v 1 = 3 и v 2 = 17. Значимы и коэффициенты регрессии β1 и β4, так как |tj| > t кр = 2,11 (при α = 0,05, v = 17). Коэффициент регрессии β1 следует признать значимым (β1 ≠ 0) из экономических соображений; при этом t1 = 2,09 лишь незначительно меньше t кр = 2,11. В случае если α = 0, 1, t кр = 1,74 и коэффициент регрессии β1 статистически значим.
Из уравнения регрессии следует, что увеличение на единицу числа тракторов на 100 га пашни приводит к росту урожайности зерновых в среднемна0,345 ц/га (b1 = 0,345).
Коэффициенты эластичности Э1 = 0,068 и Э4 = 0,161 (Э j =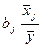 
) показывают, что при увеличении показателей x1 и х4 на 1% урожайность зерновых повышается соответственно на 0,068% и 0,161%.
Множественный коэффициент детерминации r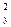 
= 0,469 свидетельствует о том, что только 46,9% вариации урожайности объясняется вошедними в модель показателями (x1 и x4), т.е. насыщенностью растениеводства тракторами и удобрениями. Остальная часть вариации обусловлена действием неучтенных факторов (х2, x3, х5, погодными условиями и др.). Средняя относительная ошибка аппроксимации 
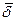= 10,5% свидетельствует об адекватности модели, так же как и величина остаточной дисперсии s2 = 1,97.
Компонентный анализ
Компонентный анализ предназначен для преобразования системы k исходных признаков в систему k новых показателей (главных компонент). Главные компоненты не коррелированы между собой и упорядочены по величине их дисперсий, причем первая главная компонента имеет наибольшую дисперсию, а последняя, k- я — наименьшую. При этом выявляются неявные, непосредственно не измеряемые, но объективно существующие закономерности, обусловленные действием как внутренних, так и внешних причин.
Компонентный анализ является одним из основных методов факторного анализа. В задачах снижения размерности и классификации обычно используются т первых компонент (т << k).
При наличии результативного признака у может быть построено уравнение регрессии на главных компонентах.
На основании матрицы исходных данных
размерности п х k, где хij.— значение j -го показателя у i -го наблюдения (i = 1, 2,..., n; j = 1, 2,.... k), вычисляют средние значения показателей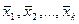 
а также s1,..., sk и матрицу нормированных значений
с элементами
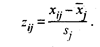
Рассчитывается матрица парных коэффициентов корреляции:
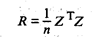(53.24)
с элементами
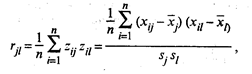(53.25)
где j, l= 1, 2, .... k.
На главной диагонали матрицы R, т.е. при j = l, расположены элементы
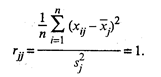
Модель компонентного анализа имеет вид
(53.26)
где aiv — «вес», т.е. факторная нагрузка v -й главной компоненты на j -ю переменную;
f iv — значение v -й главной компоненты для i -го наблюдения (объекта), где v = 1, 2, ...,k.
В матричной форме модель (53.26) имеет вид
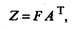(53.27)
f iv — значение v -й главной компоненты для i -го наблюдения (объекта);
aiv — значение факторной нагрузки v -й главной компоненты на j -ю переменную.
Матрица F описывает п наблюдений в пространстве k главных компонент. При этом элементы матрицы F нормированы, т.е. fv =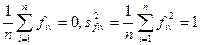 
, a главные компоненты не коррелированы между собой. Из этого следует, что
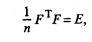(53.28)
Выражение (53.28) может быть представлено в виде
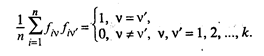(53.29)
С целью интерпретации элементов матрицы А рассмотрим выражение для парного коэффициента корреляции между переменной zj и, например, f1 -й главной компонентой. Так как zо и f1 нормированы, будем иметь с учетом (53.26):
Принимая во внимание (53.29), окончательно получим
Рассуждая аналогично, можно записать в общем виде
(53.30)
для всех j = 1, 2,.,., k и v = 1, 2,.... k.
Таким образом, элемент ajv матрицы факторных нагрузок А характеризует тесноту линейной связи между исходной переменной zj и главной компонентой fv, т.е. –1 ≤ ajv ≤ +1.
Рассмотрим теперь выражение для дисперсии нормированной переменной zj. С учетом (53.26) будем иметь
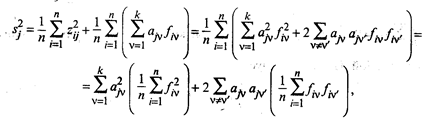
где v, v' = 1, 2,..., k.
Учитывая (53.29), окончательно получим
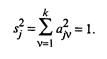(53.31)
По условию, переменные zj нормированы и s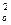 
= 1. Таким образом, дисперсия переменной zj, согласно (53.31), представлена своими составляющими, определяющими долю вклада в нее всех k главных компонент.
Полный вклад v -й главной компоненты в дисперсию всех k исходных признаков вычисляется по формуле
(53.32)
Одно из основополагающих условий метода главных компонент связано с представлением корреляционной матрицы R через матрицу факторных нагрузок А. Подставив для этого (53.27) в (53.24), будем иметь
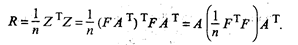
Учитывая (53.28), окончательно получим
(53.33)
Перейдем теперь непосредственно к отысканию собственных значений и собственных векторов корреляционной матрицы R.
Из линейной алгебры известно, что для любой симметричной матрицы R всегда существует такая ортогональная матрица U, что выполняется условие
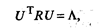(53.34)
Так как матрица R положительно определена, т.е. ее главные миноры положительны, то все собственные значения λ v > 0 для любых v =1, 2,..., k.
В компонентном анализе элементы матрицы Λ ранжированы: λ 1 ≥ λ 2 ≥ ... ≥λ v... ≥ λ k ≥ 0. Как будет показано ниже, собственное значение λ v характеризует вклад v -й главной компоненты в суммарную дисперсию исходного признакового пространства.
Таким образом, первая главная компонента вносит наибольший вклад в суммарную дисперсию, а последняя, k- я, — наименьший.
В ортогональной матрице U собственных векторов v -й столбец является собственным вектором, соответствующим λ v -му значению.
Собственные значения λ 1 ≥... ≥ λ v.... ≥λ k находятся как корни характеристического уравнения
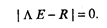(53.35)
Собственный вектор Vv, соответствующий собственному значению λ v корреляционной матрицы R, определяется как отличное от нуля решение уравнения, которое следует из (53.34):
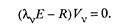(53.36)
Нормированный собственный вектор Uv равен
Из условия ортогональности матрицы U следует, что U-1 = UT, но тогда, по определению, матрицы R и Λ подобны, так как они, согласно (53.34), удовлетворяют условию
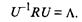
Так как у подобных матриц суммы диагональных элементов равны, то
Учитывая, что сумма диагональных элементов матрицы R равна k, будем иметь
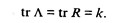
Таким образом,
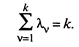(53.37)
Представим матрицу факторных нагрузок А в виде
(53.38)
а v -й столбец матрицы А — как
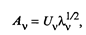
где Uv — собственный вектор матрицы R, соответствующий собственному значению λ v.
Найдем норму вектора Аv:
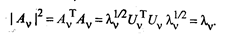(53.39)
Здесь учитывалось, что вектор Uv — нормированный и U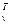 
Uv = 1. Таким образом,
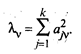
Сравнив полученный результат с (53.32), можно сделать вывод, что собственное значение λ v характеризует вклад v -й главной компоненты в суммарную дисперсию всех исходных признаков. Из (53.38) следует, что
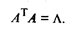(53.40)
Согласно (53.37), общий вклад всех главных компонент в суммарную дисперсию равен k. Тогда удельный вклад v -й главной компоненты определяется по формуле 
.
Суммарный вклад т первых главных компонент определяется из выражения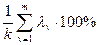 
.
Обычно для анализа используют т первых главных компонент, вклад которых в суммарную дисперсию превышает 60—70%.
Матрица факторных нагрузок А используется для экономической интерпретации главных компонент, которые представляют собой линейные функции исходных признаков. Для экономической интерпретации f v используются лишь те хj, для которых |a jv | > 0,5.
Значения главных компонент для каждого i -го объекта (i = 1, 2,.... n) задаются матрицей F.
Матрицу значений главных компонент можно получить из формулы
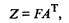
откуда
Уравнение регрессии на главных компонентах строится по алгоритму пошагового регрессионного анализа, где в качестве аргументов используются главные компоненты, а не исходные показатели. К достоинству последней модели следует отнести тот факт, что главные компоненты не коррелированы. При построении уравнений регрессии следует учитывать все главные компоненты.
Пример. Построение регрессионного уравнения
По данным примера из § 53.2 провести компонентный анализ и построить уравнение регрессии урожайности Y на главных компонентах.
Решение. В примере из § 53.2 пошаговая процедура регрессионного анализа позволила исключить отрицательное значение мультиколлинеарности на качество регрессионной модели за счет значительной потери информации. Из пяти исходных показателей в окончательную модель вошли только два (x1 и x4). Более рациональным в условиях мультиколлинеарности можно считать построение уравнения регрессии на главных компонентах, которые являются линейными функциями всех исходных показателей и не коррелированы между собой.
Воспользовавшись методом главных компонент, найдем собственные значения и на их основе — вклад главных компонент в суммарную дисперсию исходных показателей x1, х2, х3, х4, х5 (табл. 53.2).
Таблица 53.2
