Статистическая функция распределения

ТЕОРИЯ ВЕРОЯТНОСТЕЙ. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА И СЛУЧАЙНЫЕ ПРОЦЕССЫ

Контрольная работа

Оценка параметров функции распределения и построение гистограммы по опытным данным

Методические указания

Направление подготовки: 230100 - Информатика и вычислительная техника;

220200 - Автоматизация и управление

Форма обучения :за очная

Тула 2008

Цель и задачи работы

Научить пользоваться методами математической статистики: оценкой параметров распределения случайных величин, построению гистограммы распределения по опытным данным и др.

Теоретические сведения

Статистическая функция распределения

Предположим, что изучается некоторая случайная величина Х, закон распределения которой в точности неизвестен, и требуется определить этот закон из опыта или проверить экспериментально гипотезу о том, что величина Х подчинена тому или иному закону. С этой целью над случайной величиной Х производятся ряд независимых опытов (наблюдений). В каждом из этих опытов величина Х принимает определенное значение. Совокупность наблюдённых значений величины и представляет собой первичный статистический материал, подлежащий обработке, осмыслению и анализу. Такая совокупность называется «простой статистической совокупностью» или «простым статистическим рядом». В литературе используется так же термин «выборка», имея ввиду, что из генеральной совокупности объектов берется выборка из нескольких объектов и над ними производятся соответствующие испытания или измерения. Обычно простая статистическая совокупность оформляется в виде таблицы с одним входом, в первом столбце которой стоит номер опыта i, а во втором — наблюдённое значение случайной величины.

Пример 1. Случайная величина T - время восстановления отказа станка. Восстановлено 10 отказов, при восстановлении каждого из них затрачено T_i минут времени. Результаты наблюдений сведены в простой статистический ряд.

Табл.2.1.

Простой статистический ряд

	i
T_i_,мин

Простой статистический ряд представляет собой первичную форму записи статистического материала и может быть обработан различными способами. Одним из способов такой обработки является построение статистической функции распределения случайной величины.

Статистической функцией распределения случайной величины T называется частота события T<t в данном статистическом материале. То есть

Для того чтобы найти значение статистической функции распределения при данном t, достаточно подсчитать число опытов, в которых величина T приняла значение, меньшее чем t, и разделить на общее число N произведенных опытов. То есть

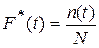где n(t)- число опытов, в которых T<t.

Для построения графика 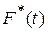опытные данные располагают в возрастающем порядке, то есть

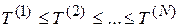Такой упорядоченный ряд статистических данных называется вариационным рядом. - наименьшее значение, 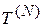- наибольшее значение,

размах выборки.

Пример 2. Построим статистическую функцию распределения для случайной величины T из предыдущего примера.

Табл.2.2

Вариационный ряд

i
T⁽ⁱ⁾

Размах выборки R =300-15=285 мин

Рис.2.1.График статистической функции распределения